※本記事はアフィリエイト広告を含んでいます

どーも、りけーこっとんです。
DS検定の勉強をしよう!と思ったは良いものの、こんな悩みはありませんか?

DS検定ってどうやって勉強すればいいの?
DS検定の勉強の仕方が分からない…

本で勉強するのは分かるけど、高いなぁ…
無料で単語解説されているサイトとかないかな?

DS検定は、始まったばかりの試験だから、対策法とか分からないよね。
じゃあ、このサイトで出題範囲の内容を押さえていこう~
DS検定の解説をすぐ見たいよ!という方は、以下から最初の解説に飛べます。


今回はスキルチェックリスト
「DS8:名義・順序・間隔・比例尺度の違いを説明できる」
「DS9:ピアソンの相関係数の分母・分子を説明できる」
「DS12:量的・質的変数の関係の強さを算出できる」を解説していくよ~
本サイトでは超重要項目、重要項目、覚えておきたい項目と表記を分けますので、勉強時の参考にしてみてください。
DS検定って、そもそもどんな資格?という方は以下の記事をご覧くださいね。
試験範囲は以下の二つから出題されます。
・スキルチェックリスト
・数理、データサイエンス、AI(リテラシーレベル)モデルカリキュラム
本内容は以下の書籍を参考に作成しております。
なお、本サイトはDS検定の合格を保証するわけではありませんので、ご了承ください。
では早速、内容に入っていきましょう!
※「DS○○:」項目の文章は独自に短縮して表現しております
DS8:名義・順序・間隔・比例尺度の違いを説明できる
この項目は以下の四つを説明できてくださいね、という項目。
●質的変数の尺度
・名義尺度
・順序尺度
●量的変数の尺度
・間隔尺度
・比例尺度
まず「質的変数」「量的変数」の説明からしていきましょう。
質的変数:
種類や分類などを分けるためにラベル付けした変数のこと。
(例)
・都道府県名(東京都、大阪府、神奈川県)
・交通手段(電車、車、自転車)
・食べ物(中華料理、カレー、かつ丼)
・ランキング(1位・2位・3位)
・学校の成績(5段階評価)
量的変数:
数値として意味があり、+-や平均値などの計算ができる変数のこと。
(例)
・温度
・偏差値
・身長
・速度
・売上
ではまず、質的変数を扱う「名義尺度」「順序尺度」から解説します。
名義尺度
名義尺度は、質的変数におけるデータの種類の1つです。
名義尺度:
データにラベルや名前を付ける質的変数の尺度のこと。
(例)
・通勤手段は?
⇒電車、車、バス、自転車、徒歩
・好きな食べ物は?
⇒カレー、かつ丼、ラーメン、オムライス
例を見ると分かりますが、数値的な意味はありません。
あくまでも「種類」や「分類」を区別するために、名前を付けたデータというイメージです。
順序尺度
順序尺度も、質的変数におけるデータの種類の1つですね。
順序尺度:
順序に意味がある質的変数の尺度のこと。
(例)
・満足度調査(5:大変満足 ~ 1:非常に不満)
・学校の成績(5:非常に優秀 ~ 1:修了不足)
・3社の人気ランキング(1位・2位・3位)
満足度調査は5の方が良いし、ランキングは1の方が良いです。
名義尺度と違って、順序に意味がありますよね。
ただし、ランキングで「1位と2位を足したら、3位になる」は意味が分かりません。
+-や平均値などの計算に意味は無いので、質的変数の尺度ということになっているんですね。
次に、量的変数を扱う「間隔尺度」「比例尺度」から解説します。
間隔尺度
間隔尺度も、量的変数におけるデータの種類の1つですね。
こちらが一番理解しにくいかもしれません。
間隔尺度:
間隔(数値の差)のみに意味がある量的変数の尺度。数字同士の比には意味がない。
(例)偏差値、温度、西暦
例えば西暦が「10年⇒15年」と「2020年⇒2025年」の時間が経過した場合を考えてみましょう。
「比」に意味があるとなると、以下のような解釈ができます。
\(\displaystyle \frac{15}{10} = 1.5\)
\(\displaystyle \frac{2025}{2020} = 1.002\)
つまり、「10年⇒15年」は10年から1.5倍、
「2020年⇒2025年」は2020年から1.002倍になっている!
5年という時間は、どちらも同じはずなのに「比」にすると意味が変わってしまいました。
西暦の場合、
\(\displaystyle 15 – 10 = 5\)
\(\displaystyle 2025 – 2020 = 5\)
のように「差」には意味がありますが、前述の通り「比」には意味がありません。
DS検定においては、間隔尺度の具体例を覚えておけば問題ないかと。
比例尺度
比例尺度も、量的変数におけるデータの種類の1つですね。
比例尺度:
一般的に想像する数字の尺度。基本的に+-×÷などの全ての計算が行える。
(例)身長、体重、速度、売上
比例尺度は、基本的にどんな計算でも行えます。
間隔尺度との違いを分かりやすくするため、例えば売上の比で考えてみましょう。
「500円⇒1000円」と「10000円⇒10500円」に売上が増加した場合
\(\displaystyle \frac{1000}{500} = 2\)
\(\displaystyle \frac{10500}{10000} = 1.05\)
つまり、「500円⇒1000円」は500円から2倍、
「10000円⇒10500円」は10000円から1.05倍になっている!
これには意味がありますよね。
同じ500円でも「10000円⇒10500円」の売上への影響は小さい、と判断しても大丈夫そうです。
尺度の種類をまとめると以下の通り。

DS9:ピアソンの相関係数の分母・分子を説明できる
ピアソンの相関係数って聞いたことありますかね?
一般的に言われている相関係数のことです。
ピアソンの相関係数:
2変数間に相関関係があるかどうかを1 ~ -1の範囲で数値化できる指標のこと。\(\displaystyle r\)
・1に近いとき ⇒ xが大きくなれば、yも大きくなる(正の相関がある)
・0に近いとき ⇒ xとyに関係はない(無相関)
・-1に近いとき ⇒ xが小さくなれば、yも小さくなる(負の相関がある)
2変数x、yの共分散を用いると
$$r = \frac{xとyの共分散}{(xの標準偏差)\times(yの標準偏差)}$$ここで、共分散についても解説しておきます。
共分散:
2変数(x, y)のデータの間に、どんな関係があるかを表す指標のこと。
共分散では以下のようなことが分かる。
・正(+)に大きいとき ⇒ xが大きくなれば、yも大きくなる(正の相関がある)
・0に近いとき ⇒ xとyに関係はない(無相関)
・負(-)に大きいとき ⇒ xが小さくなれば、yも小さくなる(負の相関がある)
共分散だけでも、ざっくりとしたデータの傾向はつかめるんですね。
その共分散を「xの標準偏差」「yの標準偏差」で割ることで、どんなデータでも1 ~ -1の範囲になります。
つまり相関係数の方が、使い勝手は良いと言えますね。
DS12:量的・質的変数の関係の強さを算出できる
関係の強さを算出できる値というのは、この記事で既に触れています。
「相関係数」でした。
ただし、相関を知りたい変数が「量的」か「質的」かで使う相関係数が変わるのです。
ピアソンの積率相関
ピアソンの積率相関とは、DS9でも触れた「ピアソンの相関係数」と同じです。
複数ある良い方も覚えておくと、DS検定合格にグッと近づけるかと思います。
ピアソンの積率相関は、量的変数に対して用いられる相関係数。
ピアソンの積率相関:\(\displaystyle r\)
2つの量的変数間に相関関係があるかどうかを1 ~ -1の範囲で数値化できる指標のこと。
・1に近いとき ⇒ xが大きくなれば、yも大きくなる(正の相関がある)
・0に近いとき ⇒ xとyに関係はない(無相関)
・-1に近いとき ⇒ xが小さくなれば、yも小さくなる(負の相関がある)
2変数x、yの共分散を用いると
$$r = \frac{xとyの共分散}{(xの標準偏差)\times(yの標準偏差)}$$具体例で、計算してみましょう。
A~E君の身長と体重で相関係数を算出したいと思います。
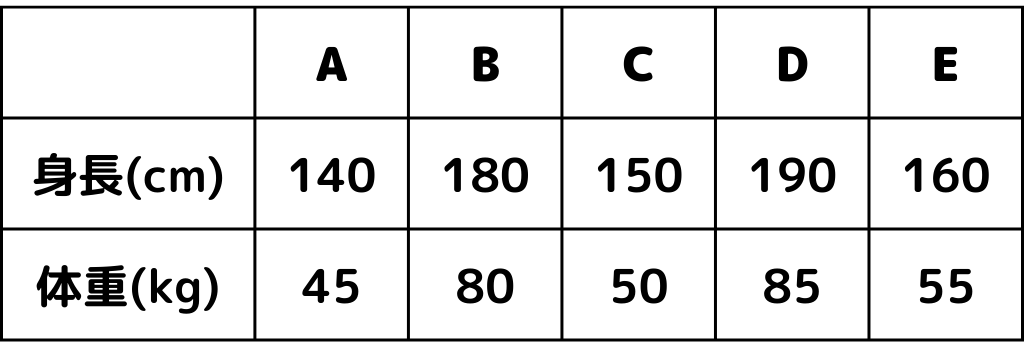
相関係数の算出に必要なのは、「2変数それぞれの平均値」「データ数」です。
身長と体重それぞれの平均値は
$$身長の平均 = \frac{140+180+150+190+160}{5} = 164$$ $$体重の平均 = \frac{45+80+50+85+55}{5} = 63$$では共分散を求めていきましょう。
$$共分散 = \frac{(140-164)\times(45-63) + (180-164)\times(80-63) + (150-164)\times(50-63) + (190-164)\times(85-63) + (160-164)\times(55-63)}{5} = \frac{(-24)\times(-18) + (16)\times(17) + (-14)\times(-13) + (26)\times(22) + (-4)\times(-8)}{5} = 346$$次に身長と体重の標準偏差を求めます。
$$身長の標準偏差 = \sqrt{\frac{(140-164)^2 + (180-164)^2 + (150-164)^2 + (190-164)^2 + (160-164)^2}{5}} = \sqrt{\frac{(-24)^2 + (16)^2 + (-14)^2 + (26)^2 + (-4)^2}{5}} = 18.547…$$ $$体重の標準偏差 = \sqrt{\frac{(45-63)^2 + (80-63)^2 + (50-63)^2 + (85-63)^2 + (55-63)^2}{5}} = \sqrt{\frac{(-18)^2 + (17)^2 + (-13)^2 + (22)^2 + (-8)^2}{5}} = 36.46…$$よって相関係数\(\displaystyle r\)は
$$r = \frac{xとyの共分散}{(xの標準偏差)×(yの標準偏差)} = \frac{346}{18.5 \times 36.5} = 0.512$$よって、0.5の正の相関があることが分かりました。
では変数同士が「質的変数」だった場合、どうなるのでしょうか。

スピアマンの順位相関
スピアマンの順位相関とは、質的変数に対して用いられる相関係数。
スピアマンの相関係数:\(\displaystyle \rho\)
2つの質的変数間に相関関係があるかどうかを1 ~ -1の範囲で数値化できる指標のこと。
・1に近いとき ⇒ xが大きくなれば、yも大きくなる(正の相関がある)
・0に近いとき ⇒ xとyに関係はない(無相関)
・-1に近いとき ⇒ xが小さくなれば、yも小さくなる(負の相関がある)
データ数を\(\displaystyle n\)、質的変数の差を\(\displaystyle d_k\)とすると
\(\displaystyle \rho = 1-\frac{6\sum_{k=1}^{n}(d_k)^2}{n(n^2 – 1)}\)
式が難しくなった気がしますよね。
こちらも具体例で計算してみましょう。
2つの会社に対するA~Eさんの満足度調査(5段階評価)をもとに、相関係数を算出したいと思います。
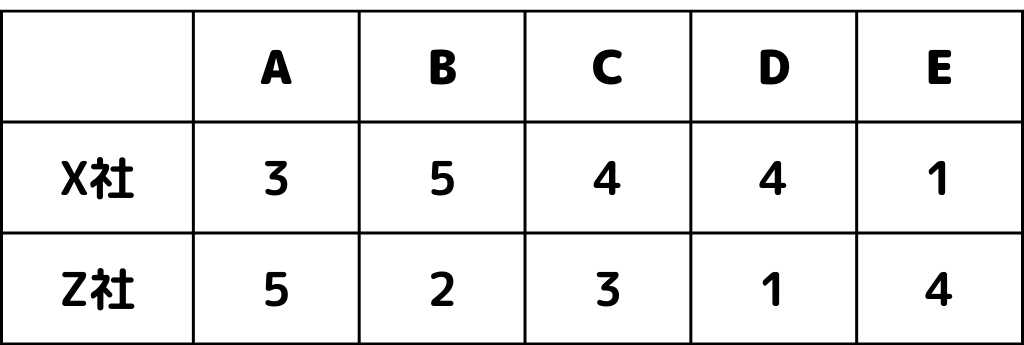
まずX社とZ社の「5段階評価の差の二乗」を合計していきましょう。
$$\sum_{k=1}^{n}(d_k)^2 = (3-5)^2 + (5-2)^2 + (4-3)^2 + (4-1)^2 + (1-4)^2 = 32$$次にnはデータ数(5個)として、定義式に代入します。
$$\rho = 1-\frac{6\sum_{k=1}^{n}(d_k)^2}{n(n^2 – 1)} = 1-\frac{6\times 32}{5(5^2 – 1)} = -0.4$$よって0.4の負の相関があることが分かりました。
まとめ
今回は「尺度の種類・相関係数」などを解説してきました。
以下の項目を説明できるようになっているでしょうか?
・名義尺度
・順序尺度
・間隔尺度
・比例尺度
・ピアソンの相関係数(積率相関)
・スピアマンの順位相関
DS検定は覚える内容が多いです。
一つ一つを細部まで見るというよりは、広く浅く見ていくことが重要かと思います。
DS検定を取得して、データサイエンティストやAI関連の仕事への道を開きましょう!
次回は「確率分布」などについて解説していきます。
ではまた~

DS検定の続きの解説は以下のページからどうぞ!


![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/214d380e.96fa3830.214d380f.9c4125c0/?me_id=1213310&item_id=20632239&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F8326%2F9784297128326_1_2.jpg%3F_ex%3D240x240&s=240x240&t=picttext)







コメント