データサイエンティスト検定対策｜データサイエンス力｜順列・確率・平均・分散を勉強

※本記事はアフィリエイト広告を含んでいます

[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]

最短突破　データサイエンティスト検定（リテラシーレベル）公式リファレンスブック　第2版 [ 菅由紀子 ]
価格：2,750円（税込、送料無料) (2023/5/18時点)

楽天で購入

どーも、りけーこっとんです。

DS検定の勉強をしよう！と思ったは良いものの、こんな悩みはありませんか？

とある女の子

DS検定ってどうやって勉強すればいいの？

DS検定の勉強の仕方が分からない…

とある男の子

本で勉強するのは分かるけど、高いなぁ…

無料で単語解説されているサイトとかないかな？

ひよっこDS

DS検定は、始まったばかりの試験だから、対策法とか分からないよね。

じゃあ、このサイトで出題範囲の内容を押さえていこう～

DS検定の解説をすぐ見たいよ！という方は、以下から最初の解説に飛べます。

ひよっこDS

今回はスキルチェックリスト

「DS１：順列や組み合わせの式を、適切に使い分けることができる」から

「DS４：分散・標準偏差・四分位などを理解し、使い分けられる」を解説していくよ～

本サイトでは超重要項目、重要項目、覚えておきたい項目と表記を分けますので、勉強時の参考にしてみてください。

DS検定って、そもそもどんな資格？という方は以下の記事をご覧くださいね。

試験範囲は以下の二つから出題されます。

・スキルチェックリスト
・数理、データサイエンス、AI（リテラシーレベル）モデルカリキュラム

本内容は以下の書籍を参考に作成しております。

楽天で購入

なお、本サイトはDS検定の合格を保証するわけではありませんので、ご了承ください。

では早速、内容に入っていきましょう！

※「DS○○：」項目の文章は独自に短縮して表現しております

DS１：順列や組み合わせの式を、適切に使い分けることができる
1. 順列
2. 組み合わせ
DS２：確率に関する基本的な概念の意味を説明できる
DS３：平均値・中央値・最頻値の算出方法の違いを説明できる
DS４：分散・標準偏差・四分位などを理解し、使い分けられる
まとめ

DS１：順列や組み合わせの式を、適切に使い分けることができる

順列や組み合わせって聞いたことありますかね？

高校一年生の数学で聞いたことある方も多いと思います。

この後、数字に「！」がついているものがあります。

「！」は「階乗」と呼ばれる計算で、数字を一つずつ減らしていき、全てを掛け算することで得られます。

（例） $$5! = 5\times4\times3\times2\times1 = 120$$

順列

順列（Permutation）：
複数の異なるものから、何個か選んで並べる場合の数。
（例）４枚のカードから３枚選んで１列に並べると、並べ方は何通りある？

式
$\displaystyle {}_n \mathrm{P}_k = \frac{n!}{(n-k)!}$

順列を具体例で計算すると、以下の通り。

$${}_4 \mathrm{P}_3 = \frac{4!}{(4-3)!} = \frac{4\times3\times\times2\times1}{1} = 24 通り$$

組み合わせ

組み合わせ（Combination）：
複数の異なるものから、何個か選ぶ組み合わせの数。
（例）４枚のカードから３枚選ぶと、その組み合わせの数は何通り？

式
$\displaystyle {}_n \mathrm{C}_k = \frac{n!}{k!(n-k)!}$

組み合わせを具体例で計算すると、以下のようになります。

$${}_4 \mathrm{C}_3 = \frac{4!}{3!(4-3)!} = \frac{4\times3\times\times2\times1}{(3\times2\times1)\times(1)} = 4 通り$$

「組み合わせは」異なるものから一定数選ぶ組み合わせの数、
さらに選んだものを並べるのが「順列」という意味になります。

この二つを使いこなせることが、DS１の要件ですね。

DS２：確率に関する基本的な概念の意味を説明できる

DS２の項目は、以下の４つを説明できますか？ということです。

・確率
・条件付き確率
・期待値
・独立

以上の４つを解説する前に、以下のキーワードも押さえておきましょう。

確率の基本概念を説明するための前提知識のようなものです。

試行：
複数の偶然で起こる結果があって、そのうち一つが偶然起こること。
（例）サイコロを振って1～6のいずれかの目が出ること

事象：
試行によって起きた結果のこと。
（例）サイコロを振って１が出る

確率変数：
確率で値が変わる数値のこと。
（例）サイコロの出目「1～6」、サイコロを３回振って１が出る「回数(1～3)」

では、メインの単語解説に行きましょう。

確率

確率とは？と聞かれると、以外と説明って難しいですよね。

先ほどの「事象」という言葉の意味を使うと、以下のように説明できます。

確率：「偶然起こる事象の起こりやすさ」のこと。

条件付き確率

条件付き確率は以下のように説明できます。

条件付き確率：
ある事象Bが起こる確率のもとで、事象Aが起こる確率のこと。
次のように表します。

$\displaystyle P(A|B) = \frac{P(A \cap B)}{P(B)}$

具体的な計算を見てみましょう。

Bの確率を「サイコロを振って偶数が出る確率」とします。
Aの確率を「サイコロで２が出る確率」としましょう。

すると$\displaystyle P(A|B)$の意味は
「サイコロを振って偶数が出たとき、その数が２である確率」となります。

Bの確率は$\displaystyle P(B) = \frac{3}{6}$でAの確率は$\displaystyle P(A) = \frac{1}{6}$ですね。

また「サイコロを振って偶数かつ、２である確率$\displaystyle P(A\cap B)$」は「２が出る確率」と同じです。

つまり$\displaystyle P(A\cap B) = \frac{1}{6}$ですね。

では、元の定義式に当てはめてみましょう。

$$P(A|B) = \frac{P(A\cap B)}{P(B)} = \frac{\frac{1}{6}}{\frac{3}{6}} = \frac{1}{3}$$

なので「サイコロを振って偶数が出たとき、その数が２である確率」は$\displaystyle \frac{1}{3}$です。

期待値

期待値も、よく聞く単語ではないでしょうか。

でも「説明して」と言われると難しいもの。

期待値：
確率変数にそれぞれ対応する確率をかけて、全て足した値。
次のように表します。$\displaystyle E(X)$

では、具体的にサイコロの出目で計算してみましょう。

（例）サイコロの出目の期待値 $$E(X) = 1\times\frac{1}{6} + 2\times\frac{1}{6} + 3\times\frac{1}{6} + 4\times\frac{1}{6} + 5\times\frac{1}{6} + 6\times\frac{1}{6} = 3.5$$

独立

「独立」は以下のように説明できます。

独立：
前に行った試行が次の試行に影響を与えないこと。試行について使う単語。
（例）同じコインを二回投げて、二回とも表の試行
⇒「この試行は独立」という

ちなみに、「独立」と似た言葉に「排反」というものがあります。

排反：
二つの事象が同時に起こらないこと。事象について使う単語。
（例）コインを一回投げて「表」と「裏」が同時に出る確率
⇒「表と裏の事象は互いに排反」という

DS３：平均値・中央値・最頻値の算出方法の違いを説明できる

DS３は、平均値・中央値・最頻値それぞれを説明できるかという項目。

それぞれ見ていきましょう。

平均値

平均値の説明ってできますかね？

りけーこっとんは「真ん中の値でしょ？」くらいに思ってました。

平均値：
全部のデータを足して、データの個数で割った値。
次のように表します。

$$\bar{X} = \frac{データの総和}{データの個数} = \frac{1}{n}\sum_{k=1}^{n}x_k$$

最後の式は難しそうに見えますが、それぞれのデータ$\displaystyle x$を1つ目から全部足した$\displaystyle \sum_{k=1}^{n}x_k$という操作になります。

数学的に正しく書くと、このような形になるんですね。

割と頻発する式なので、覚えておきましょう。

中央値

中央値と平均値、何が違うのでしょうか。

どちらも「真ん中の値」みたいなイメージがありますよね。

中央値：
データを小さい順に並べた時に、真ん中に来る値のこと。

※データの数が偶数個の時は、ちょうど真ん中に来る数字がありません。
そのため、中央に近い二つの値を足して２で割ります。

中央値は、単純に小さい順にデータを並べて「順番的に真ん中の値」という意味ですね。

平均値と中央値にズレがあると、「データに偏りがあるのかも…？」ということが予想できます。

最頻値

最頻値は以下のように定義されます。

最頻値：
データの中で一番多く出現した値のこと。

読んで字の通りで、「最」も「頻」繁に現れた「値」のことですね。

平均値・中央値・最頻値の具体的な計算

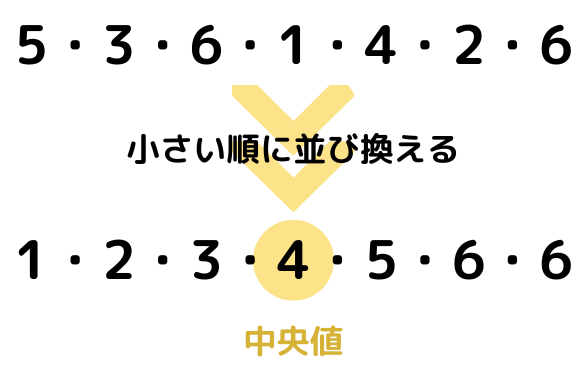
サイコロを振って「5・3・6・1・4・2・6」の順で数字が出たとします。
この時の「平均値」「中央値」「最頻値」を求めましょう。

平均値は以下のように計算できますね。

$$\bar{X} = \frac{データの総和}{データの個数} = \frac{5+3+6+1+4+2+6}{7} = 3.86$$

中央値は小さい順に並べた時に、真ん中に来る値です。

最頻値はデータの中で、最も多く出現した値のことでしたね。

今回は６が２回出ているので、最頻値は６です。

DS４：分散・標準偏差・四分位などを理解し、使い分けられる

DS４は、分散・標準偏差・四分位数・パーセンタイルそれぞれを説明できるかという項目。

一つ一つ解説していきますね。

分散

分散とは、以下のように定義されています。

分散：
データの散らばり具合を表す指標のこと。$\displaystyle \sigma^2$
「平均との差の二乗」を合計した平均の値。

平均値を$\displaystyle \bar{x}$とすると
$\displaystyle \sigma^2 = \frac{1}{n}\sum_{k=1}^{n}(x_k – \bar{x})^2$

分散が大きいほど、データのばらつきが大きいという意味になるんです。

しかし、分散は「単位が二乗になっている」という問題点があります。

例えば身長の場合、分散の単位は$\displaystyle cm^2$となってしまうんですね。

なので、数字が大きくなりすぎてしまうというのが問題です。

標準偏差

分散は「単位が二乗になっている」という問題点があるという説明をしました。

そこで、単位を元のデータと一緒にして、理解しやすくしたものが標準偏差です。

標準偏差：
分散にルートを取った値。$\displaystyle \sigma$

分散を$\displaystyle \sigma^2$とすると
$\displaystyle \sigma = \sqrt{\sigma^2}$

ルートを取ると＋－どちらも出てくるのでは？と思う人もいるでしょう。

基本的に標準偏差は、＋の値を使います。

データの散らばり具合を見たいからですね。

－の値は無視してかまいません。

四分位数

四分位数も、データの散らばりを見たい時に使う値です。

四分位数：
データを小さい順に並べた時に、４等分できる区切りの値。
区切りの値のため、基本的にはデータに３つ存在します。

小さい四分位数から順に
・第一四分位点（数）
・第二四分位点（数）
・第三四分位点（数）

※中央値と同じようにデータの数が偶数個の時は、ちょうど真ん中に来る数字がありません。
そのため、中央に近い二つの値を足して２で割ります。

先ほどと同じ例を使って四分位数を求めてみましょう。

サイコロを振って「5・3・6・1・4・2・6」の順で数字が出たとします。
この時の「第一四分位点」「第二四分位点」「第三四分位点」を求めましょう。

なので、
第一四分位点が2.5
第二四分位点が4
第三四分位点が5.5

という感じに求まりました。

パーセンタイル

パーセンタイルも、四分位数と同じようにデータの散らばりを見たい時に使う値です。

パーセンタイル：
データを小さい順に並べた時に、●●％に位置する値。

第一四分位点：25%パーセンタイル
第二四分位点：50%パーセンタイル
第三四分位点：75%パーセンタイル

四分位点に比べて、任意の位置でのデータの散らばり具合を見ることができます。

まとめ

今回は「順列・確率・平均・分散」などを解説してきました。

以下の項目を説明できるようになっているでしょうか？

・順列
・組み合わせ
・確率
・条件付き確率
・期待値
・独立
・平均値
・中央値
・最頻値
・分散
・標準偏差
・四分位数
・パーセンタイル

DS検定は覚える内容が多いです。

一つ一つを細部まで見るというよりは、広く浅く見ていくことが重要かと思います。

DS検定を取得して、データサイエンティストやAI関連の仕事への道を開きましょう！

次回は「母平均」「標準正規分布」「相関と因果」などについて解説していきます。

ではまた～

DS検定の続きの解説は以下のページからどうぞ！

DS検定対策｜データサイエンス力｜順列・確率・平均・分散を勉強