※本記事はアフィリエイト広告を含んでいます

どーも、りけーこっとんです。
「G検定取得してみたい!」「G検定の勉強始めた!」
このような、本格的にデータサイエンティストを目指そうとしている方はいないでしょうか?
また、こんな方はいませんか?
「なるべく費用をかけずにG検定取得したい」「G検定の内容について網羅的にまとまってるサイトが見たい」
今回はG検定の勉強をし始めた方、なるべく費用をかけたくない方にピッタリの内容。
りけーこっとんがG検定を勉強していく中で、新たに学んだ単語、内容をこの記事を通じてシェアしていこうと思います。
結構、文章量・知識量共に多くなっていくことが予想されます。
そこで、超重要項目と重要項目、覚えておきたい項目という形で表記の仕方を変えていきたいと思いますね。
早速G検定の中身について知りたいよ!という方は以下からどうぞ。

具体的にどうやって勉強したらいいの?
G検定ってどんな資格?
そんな方は以下の記事を参考にしてみてください。
なお、りけーこっとんは公式のシラバスを参考に勉強を進めています。
そこで主な勉強法としては
分からない単語出現 ⇒ web検索や参考書を通じて理解 ⇒ 暗記する
この流れです。
※この記事は合格を保証するものではありません
大項目「機械学習の具体的な手法」
G検定のシラバスを見てみると、試験内容が「大項目」「中項目」「学習項目」「詳細キーワード」と別れています。
本記事は「大項目」の「機械学習の具体的な手法」の内容。
その中でも「モデルの評価」というところに焦点を当ててキーワードを解説していきます。
G検定の大項目には以下の8つがあります。
・人工知能とは
・人工知能をめぐる動向
・人工知能分野の問題
・機械学習の具体的な手法
・ディープラーニングの概要
・ディープラーニングの手法
・ディープラーニングの社会実装に向けて
・数理統計
とくに太字にした「機械学習とディープラーニングの手法」が多めに出るようです。
本記事の範囲は、合格に向けては必須の基礎知識になります。
これから先の機械学習の理解を深めるために、そしてG検定合格するために、しっかり押さえておきましょう。
モデルの評価に関する内容が多くなってしまったので、記事を複数回に分割してお届けしようと思いますね。
モデルの評価というのは「作成したモデルが教師データや未知データに、どれだけ精度良く一致したか」を測るものになります。
つまり教師あり学習に用いられることが多い、というところは押さえておいてください。
精度評価指標はどこで使われるのか?
基本的には教師あり学習で用いられます。
教師あり学習の概要を以下に示しますね。
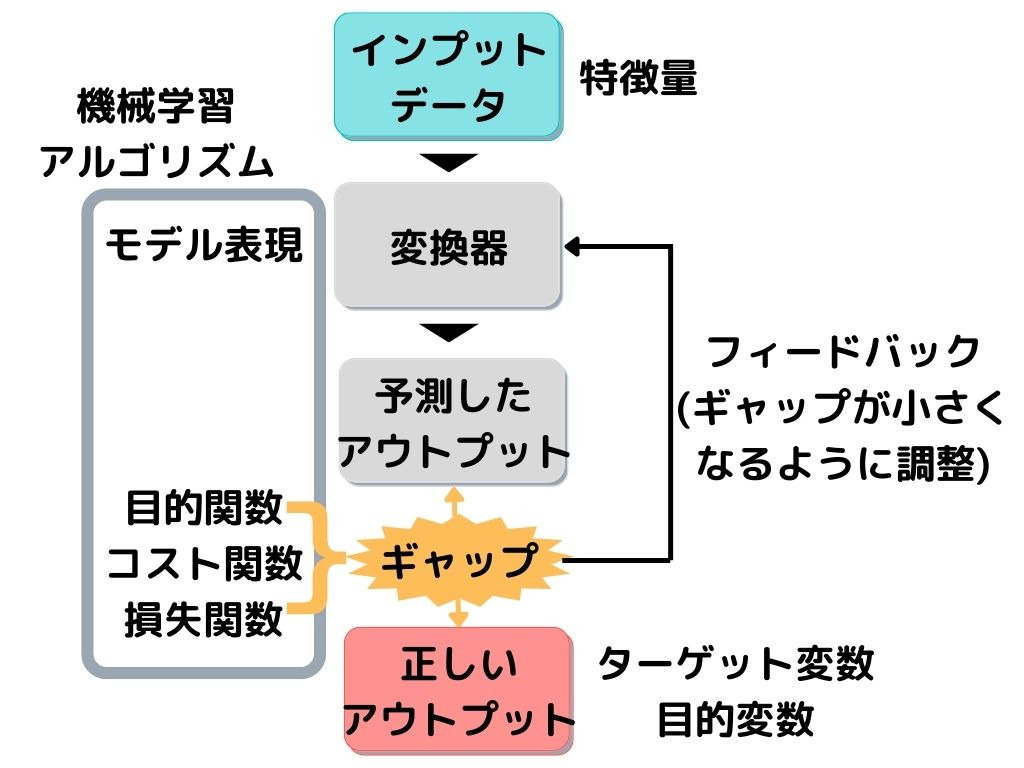
この図の「ギャップ」とある部分に、以下で紹介する精度評価指標が用いられます。
精度評価指標で出た「ギャップ(誤差)」が小さくなるように「変換器」を調整して、もう一回予測。
これを繰り返すことで、精度を高めて(ギャップを小さくして)いきます。
モデルの選択と情報量
前回触れた「分類問題・回帰問題の精度評価指標」は、基本的に教師あり学習の「誤差」に関する部分だけを見ていました。
「教師データ」に対して、たくさんの説明変数を使えば、誤差が小さくなることは予測できるのではないでしょうか。
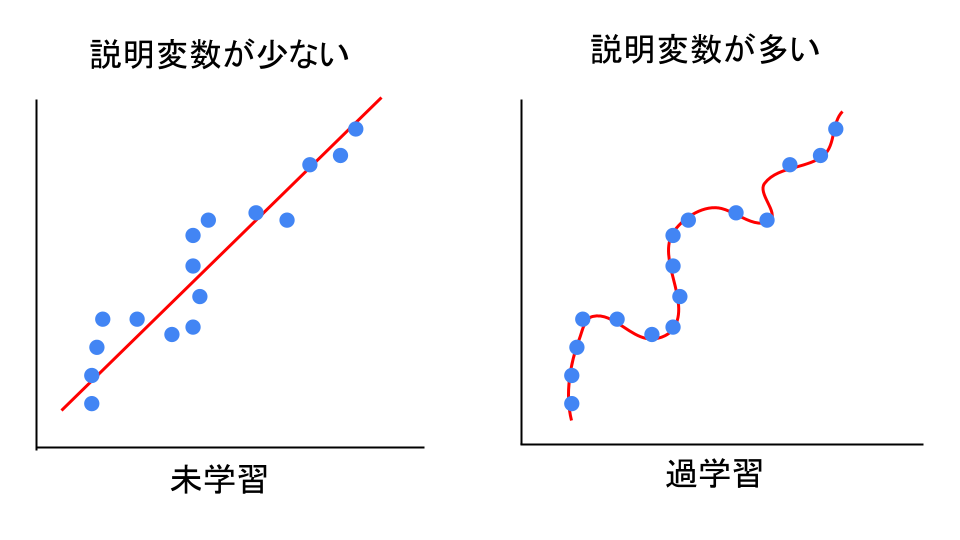
この図の右のように「教師データにモデルが一致しすぎている」状態を過学習、
逆に左のように「教師データにモデルが一致してなさ過ぎる」状態を未学習といいます。
しかし、あくまで「教師データ」との誤差です。
「教師データ」との誤差が小さくなりすぎると、今度は「未知データ」への予測精度が下がってしまいます。
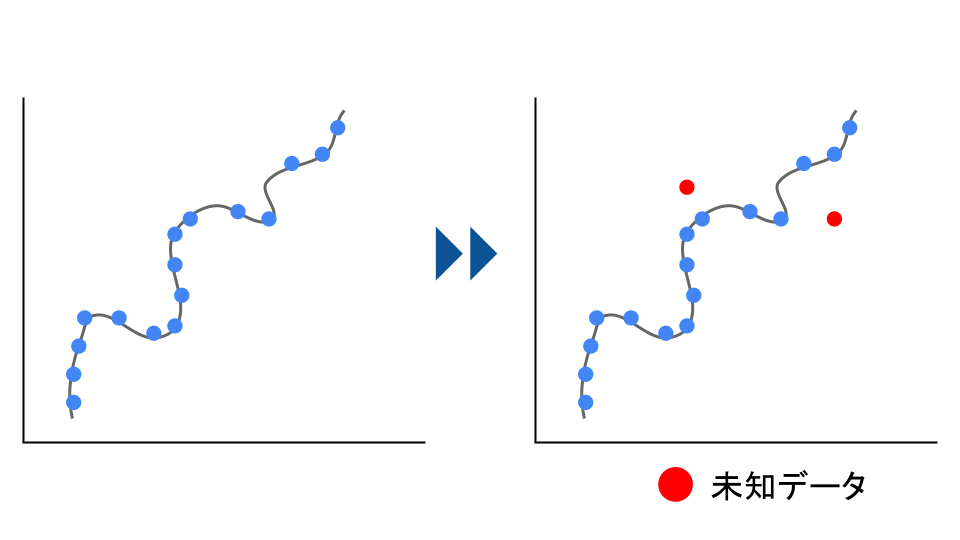
そこで統計学的な考え方に「オッカムの剃刀」という考え方があります。
オッカムの剃刀とは「ある事柄を説明するときには必要以上に多くを仮定するべきではない」という考え方のこと。
つまり、必要以上に説明変数を使わない方が良いよ、ということです。
前回触れた「分類問題・回帰問題の精度評価指標」は、誤差までしかわかりません。
しかし「ちょうど良い感じの説明変数の数でモデルをシンプルにして、でも予測精度も高い」ようにしたいですよね。
そこで「オッカムの剃刀」に従って、「なるべくシンプルな予測精度の高いモデル」を選択するための指標があります。
それが
・赤池情報量基準
・決定係数
・自由度調整済み決定係数
それぞれ見ていきましょう。

赤池情報量基準
赤池情報量基準(AIC)とは、「モデルの複雑さ」と「当てはまりの良さ」のバランスを取る指標のこと。
モデル選択のための基準の一つですね。
実際の式は以下の通り。

この式の「対数尤度」が当てはまりの良さ
「説明変数の数」がモデルの複雑さです。
この値は小さいほうが、良いモデルと言えます。
一つ気を付けたいのは、相対指標であるという事。
つまり「この値以下であればOK」というのではなく、
「前は40で、今は30で下がっているから、モデルは良くなっているね」と考えるという事です。
決定係数
決定係数とは、回帰モデルがどれだけ上手く教師データを説明できているかを測る指標。
モデル選択のための基準の一つです。
具体的な式は以下の通り。

横線しか引けない時の残差二乗和というのは以下のようなイメージ。
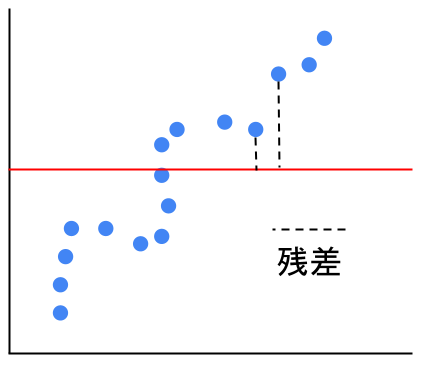
つまり「目的変数と説明変数に全く関係がない」と仮定したときの、残差二乗和です。
式まで覚える必要はないですが「統計検定三級程度の知識」は出るようなので、イメージできた方が良いかもしれませんね。(統計検定の範囲は良く分からないです)
以下のことは覚えておいてもいいでしょう。
・残差二乗和の比率は小さい方が良いので、式全体としては1に近い方が「当てはまりがいいモデル」
・実際には説明変数がたくさんある事が多いので、モデル同士の当てはまりの良さの比較には使えない
自由度調整済み決定係数
自由度調整済み決定係数とは、説明変数の数が多いときに使う決定係数。
モデル選択のための基準の一つですね。
こちらも決定係数と同様、1に近い方が良いという事になっています。
具体的な式は以下の通り。

こちらも式が複雑なので、覚える必要はありません。
しかし、「機械学習において、決定係数よりも使われる指標」という事は覚えましょう。
第一種の過誤・第二種の過誤
第一種の過誤・第二種の過誤とは、以下の図のようなイメージ。
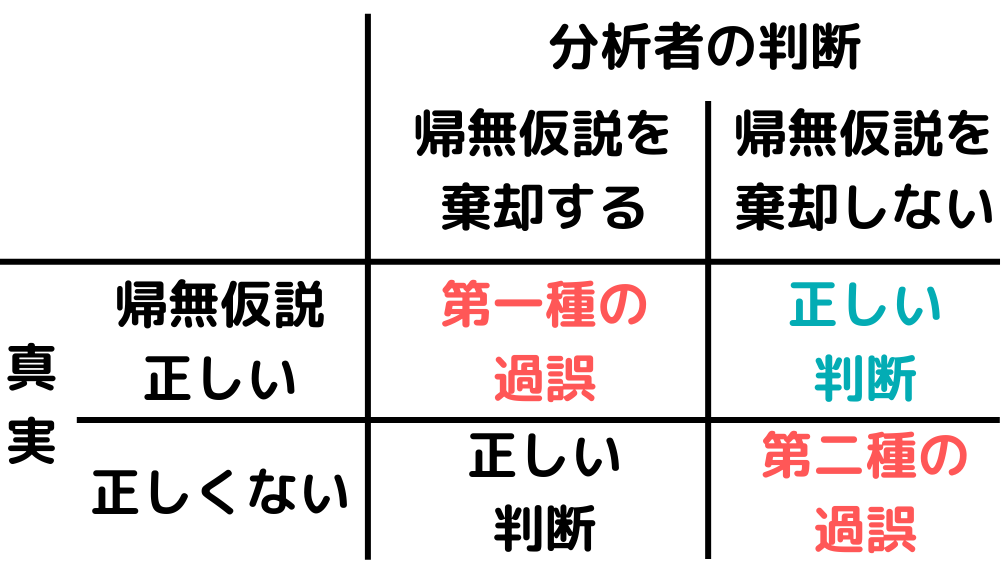
これを理解するには、帰無仮説という統計学の知識を知っていないといけません。
簡単に言うと帰無仮説とは「この仮説は違うって言いたい(無に帰したい)仮説」のことです。
例えば「身長が大きくなると、体重も増える」というグラフがあったとしましょう。
この真実を証明するために「身長と体重には全く関係がない」という仮説を立てます。
「関係がない」仮説を、違うと否定することで「やっぱり元の”身長が大きくなると、体重も増える”は正しかったね」と言えますね。
この時「身長と体重には全く関係がない」という仮説を帰無仮説と言います。
回りくどい方法ですが、帰無仮説が間違っていないかどうかを考える時に出てくるのが「第一種の過誤・第二種の過誤」という考え方ですね。
まとめ
今回は大項目「機械学習の具体的な手法」の中の一つモデルの評価についての解説、第二弾でした。
本記事の重要キーワードは以下。
・過学習
・未学習
・オッカムの剃刀
・赤池情報量基準(AIC)
・第一種の過誤・第二種の過誤
以上が大項目「機械学習の具体的な手法」の中の一つモデルの評価の内容でした。
今回は、統計学的な考え方のモデルの評価に焦点を当てていました。
次回は「モデルの評価」最終回!
覚える内容が多いですが、りけーこっとんも頑張ります!
ではまた~

続きは以下のページからどうぞ!










コメント