※本記事はアフィリエイト広告を含んでいます

どーも、りけーこっとんです。
「G検定取得してみたい!」「G検定の勉強始めた!」
このような、本格的にデータサイエンティストを目指そうとしている方はいないでしょうか?
また、こんな方はいませんか?
「なるべく費用をかけずにG検定取得したい」「G検定の内容について網羅的にまとまってるサイトが見たい」
今回はG検定の勉強をし始めた方、なるべく費用をかけたくない方にピッタリの内容。
りけーこっとんがG検定を勉強していく中で、新たに学んだ単語、内容をこの記事を通じてシェアしていこうと思います。
結構、文章量・知識量共に多くなっていくことが予想されます。
そこで、超重要項目と重要項目、覚えておきたい項目という形で表記の仕方を変えていきたいと思いますね。
早速G検定の中身について知りたいよ!という方は以下からどうぞ。

具体的にどうやって勉強したらいいの?
G検定ってどんな資格?
そんな方は以下の記事を参考にしてみてください。
なお、りけーこっとんは公式のシラバスを参考に勉強を進めています。
そこで主な勉強法としては
分からない単語出現 ⇒ web検索や参考書を通じて理解 ⇒ 暗記する
この流れです。
※この記事は合格を保証するものではありません
大項目「機械学習の具体的な手法」
G検定のシラバスを見てみると、試験内容が「大項目」「中項目」「学習項目」「詳細キーワード」と別れています。
本記事は「大項目」の「機械学習の具体的な手法」の内容。
その中でも「教師あり学習」というところに焦点を当ててキーワードを解説していきます。
G検定の大項目には以下の8つがあります。
・人工知能とは
・人工知能をめぐる動向
・人工知能分野の問題
・機械学習の具体的な手法
・ディープラーニングの概要
・ディープラーニングの手法
・ディープラーニングの社会実装に向けて
・数理統計
とくに太字にした「機械学習とディープラーニングの手法」が多めに出るようです。
本記事の範囲は、合格に向けては必須の基礎知識になります。
これから先の機械学習の理解を深めるために、そしてG検定合格するために、しっかり押さえておきましょう。
教師あり学習に関する内容が多くなってしまったので、記事を複数回に分割してお届けしようと思いますね。
教師あり学習の概要
教師あり学習とは教師データ(正解データ)に、学習の結果を近づけようとする機械学習の手法。
教師データ(正解データ)とは予め人間が用意したデータで、データの通りに機械が予測できれば正解、そうでなければ不正解となるデータのことです。
例えば犬と猫の画像があったとしましょう。
人間が用意した犬と猫の画像は「教師データ」です。
機械が画像に何が写っているかを予測した結果、犬を犬、猫を猫と出せるようにしたいのが、教師あり学習。
全体的な構成は以下の画像の通り。
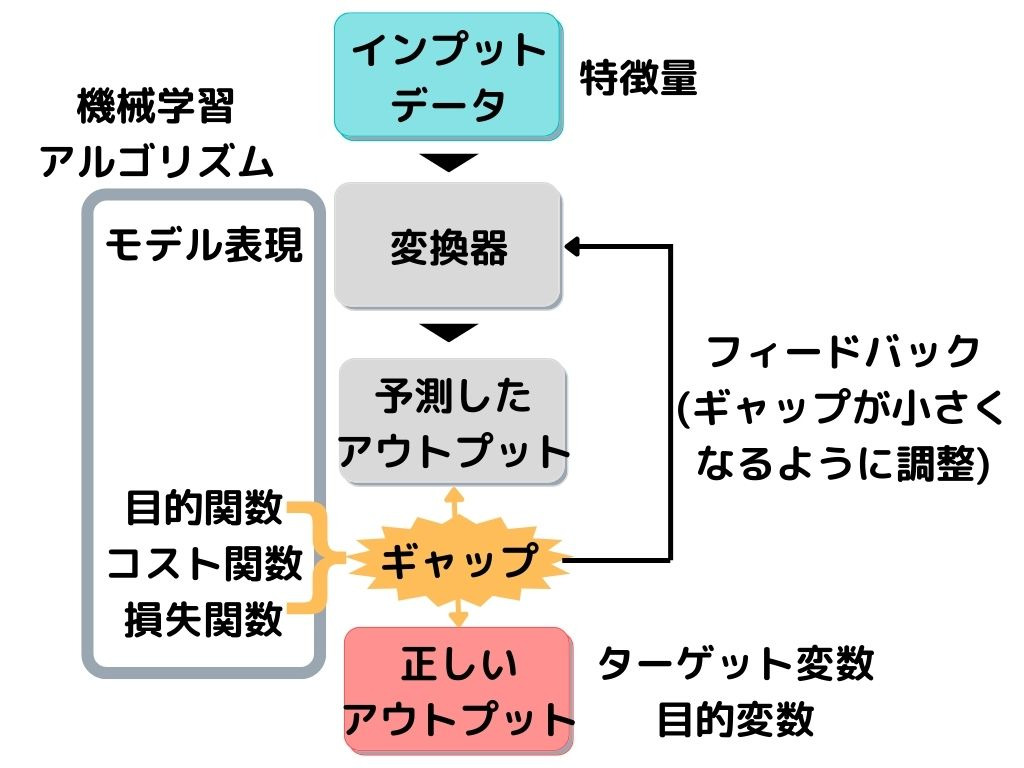
教師データは上の図で言うと「正しいアウトプット」に相当します。
専門用語だと「ターゲット変数」「目的変数」なんて言ったりもしますね。
変換器が「予測したアウトプット」と「正しいアウトプット」のギャップ(誤差)を埋めるために、何回も調整(学習)するのが、教師あり学習です。
これから出てくる手法は全て「変換器」の部分。
専門用語では変換器を「モデル表現」、ギャップや誤差を「目的関数・コスト関数・損失関数」なんても言います。
このモデル表現や目的関数を合わせて「機械学習アルゴリズム」と言ったりもしますね。
そして変換器に入力するデータが「特徴量」と言われます。
りけーこっとんは、よく目的関数と目的変数がごっちゃになります。
これから示す方法は全て、「変換器・モデル表現」の中の話です。
では、一つずつ見ていきましょう。
最近傍法
最近傍法とは入力パターンと学習パターンの距離を計算し、最も近いデータのカテゴリを入力パターン分類として出力すること。
モデル表現の一つですね。
この方法の手順は次の通り。
1.既にある「教師データ」がグラフにプロットされています。
2.次に未知データが入力され、新しい点がグラフにプロットされますよね。
3.その「未知データの新しい点」と「教師データの点」の最も近い距離を計算します。
4.そこで最も近い教師データを「未知のデータも同じ結果になるだろう」と予想して出力する。
今までのデータと照らし合わせて、条件が一番近いものに未知データもなるでしょう
という考えで行っている、最も簡単な方法です。
k近傍法
k近傍法とは入力パターンに近いk個の学習パターンを取り上げて、最多のカテゴリを入力パターン分類として出力すること。
方法としては、最近傍法(直前の章)とほぼ一緒です。
違うのは、3と4。
3で距離を計算するときに、最も近い点だけではなく、近い順にk個の点からの距離を計算します。
4はk個の中で最も多い教師データの結果を「未知のデータも同じ結果になるだろう」と予想して出力する。
この方法は、最近傍法に比べて、外れ値に強い特徴を持っています。
1点しか取らないと、その1点が外れ値だった場合に、間違った分類をしてしまいますよね。

サポートベクターマシン(SVM)
サポートベクターマシン(SVM)とは、マージンを最大化するような境界線を決定すること。
マージンについては、後述しますね。
ここで大事なのは「境界線」という線を引くこと。
先ほどまでの近傍法とは違って、明確な線が引かれます。
境界線を明確にできそう、させたいというときに使えそうです。
マージン
マージンとは境界線と最も近い、データとの距離(ベクトル)のこと。
図で示すとこんな感じ。
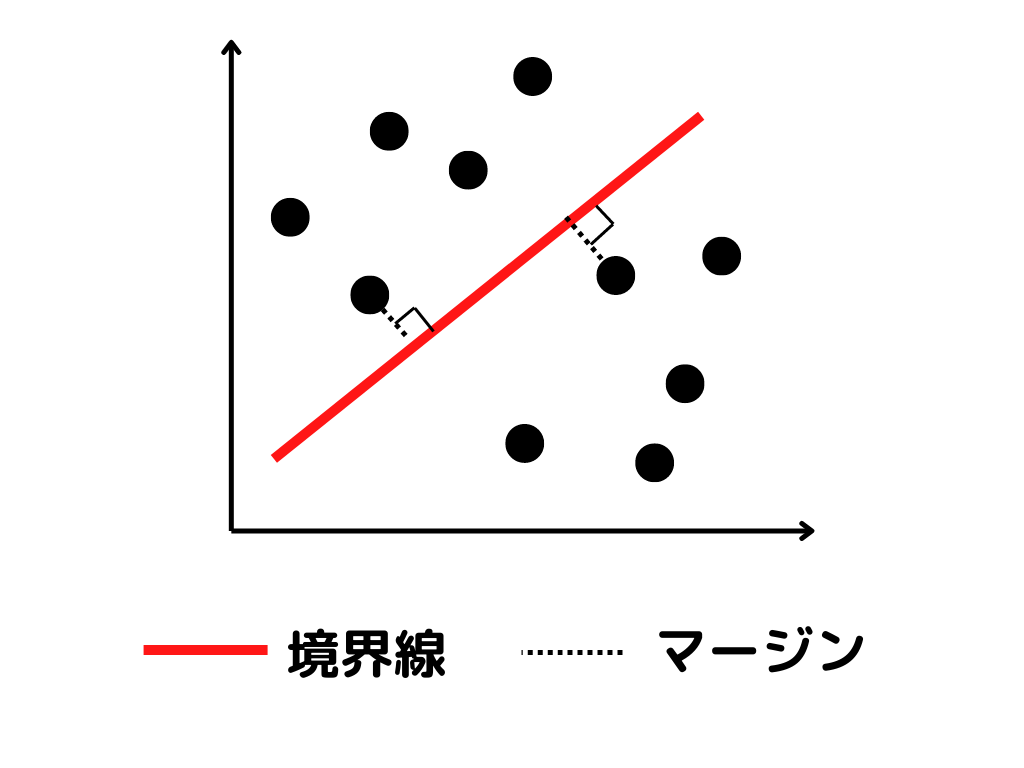
言葉で説明すると、
境界線に最も近いデータから、境界線に下ろした垂線の長さ
となります。
この長さが最も長くなるように、境界線を引いていくのがサポートベクターマシンです。
ハードマージン
ハードマージンとはデータがA,Bできっぱり分けられることを前提とした、境界線の引き方のこと。
計算は、先ほどまで述べてきた方法で行います。
ただし、そう上手くはいかないのが現実世界。
そこで外れ値にも対応できるようにした引き方が、次のソフトマージンです。
ソフトマージン
ソフトマージンとはデータがA,Bできっぱり分けられないことを考慮した、境界線の引き方のこと。
現実世界では、A,Bできっぱり分けられないデータというものが多いですよね。
何個かは、違うデータの分類に入ってしまうことがあります。
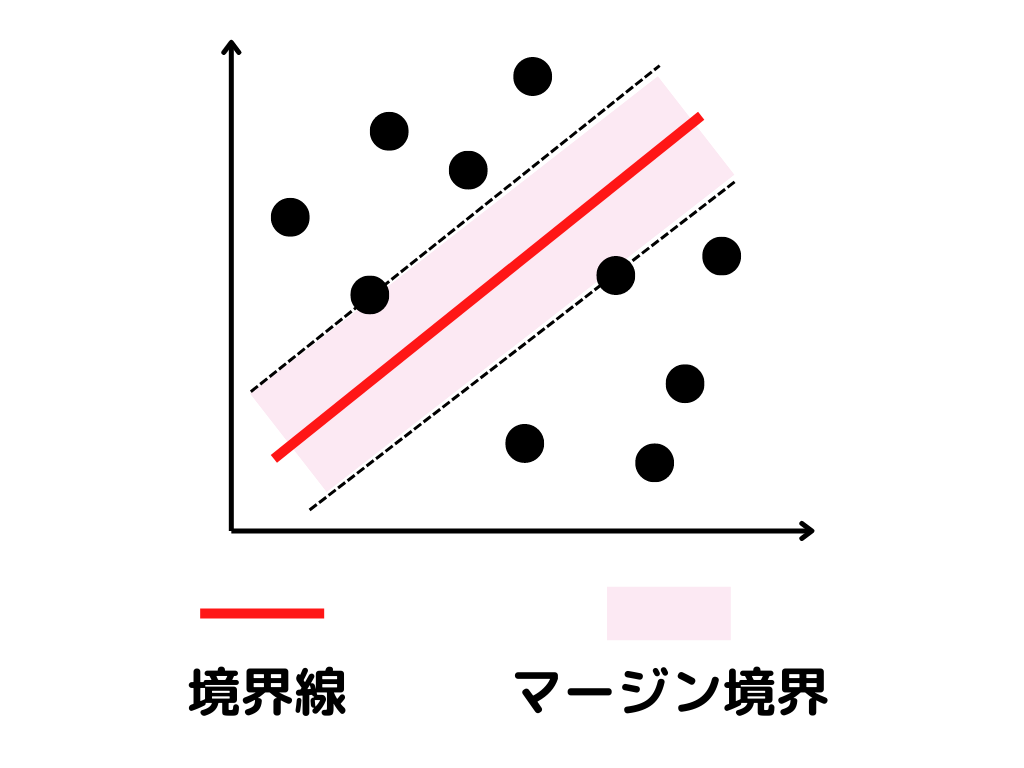
そこで”誤分類したデータ”と、”マージン境界内に入ったデータ”に対してペナルティを与えます。
こうすることで、何個かは違う分類のデータがあったとしても、”違うデータが入っていることを考慮した”線の引き方ができるんです。
マージン境界内というのは、図で言うと点線の内側の部分。
カーネル関数
カーネル関数とは直線では分類できない複雑なデータを、高次元(2⇒3次元)に写像するための関数のこと。
ここまでの話を聞いて、「直線だけじゃ分類できない問題もあるでしょ」と思ったあなた。
その通りです。
そこで、曲線だったり円形だったりしても、分類できるようにする関数がカーネル関数です。
詳しい話はG検定の対策からは外れそうなのと、りけーこっとんがまだ理解していないというのがあるので、「こういう関数があるんだ」という理解で十分だと思います。
カーネルトリック
カーネルトリックとはカーネル関数を使って写像したデータで分類して、元の次元に戻すことで分類できる手法のこと。
カーネルトリックを使った分類の手順としてはこんな感じ。
1.カーネル関数を使って、データを高次元に写像する(G検定対策には、詳しいところまで知らなくても、手順が分かっていれば十分かと)
2.高次元の空間で境界線を引く
3.データと境界線を、元の次元に戻すことで、複雑な線が引けている
イメージも難しいので「こういうものがあるんだ」位に留めておきましょう。
ラッソ(Lasso)回帰
ラッソ(Lasso)回帰とは以下の式を最小化するように学習する手法のこと。
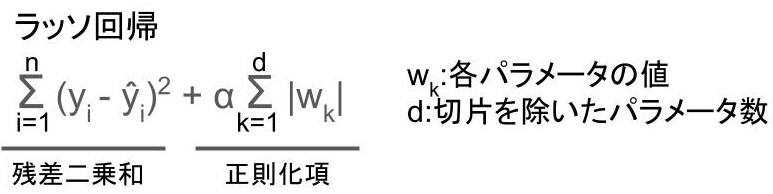
残差二乗和、覚えているでしょうか?
正則化項というのは、過学習を防ぐための部分です。
wのパラメータというのは、単純なものだと「切片」と「傾き」のことですね。
αはパラメータの大きさを、どれだけ制限したいかによって、分析者自身が決めます。
これはハイパーパラメータといっていましたね。
ラッソ回帰のように、パラメータの絶対値の和を用いた正則化のことを、L1正則化と言うようです。
使いどころとしては特徴量の数が膨大で、ほとんどの要素が0の場合などに使えますね。
こういう場合は自然言語処理分野などに見られるそうです。
リッジ(Ridge)回帰
リッジ(Ridge)回帰とは以下の式を最小化するように学習する手法のこと。
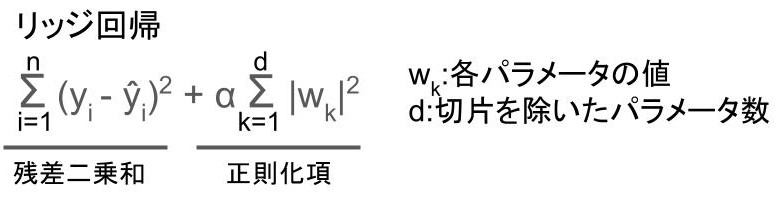
ラッソ回帰とほぼ同じですね。
異なる点は、正則化項が絶対値の二乗になっている点。
それ以外はラッソ回帰と一緒です。
リッジ回帰のように、パラメータの絶対値の二乗和を用いた正則化のことを、L2正則化と言うようです。
使いどころとしては特徴量が多く、多重共線性による問題や過学習が起こる恐れのある場合。
多重共線性とは、ある特徴量が別の特徴量で説明できてしまうことで、発生すると学習が上手く進まなくなってしまいます。
例えば以下の様な式があったとしましょう。

このように、ある変数を別の変数で説明できてしまうことを、多重共線性といいます。
自己回帰モデル
自己回帰モデルとは1変数のある時刻tの値を、時刻tよりも古いデータを使って予測・説明すること。
自然科学や経済学など、時間に対して変動する過程を知りたいときなどに使うようです。
さらに自己回帰モデルを拡張したものとしてベクトル自己回帰モデルもあります。
ベクトル自己回帰モデルとは、2変数以上を時刻tより古いデータを使って予測・説明すること。
1変数のみだった「自己回帰モデル」に対して、2変数以上に適用することで、拡張していると言えますね。
まとめ
今回は大項目「機械学習の具体的手法」の中の一つ教師あり学習についての解説、第二弾でした。
本記事の覚えておきたいキーワードは以下。
・最近傍法
・k近傍法
・サポートベクターマシン(SVM)
・ラッソ(Lasso)回帰
・リッジ(Ridge)回帰
・自己回帰モデル
以上が大項目「機械学習の具体的手法」の中の一つ教師あり学習の内容でした。
実は教師あり学習は、まだ他にも手法があります。
そこで、次回は「機械学習の具体的手法」の中の一つ教師あり学習の第三弾!
思ったより記事が長くなってしまってすみません。
それだけ押さえておきたいところが多いということ。
覚える内容が多いですが、りけーこっとんも頑張ります!一緒に頑張っていきましょう!
ではまた~

続きは以下のページからどうぞ!










コメント