DS検定対策|データサイエンス力|推定・検定・帰無仮説などを勉強!

※本記事はアフィリエイト広告を含んでいます

どーも、りけーこっとんです。
DS検定の勉強をしよう!と思ったは良いものの、こんな悩みはありませんか?
DS検定の勉強の仕方が分からない…
無料で単語解説されているサイトとかないかな?
じゃあ、このサイトで出題範囲の内容を押さえていこう~
DS検定の解説をすぐ見たいよ!という方は、以下から最初の解説に飛べます。

「DS76:点推定と区間推定の違いを説明できる」から
「DS78:第一種の過誤・第二種の過誤・p値・有意水準を説明できる」を解説していくよ~
本サイトでは超重要項目、重要項目、覚えておきたい項目と表記を分けますので、勉強時の参考にしてみてください。
DS検定って、そもそもどんな資格?という方はこちらの記事をご覧くださいね。
試験範囲は以下の二つから出題されます。
・スキルチェックリスト
・数理、データサイエンス、AI(リテラシーレベル)モデルカリキュラム
本内容は以下の書籍を参考に作成しております。
|
|
なお、本サイトはDS検定の合格を保証するわけではありませんので、ご了承ください。
では早速、内容に入っていきましょう!
※「DS○○:」項目の文章は独自に短縮して表現しております
目次
DS76:点推定と区間推定の違いを説明できる
「点推定」も「区間推定」も推測統計学の専門用語です。
統計学といっても2種類あって、「記述統計学」と「推測統計学」に分かれることを知っていたでしょうか。
「記述統計学」はデータの平均・分散を計算したり、グラフを書いたりしてデータの性質を読み解くためのもの。
「推測統計学」はランダムに集めたデータから、母集団の特徴を抽出するためのものです。
テレビの視聴率調査などが近い例でしょうか。
集めたデータから、母集団の特徴を「推測」するための方法として「点推定」や「区間推定」があります。
点推定
点推定
平均値、分散などを一つの値(点)で推測する方法。
例)
標本の平均が3.5だった ⇒ 母集団の平均も3.5だろう
「点推定」とは、文字通り「1点」の値で推測する手法ですね。
平均値の場合は「標本平均=母平均」とすることも多く、手軽に計算できます。
しかし、1点で推測すると「本当にその1点ピンポイントで当たってるの?」という不安が出てきますよね。
そこで「区間推定」を用います。
区間推定
区間推定
「信頼区間」と呼ばれる幅を用いて、平均値・分散などを推測する手法。
信頼区間が狭い、ということは推定の精度が高いという意味。
例)
A. 99%の信頼区間が3.4 ~ 3.6 ⇒ 推定の精度が高い
B. 99%の信頼区間が0 ~ 10 ⇒ 推定の精度が低い
幅で推定するので、点推定よりも直感的ではないでしょうか。
「99%の信頼区間が3.4 ~ 3.6」というのは、値が3.4から3.6に収まる確率が99%という意味になります。(厳密には少し違うのですが、DS検定においてはこの理解で問題ないでしょう)
DS77:帰無仮説と対立仮説の違いを説明できる
推測統計学の中には、前章で出てきた「推定」と似た言葉に「検定」というものが存在します。
混同しやすいので、区別して覚えましょう。
「検定」とは、母集団の特徴について立てた仮説が正しいかどうかを判断すること。
検定のやり方・考え方が少々特殊ですので、しっかり理解したいところです。
まず検定を解説するに当たって、「帰無仮説」「対立仮説」について理解しましょう。
帰無仮説
帰無仮説
推測統計学の検定において、否定したい仮説のこと。
例)
新薬と、既存の薬で風邪が治る確率が変わらない
コインの表が出る確率が\(\displaystyle \frac{1}{5}\)である
車と猫は同じ
検定では最初に、帰無仮説を立てます。
否定したい仮説から立てるわけですね。
間違って、本当だと証明したい仮説を帰無仮説にしないようにしましょう。
つまり、例に挙げているように「否定したい」仮説を立てているわけです。
対立仮説
対立仮説
推測統計学の検定において、本当だと証明したい仮説のこと。帰無仮説を否定する仮説を立てる。
例)
新薬と、既存の薬で風邪が治る確率に差がある
コインの表が出る確率が\(\displaystyle \frac{1}{5}\)ではない
車と猫は同じではない
帰無仮説を立てたら、対立仮説を立てます。
対立仮説は帰無仮説の否定形を作ることが重要。
ここで「コインの表が出る確率が\(\displaystyle \frac{1}{2}\)である」みたいな仮説は立ててはいけないわけです。
「検定」においては、帰無仮説を否定するまでがゴールなので「コインの表が出る確率が\(\displaystyle \frac{1}{5}\)ではない」としか言えません。
つまり、このような仮説を立てた場合には表が出る確率は\(\displaystyle \frac{1}{2}\)かもしれないし\(\displaystyle \frac{1}{10}\)かもしれないということです。
検定
帰無仮説、対立仮説ついて分かったところで、検定の手順について解説します。
検定の手順
1.帰無仮説を立てる
2.対立仮説を立てる
3.帰無仮説を否定する(棄却する)
1.まずは帰無仮説を立てます。
ここでは、否定したい仮説を立てることが重要でしたね。
2.次に対立仮説を立てます。
あくまでも帰無仮説の否定しかできないことに注意が必要でした。
3.最後に帰無仮説が起こる確率を調べます。
帰無仮説が起こる確率が大きいと、帰無仮説が起こりにくいとは言いにくいですよね。
つまり帰無仮説が否定(棄却)できず、対立仮説が正しいとは言えません。
帰無仮説が起こる確率が小さいと、帰無仮説が起こりにくいと言えます。
つまり帰無仮説が否定(棄却)でき、対立仮説が正しいと言えることになります。

DS78:第一種の過誤・第二種の過誤・p値・有意水準を説明できる
この項目の用語は全て、推測統計学の「検定」に出てくる単語です。
それぞれ詳しく見ていきましょう。
第一種の過誤・第二種の過誤
第一種の過誤・第二種の過誤
検定の際に、間違った判断をした場合を表した単語。
以下の図のような分類に分けられる。
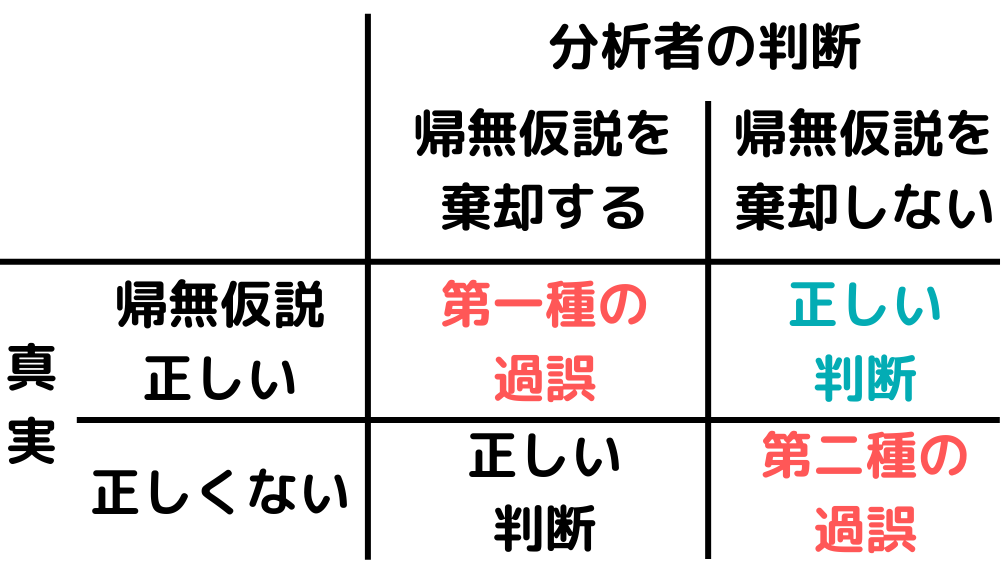
検定の正誤を判断するには「帰無仮説が正しいか否か」と「帰無仮説を棄却するか否か」で決まります。
帰無仮説が正しいという真実だった場合、帰無仮説を棄却してはいけません。
つまり帰無仮説が正しいのに、帰無仮説を棄却してしまうことを「第一種の過誤」といいます。
逆に帰無仮説が正しくないという真実だった場合、帰無仮説を棄却するべきですよね。
つまり帰無仮説が正しくないのに、帰無仮説を棄却できないことを「第二種の過誤」といいます。
有意水準
有意水準
滅多に起こらないと判断する基準のこと。帰無仮説を棄却するときに、基準となる確率のこと。
有意水準は、分析者自身で決めることになります。
どれくらいの確率以下であれば、滅多に起こらないと判断していいのかを決めなければなりません。
よく使われる有意水準は5%や1%という数値です。
しかし、何も考えずにこの数字を使っておけばいいということではないことに注意しましょう。
p値
p値
帰無仮説を正しいとした場合に、観測した事象よりも極端な事象が起こる確率のこと。
・事前に定めた有意水準を上回れば「よく起こること」
・事前に定めた有意水準を下回れば「めったに起こらないこと」
と判断できる
p値は、前の章で説明した「有意水準」と比べるための確率になります。
有意水準は「帰無仮説を棄却するときに判断となる基準」でした。
p値が有意水準を下回れば帰無仮説が棄却できます。
しかしp値は、帰無仮説が棄却できるかどうかを判断するための指標にすぎません。
「p値が小さいほどコインの表が出る確率が\(\displaystyle \frac{1}{2}\)である」「p値が大きいほど薬が効きにくい」という判断はできないので、注意しましょう。
まとめ
今回は「推定・検定」などを解説してきました。
以下の項目を説明できるようになっているでしょうか?
・点推定
・区間推定
・検定
・帰無仮説
・対立仮説
・第一種の過誤、第二種の過誤
・有意水準
・p値
DS検定は覚える内容が多いです。
一つ一つを細部まで見るというよりは、広く浅く見ていくことが重要かと思います。
DS検定を取得して、データサイエンティストやAI関連の仕事への道を開きましょう!
次回は「片側検定・両側検定」「t検定」「z検定」などについて解説していきます。
ではまた~

DS検定の続きの解説は以下のページからどうぞ!

![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/214d380e.96fa3830.214d380f.9c4125c0/?me_id=1213310&item_id=20632239&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F8326%2F9784297128326_1_2.jpg%3F_ex%3D240x240&s=240x240&t=picttext)











