※本記事はアフィリエイト広告を含んでいます
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/214d380e.96fa3830.214d380f.9c4125c0/?me_id=1213310&item_id=20632239&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F8326%2F9784297128326_1_2.jpg%3F_ex%3D240x240&s=240x240&t=picttext "[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]")
どーも、りけーこっとんです。
DS検定の勉強をしよう！と思ったは良いものの、こんな悩みはありませんか？
DS検定ってどうやって勉強すればいいの？
DS検定の勉強の仕方が分からない…
本で勉強するのは分かるけど、高いなぁ…
無料で単語解説されているサイトとかないかな？
DS検定は、始まったばかりの試験だから、対策法とか分からないよね。
じゃあ、このサイトで出題範囲の内容を押さえていこう～
DS検定の解説をすぐ見たいよ！という方は、以下から最初の解説に飛べます。
今回はスキルチェックリスト
「DS９５：ヒストグラムを作成し、バラツキを把握できる」から
「DS１１２：因果効果を推定したい場合、交絡因子の考慮が重要」を解説していくよ～
本サイトでは超重要項目、重要項目、覚えておきたい項目と表記を分けますので、勉強時の参考にしてみてください。
DS検定って、そもそもどんな資格？という方は以下の記事をご覧くださいね。
試験範囲は以下の二つから出題されます。
・スキルチェックリスト
・数理、データサイエンス、AI（リテラシーレベル）モデルカリキュラム
本内容は以下の書籍を参考に作成しております。
なお、本サイトはDS検定の合格を保証するわけではありませんので、ご了承ください。
では早速、内容に入っていきましょう！
※「DS○○：」項目の文章は独自に短縮して表現しております
DS９５：ヒストグラムを作成し、バラツキを把握できる
この項目はヒストグラムを描いて、バラツキも理解できる、という項目です。
しかしヒストグラムを描こうにも、そもそもどういうものかを知らなければ書けません。
ヒストグラムとは何か？というところから見ていきましょう。
ヒストグラム
ヒストグラム
データを一定の範囲ごとに区切って、範囲内にあるデータの数を数えたグラフのこと。
以下の図のようなイメージ。
図の縦軸は「度数」とも言われ、一定の範囲に収まるデータの数を示す。
では、以下のデータを例に取って、ヒストグラムを作成しましょう。
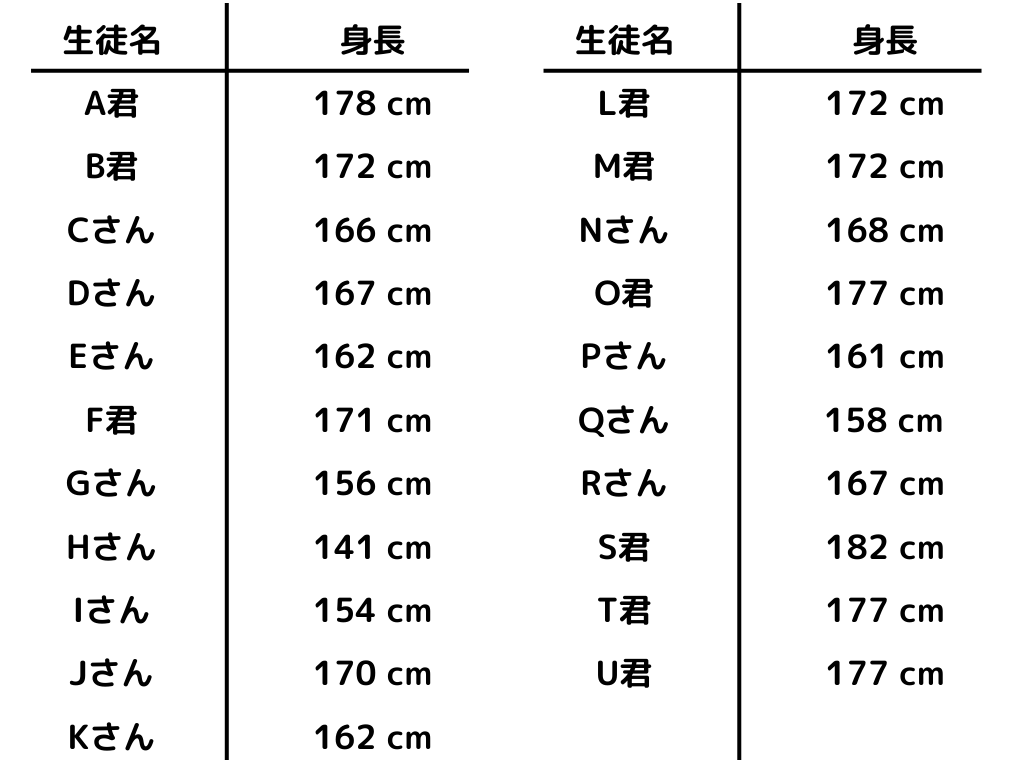
１．一定の範囲（階級）を定める。
まずはデータを区切る範囲を定めます。
適切な階級の幅を定めないと、データの分布が適切に把握できません。
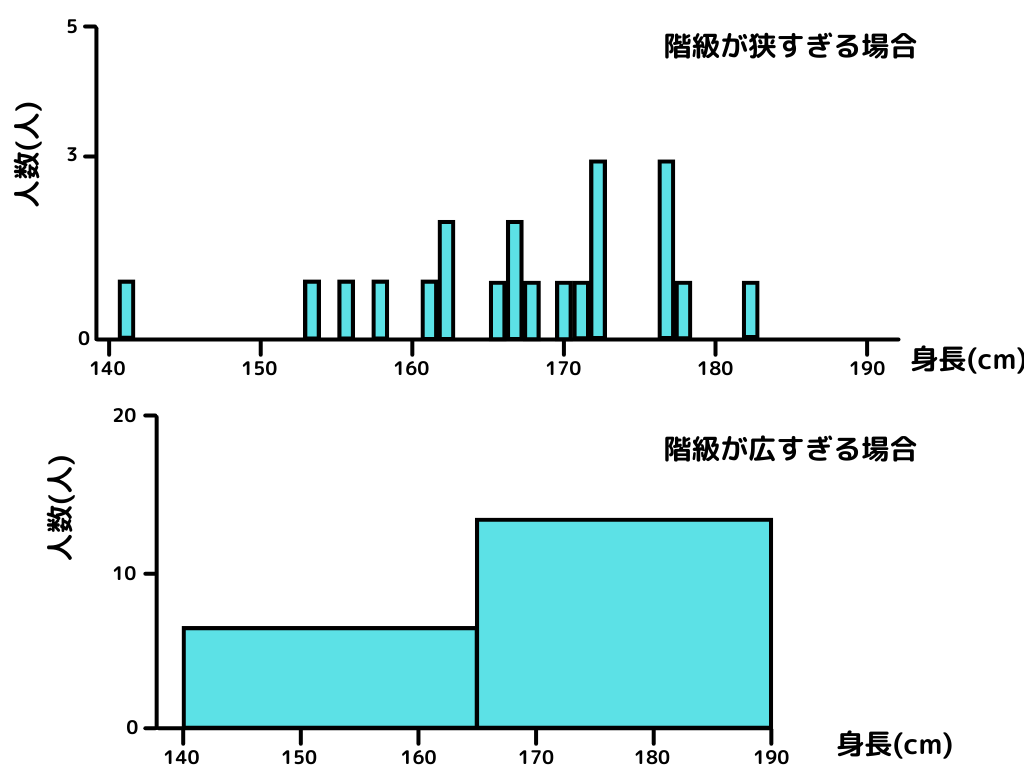
データの最大値・最小値を見るなどして、適切な階級の幅を考えましょう。
今回は5 cmずつで区切ります。
２．階級に収まるデータの数（度数）を数える。
区切った階級の幅に収まるデータ数（今回は人数）を数えます。
140 cm以上145 cm未満は1人、145 cm以上150 cm未満は0人、といった感じですね。
３．横軸に階級・縦軸に度数を取って、棒グラフを描く
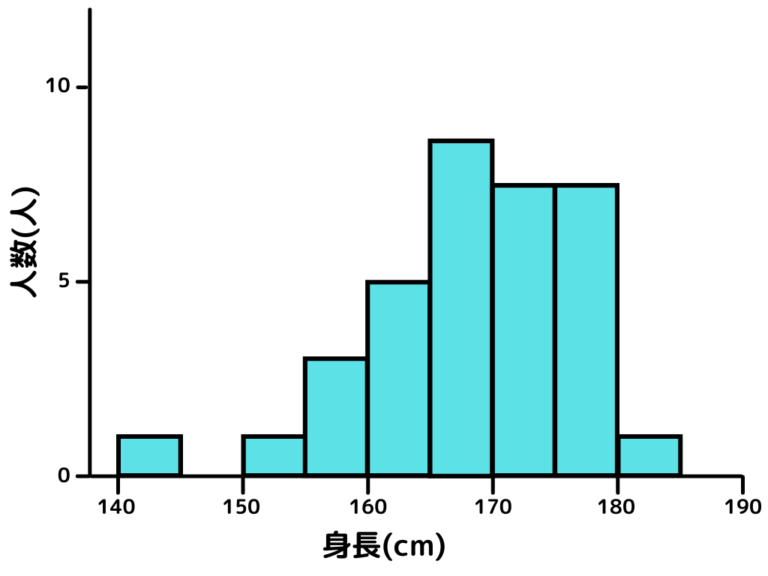
適切な階級幅でヒストグラムを描くと以下の通り。
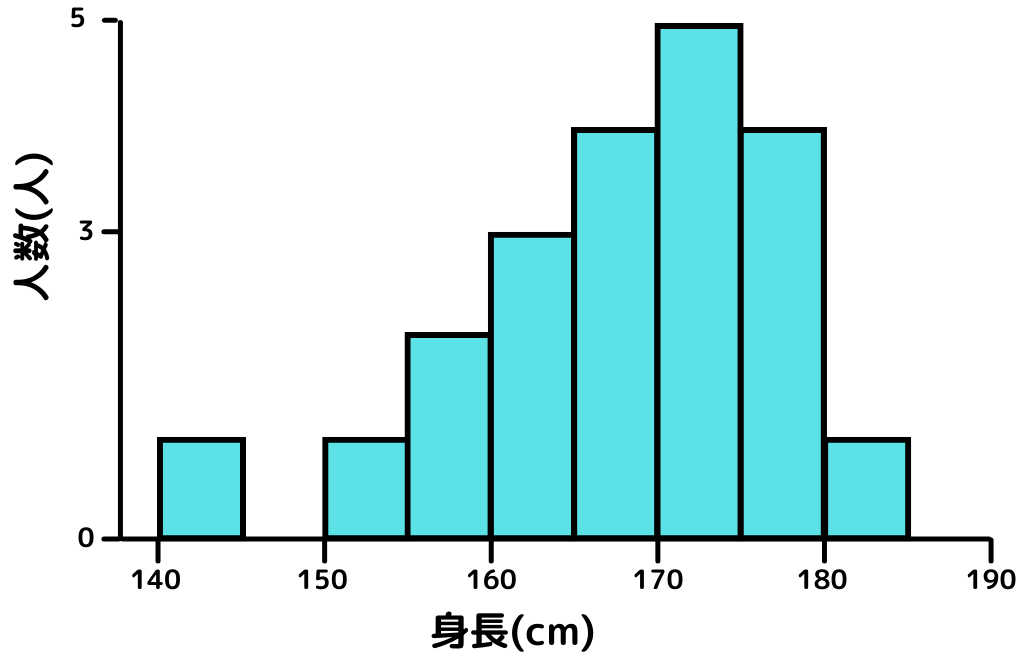
170 cm以上175 cm未満が一番多く、左の裾が長い分布ということが一目でわかりますね。
DS９６：クロス集計表を作成し、属性間のデータの偏りを把握できる
次は「クロス集計表」を作成して、意味を読み取れるようになりましょう。
こちらも「クロス集計表」とは何か？から見ていきます。
クロス集計表
クロス集計表
2つの因子（属性）を持つデータをかけ合わせて集計する方法のこと。
最終的には以下のような表が出来上がる。
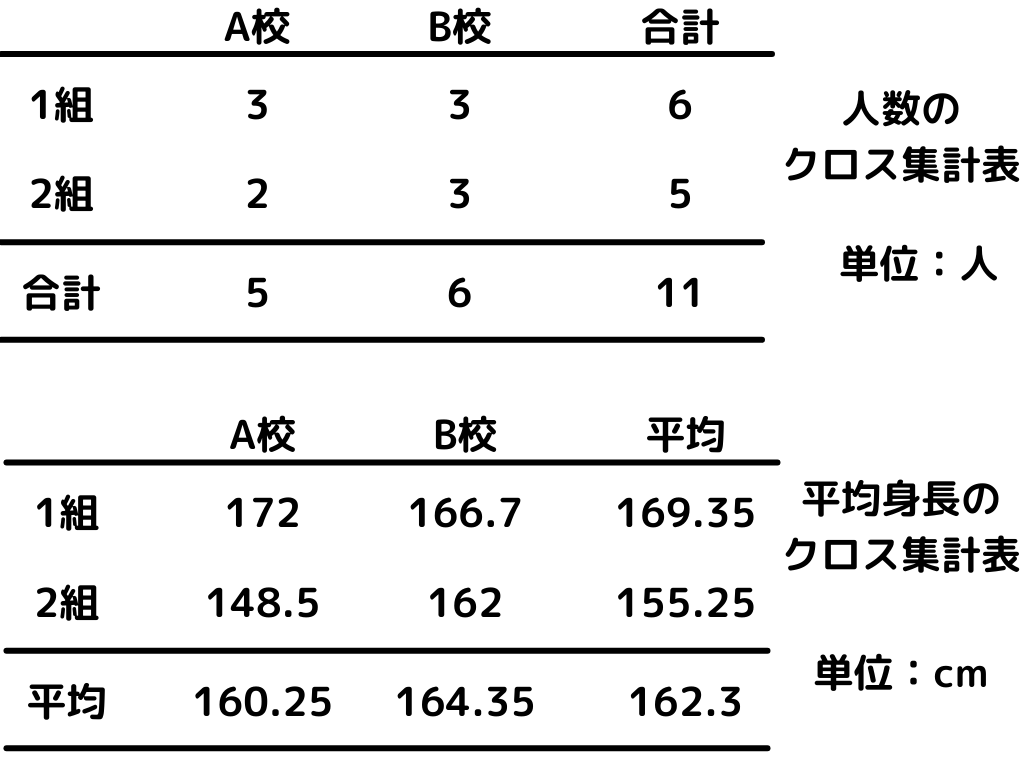
以下のデータを例にして、クロス集計表を作成し、属性間の偏りを見ていきましょう。
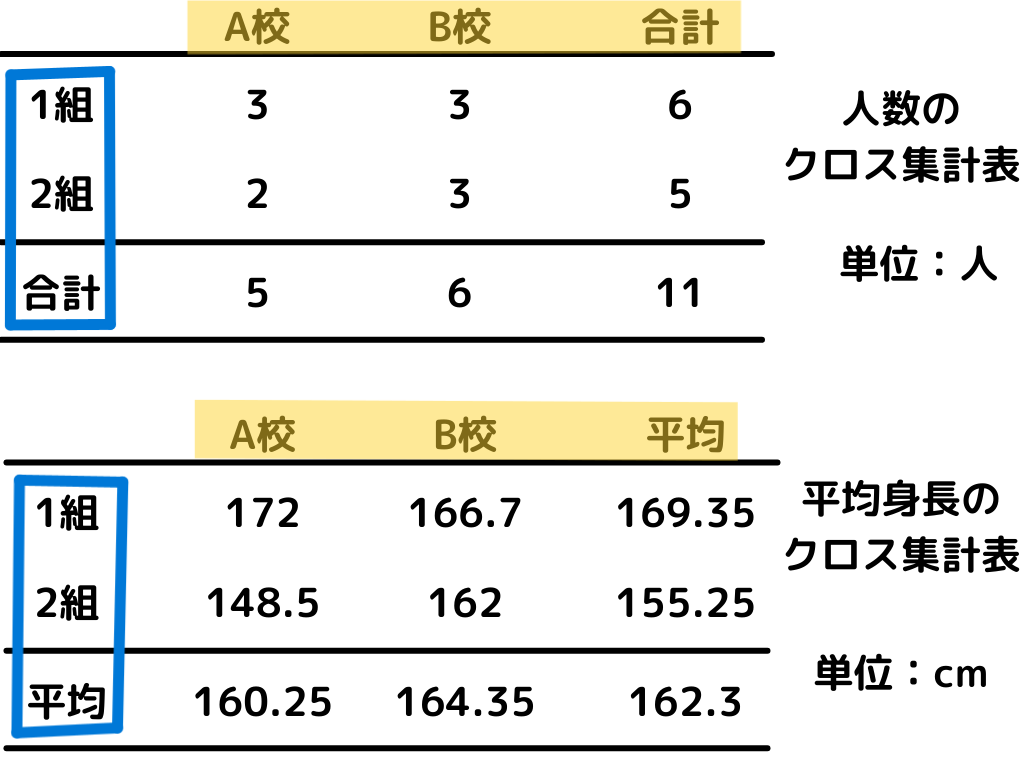
１．クロス集計表の「列の属性（表頭：黄色）」と「行の属性（表側：青色）」を定める
クロス集計表の図で示すと、以下の部分のこと。
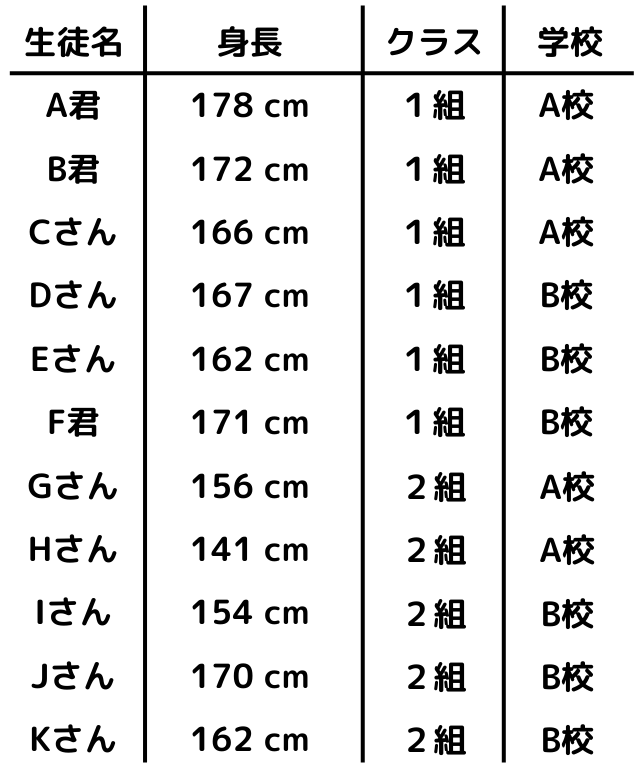
今回のデータの属性は「学校」と「クラス」です。
２．行と列の属性を掛け合わせて、両方を満たす計算を行う
例えば「人数」と「平均身長」を調べたい時は、以下のような表になります。
「人数」はそれぞれの人数を数えればいいだけですね。
「平均身長」は、行と列両方を満たす人たちの平均身長を計算します。
すると表からは、
・全体の平均身長が162.3 cmである
・平均身長が一番高いのは「A校」の「1組」である
・人数が一番少ないのは「A校」の「2組」である
などが分かりますね。
DS９７：量的変数の散布図を描き、2変数の関係性を把握できる
次は「散布図」を作成して、意味を読み取れるようになりましょう。
同じく「散布図」とは何か？から見ていきます。
散布図
散布図
二つの量的変数があった際に、それぞれのデータの点を打ったグラフのこと。
二つの量的変数の関係性を把握したいときに用いる。
以下のグラフのイメージ
以下のデータを例にして、散布図を作成し、二変数の関係性を見ていきましょう。
今回の場合、身長・体重のデータを生徒ごとに打っていけばOKです。
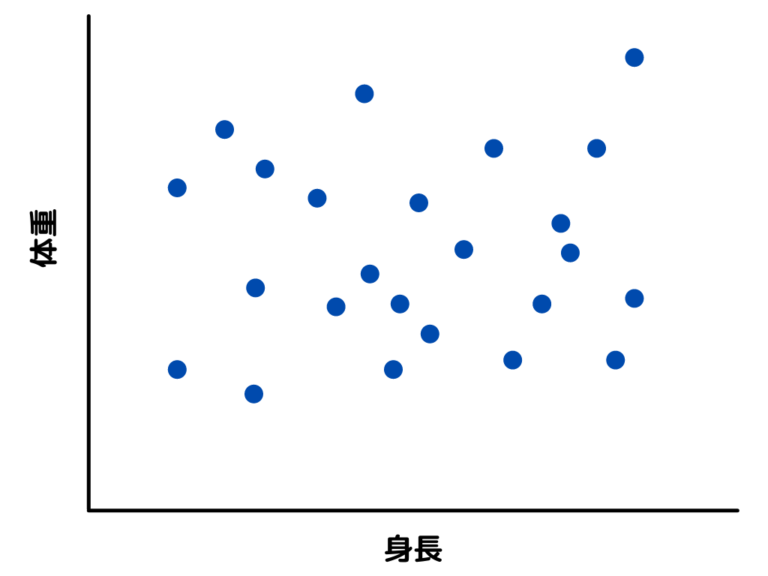
すると、以下のようなグラフが得られます。
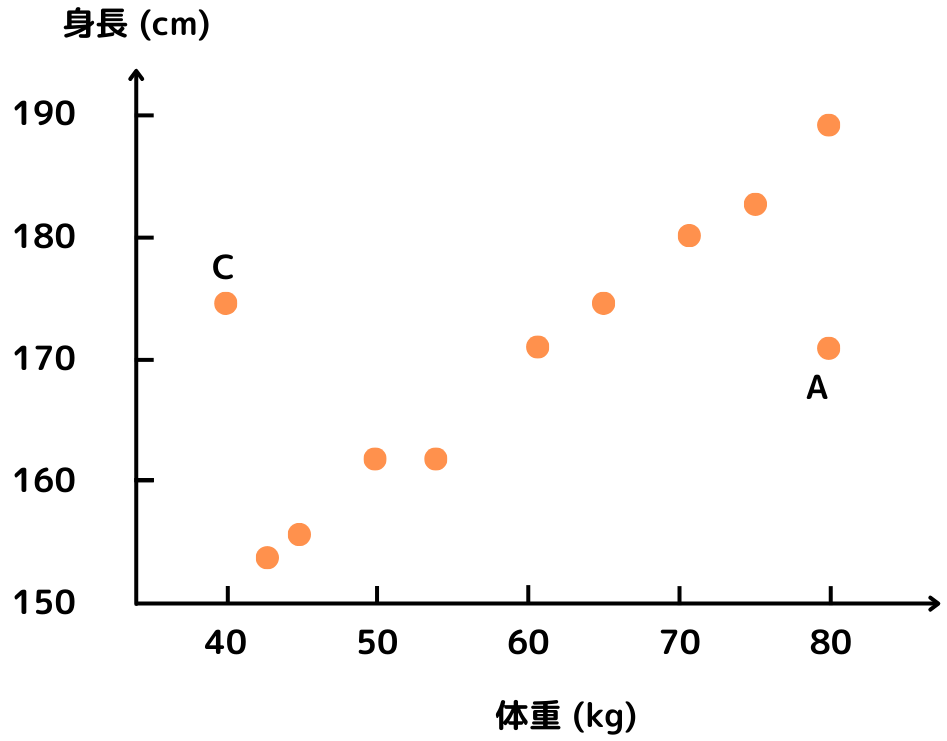
この散布図を見ると、身長が増えるたびに体重が増えていくことが分かりますね。
少し外れ値（A君やCさん）はありますが、おおむね「体重が増えれば身長が高くなる」という傾向は掴めるでしょう。
DS１１２：因果効果を推定したい場合、交絡因子の考慮が重要
難しい言葉が並んでいますね。
まずは用語の解説からしていきます。
因果効果・交絡因子
因果効果
ある要因が結果に与えている影響のこと
図にすると以下のようなイメージ。
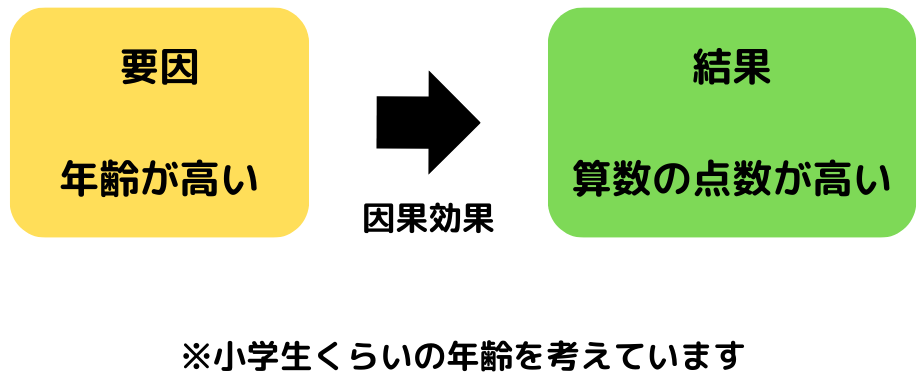
このように要因（年齢が高い）が原因となって、結果（年収が高い）に影響を与えていれば「因果効果」があるということになります。
交絡因子
「要因」と「結果」両方に影響を与える因子のこと。
一つ注意したいのは、以下のような例は交絡因子ではない、という点です。
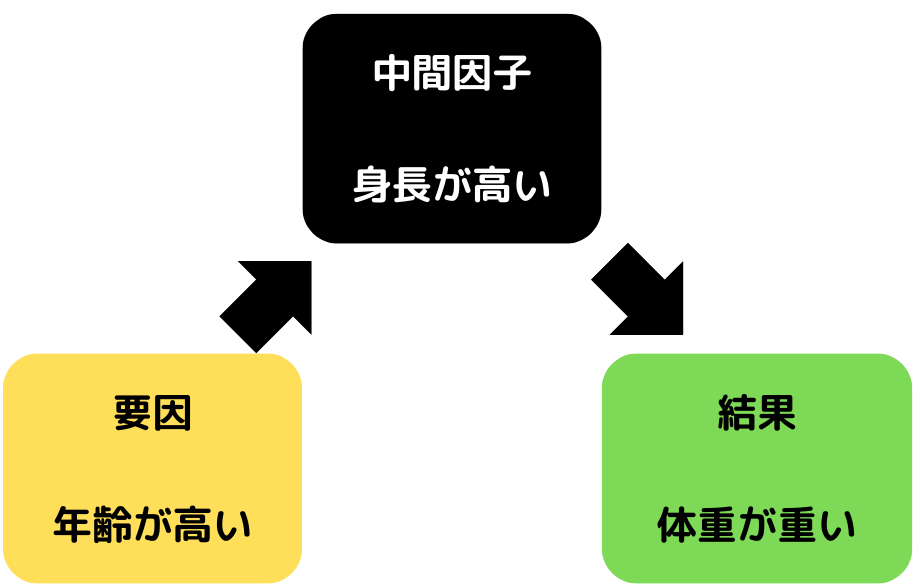
上図のような例は「中間因子」と呼びます。
要因「年齢が高い」がゆえに中間因子「身長が高く」なる傾向にありますね。
（高学年になるほど身長が伸び、体重も増えやすい）
さらに中間因子「身長が高い」結果、「体重が重く」なるという関係になっていますね。
このように要因⇒因子⇒結果の関係になる因子のことを「中間因子」といいます。
では以下の場合はどうでしょうか。
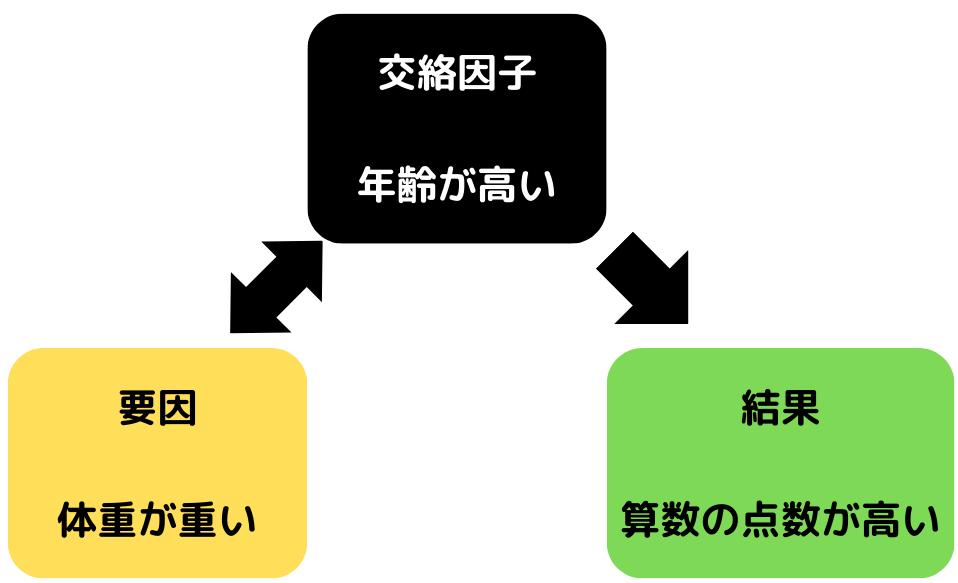
この場合だと、要因「体重が重い」がゆえに交絡因子「年齢が高く」なり、さらに交絡因子「年齢が高い」結果、「算数の点数が高く」なる、とは考えにくいですよね。
しかし、「年齢が高い」は「体重が重い」と関連がありそうです。
さらに「年齢が高い」は「算数の点数が高い」に影響を及ぼしそうですね。
この時の「年齢が高い」を交絡因子と言います。
中間因子と交絡因子は混同しやすいので、注意しましょう。
まとめ
今回は「データの可視化・関係性」などを解説してきました。
以下の項目を説明できるようになっているでしょうか？
・ヒストグラム
・クロス集計表
・散布図
・因果効果
・交絡因子
DS検定は覚える内容が多いです。
一つ一つを細部まで見るというよりは、広く浅く見ていくことが重要かと思います。
DS検定を取得して、データサイエンティストやAI関連の仕事への道を開きましょう！
次回はデータの「バイアス」「サンプリング」などについて解説していきます。
ではまた～
DS検定の続きの解説は以下のページからどうぞ！
コメント