※本記事はアフィリエイト広告を含んでいます

どーも、りけーこっとんです。
DS検定の勉強をしよう!と思ったは良いものの、こんな悩みはありませんか?

DS検定ってどうやって勉強すればいいの?
DS検定の勉強の仕方が分からない…

本で勉強するのは分かるけど、高いなぁ…
無料で単語解説されているサイトとかないかな?

DS検定は、始まったばかりの試験だから、対策法とか分からないよね。
じゃあ、このサイトで出題範囲の内容を押さえていこう~
DS検定の解説をすぐ見たいよ!という方は、以下から最初の解説に飛べます。


今回はスキルチェックリスト
「DS5:母平均と標本平均、不偏分散と標本分散の違いを説明できる」から
「DS7:相関関係と因果関係の違いを説明できる」を解説していくよ~
本サイトでは超重要項目、重要項目、覚えておきたい項目と表記を分けますので、勉強時の参考にしてみてください。
DS検定って、そもそもどんな資格?という方は以下の記事をご覧くださいね。
試験範囲は以下の二つから出題されます。
・スキルチェックリスト
・数理、データサイエンス、AI(リテラシーレベル)モデルカリキュラム
本内容は以下の書籍を参考に作成しております。
なお、本サイトはDS検定の合格を保証するわけではありませんので、ご了承ください。
では早速、内容に入っていきましょう!
※「DS○○:」項目の文章は独自に短縮して表現しております
目次
DS5:母平均と標本平均、不偏分散と標本分散の違いを説明できる
この項目は以下の四つを説明できますか?という内容。
・母平均
・標本平均
・不偏分散
・標本分散
これらの単語を説明する前に、「母集団」「標本」という言葉を知っておく必要があります。
母集団:
データ分析などを行うときに、対象になるデータ全体のこと。
(例)
・A県の高校生の平均身長を知りたい!
⇒A県の高校生全員の身長データ
・日本でYouTubeを見ている人の割合を知りたい!
⇒日本人全員へのアンケート結果
具体例を見ると分かる通り、データを集めるのが大変そうですよね。
場合によっては不可能なものもあります。
そこで、実際にデータを集めるときには「標本」という概念が重要。
標本:
母集団の中から、抽出したいくつかのデータのこと。
実際には「標本」を使って、データ収集したり分析することが多いです。
母集団と標本の関係について図にすると以下の通り。
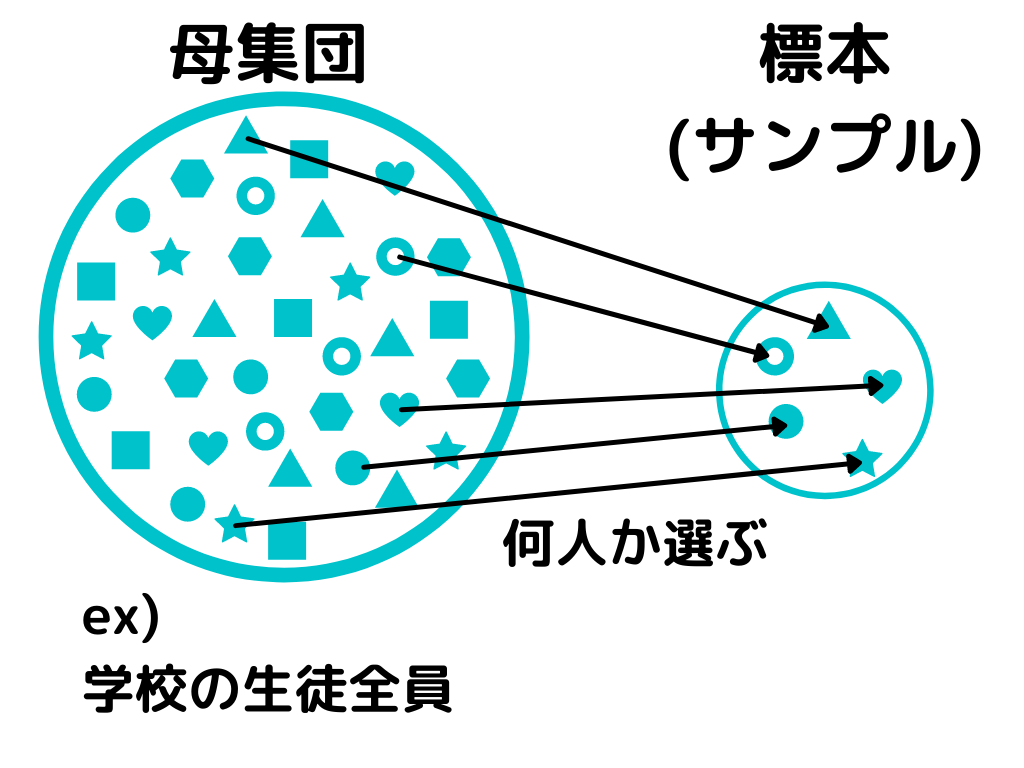
母平均と標本平均
母平均の「母」は母集団という意味です。
このことから、母平均が何か想像できる人もいるのではないでしょうか。
母平均:
母集団全体での平均のこと。
しかし前述の通り、母平均を求めるのは、そもそもデータを集めるのが大変です。
そこで「標本平均」があります。
標本平均:
標本での平均のこと。母平均の推定に用いられる。
母平均を求めるのは無理でも、標本平均なら求められます。
標本平均から母平均を推定することで、母平均を求めるという手法が用いられるようですね。
※DS検定において数学的な導出・計算は重要でないので、省略します
不偏分散と標本分散
不偏分散と標本分散に関しては、初めましての人も多いのではないでしょうか。
分かりやすそうな「標本分散」から説明していきましょう。
標本分散:
標本での分散のこと。\(\displaystyle s^2\)
得られたデータ(標本)の平均を\(\displaystyle \bar{x}\)、一つ一つのデータを\(\displaystyle x_k\)、標本の数を\(\displaystyle n\)とすると以下の式で定義できる。
\(\displaystyle s^2 = \frac{1}{n}\sum_{k=1}^{n}(x_k – \bar{x})^2\)
いわゆる普通の分散と同じ式ですね。
ちなみに\(\displaystyle \sum_{k=1}^{n}\)というのは、標本\(\displaystyle n\)個全てのデータを足すよ、という意味です。
次に不偏分散を見ていきましょう。
不偏分散:
母集団の分散(母分散)を推定するために用いる。\(\displaystyle U^2\)
得られたデータ(標本)の平均を\(\displaystyle \bar{x}\)、一つ一つのデータを\(\displaystyle x_k\)、標本の数を\(\displaystyle n\)とすると以下の式で定義できる。
標本平均とほぼ同じ式ということが分かると思います。
異なるのは標本の数\(\displaystyle n\)個ではなく、\(\displaystyle n-1\)で割るということ。
なぜ\(\displaystyle n-1\)で割るかまでは、DS検定で問われないと思うので、割愛します。
気になる方は以下を参考にしてみてください。
いちばんやさしい医療統計|不偏分散がn-1で割る理由を簡単に!
DS6:標準正規分布の平均と分散を説明できる
この項目は、標準正規分布を説明できるということが重要です。
そのためにまず、正規分布について触れておきましょう。
正規分布
正規分布:
統計学で用いられる、最も基本的な分布の一つ。
分布の形(山の形)が「平均」と「標準偏差」で決まる。
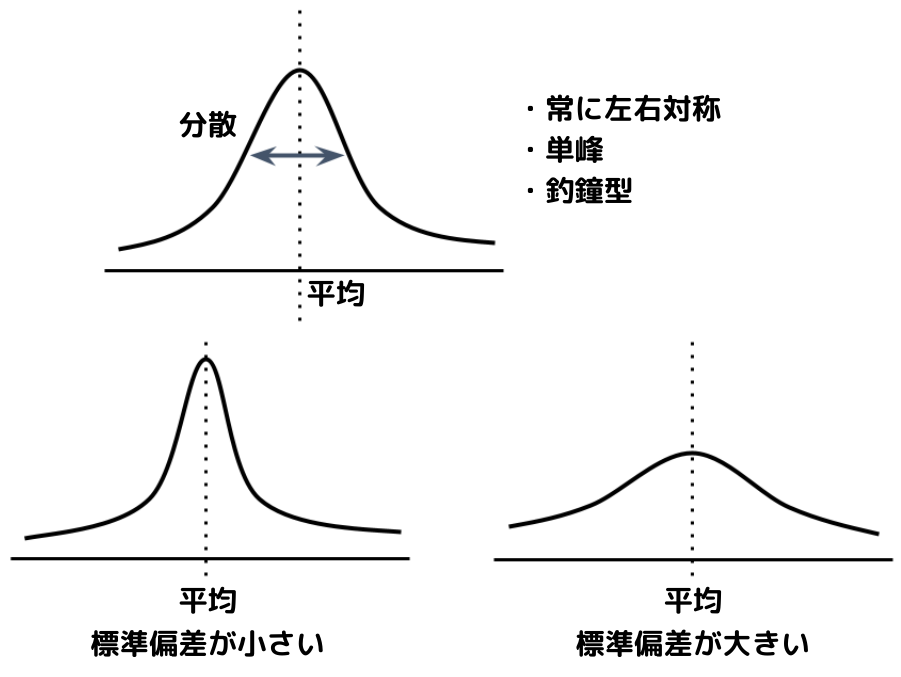
正規分布と言われたら、上のような形をイメージできるといいでしょう。
正規分布の形を表せる式もあります。
以下に正規分布の式\(\displaystyle f(x)\)を一応示しますが、DS検定で問われることは無いと思います。
$$f(x) = \frac{1}{\sqrt{2\pi \sigma^2}}\exp(-\frac{(x-\mu)^2}{2\sigma^2})$$標準正規分布
正規分布に「標準」がつくと、どうなるのでしょうか。
標準正規分布:
平均が0、分散が1の正規分布のこと。
以下の式でzスコアを算出することで、正規分布を標準正規分布に変換できる。
各データを\(\displaystyle x\)とすると
\(\displaystyle zスコア = \frac{x-平均}{標準偏差}\)
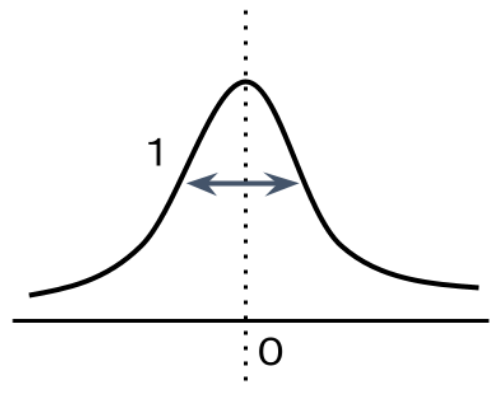
データ分析、機械学習の分野では収集データを「標準正規分布」に直すことが行われます。
zスコアの計算は「標準化・正規化」とも呼ばれていて、数値のスケールを合わせるために行われるんですね。
例えば身長のデータは140~200 (cm)くらいに数字が収まります。
体重は30~90 (kg)といったところでしょうか。
体重は2桁であるのに対し、身長は3桁の数字ですね。
これをそのままAIやデータ分析に使ってしまうと、上手くできないことが多いんです。
これからAIやデータサイエンスなどに関わる方は、必須の知識と言えるでしょう。

DS7:相関関係と因果関係の違いを説明できる
相関関係と因果関係は、似ているようで違う言葉です。
日本語の意味としては、「相関」「因果」どのような意味なのでしょうか。
因果:
原因と結果を意味する用語
(引用:Wikipedia|因果)
相関:
一方が変化すれば他方も変化するように相互に関係しあうこと
(引用:Wikipedia|相関)
分かるような分からないような?
それぞれの違いを意識しながら、解説していきます。
因果関係
因果関係:
AとBの現象や事柄が原因と結果の関係になっている。
具体例を見てみましょう。
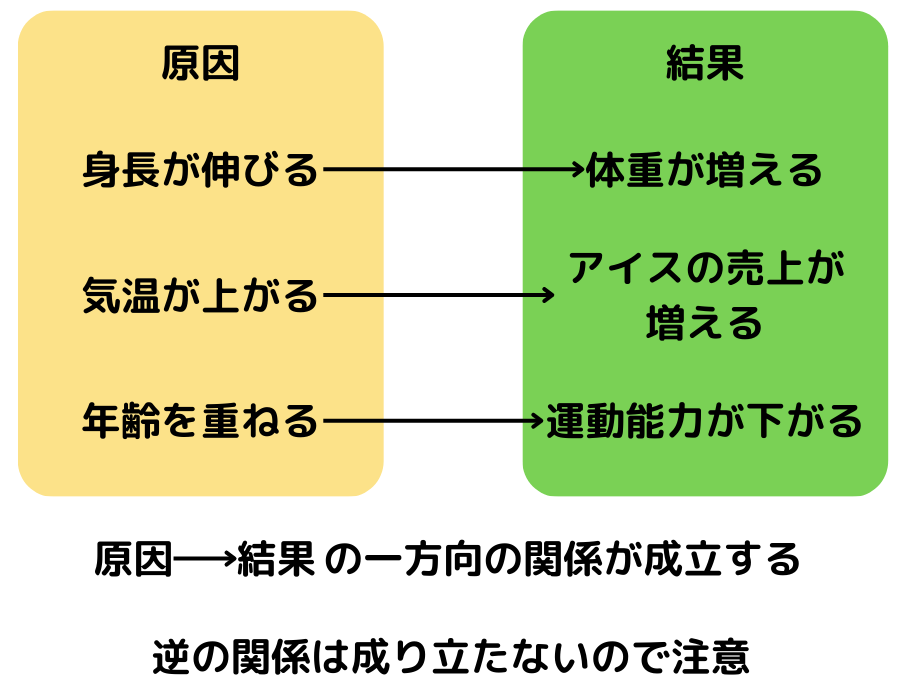
1.「身長(A)」が伸びると「体重(B)」が増える
2.「気温(A)」が上がれば「アイスの売り上げ(B)」が伸びる
3.「年齢を重ねる(A)」と「運動能力(B)」が低下する
これらは全てA(原因)⇒B(結果)という関係になっていそうですよね。
B(原因)⇒A(結果)ということもありません。
例えば3で「運動能力(B)が低下した」からといって、「年齢を重ねている(A)」と言えるでしょうか。
もしかしたら、ケガをしたのかもしれませんよね。
病気になったのかも。
このように、A(原因)⇒B(結果)という関係になっていること(逆は成り立たない)を因果関係があるといいます。
相関関係よりも、狭い意味になりますね。
相関関係
相関関係:
AとBの現象・事柄に何かしらの関係性があること。
必ずしもAとBが原因と結果になっているわけではない。
片方が増えると、もう片方も増えることを「正の相関がある」
片方が増えると、もう片方は減ることを「負の相関がある」 といいます。
具体例を見てみましょう。
1.「理科(A)」の点数と「数学(B)」の点数には正の相関がある
2.「身長(A)」と「体重(B)」には正の相関がある
3.「年齢(A)」と「運動能力(B)」には負の相関がある
ここで重要なのは、必ずしもAとBの事柄は「原因」と「結果」ではないということです。
因果関係では、「原因」と「結果」になっていました。
具体例でも、2と3はA(原因)⇒B(結果)という関係になっていそうですよね。
しかし1はどうでしょうか。
理科の点数が上がることが原因で数学の点数が上がる?
数学の点数が原因で理科の点数が良くなる?
どちらとも言えないですよね。
1の場合も含めて「相関関係」と呼びます。
データを見た時に、単純にAデータが増えたらBデータは増えるか減るかすれば、相関があると言えます。

相関関係と因果関係の位置づけを図にすると以下のようになります。
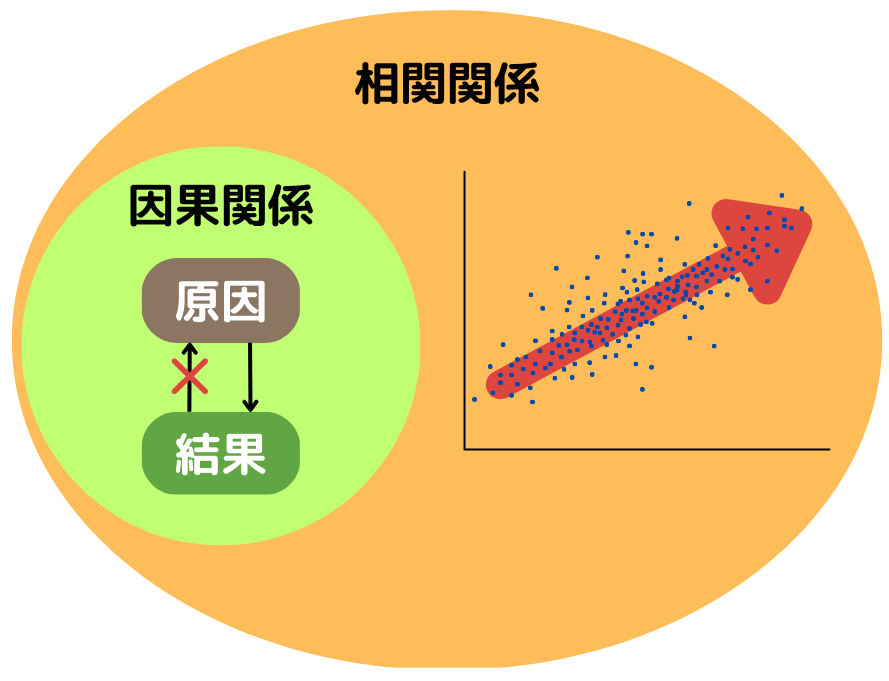
まとめ
今回は「母平均・標準正規分布・相関と因果」などを解説してきました。
以下の項目を説明できるようになっているでしょうか?
・母平均
・標本平均
・不偏分散
・標本分散
・正規分布
・標準正規分布
・因果関係
・相関関係
DS検定は覚える内容が多いです。
一つ一つを細部まで見るというよりは、広く浅く見ていくことが重要かと思います。
DS検定を取得して、データサイエンティストやAI関連の仕事への道を開きましょう!
次回は「尺度の種類」「相関係数」などについて解説していきます。
ではまた~

DS検定の続きの解説は以下のページからどうぞ!


![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/214d380e.96fa3830.214d380f.9c4125c0/?me_id=1213310&item_id=20632239&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F8326%2F9784297128326_1_2.jpg%3F_ex%3D240x240&s=240x240&t=picttext)








