※本記事はアフィリエイト広告を含んでいます
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/214d380e.96fa3830.214d380f.9c4125c0/?me_id=1213310&item_id=20632239&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F8326%2F9784297128326_1_2.jpg%3F_ex%3D240x240&s=240x240&t=picttext "[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]")
どーも、りけーこっとんです。
DS検定の勉強をしよう！と思ったは良いものの、こんな悩みはありませんか？
DS検定ってどうやって勉強すればいいの？
DS検定の勉強の仕方が分からない…
本で勉強するのは分かるけど、高いなぁ…
無料で単語解説されているサイトとかないかな？
DS検定は、始まったばかりの試験だから、対策法とか分からないよね。
じゃあ、このサイトで出題範囲の内容を押さえていこう～
DS検定の解説をすぐ見たいよ！という方は、以下から最初の解説に飛べます。
今回はスキルチェックリスト
「DS１３：指数・log関数を理解し、対数グラフを使い分けられる」と
「DS１４：ベイズの定理を説明できる」を解説していくよ～
本サイトでは超重要項目、重要項目、覚えておきたい項目と表記を分けますので、勉強時の参考にしてみてください。
DS検定って、そもそもどんな資格？という方は以下の記事をご覧くださいね。
試験範囲は以下の二つから出題されます。
・スキルチェックリスト
・数理、データサイエンス、AI（リテラシーレベル）モデルカリキュラム
本内容は以下の書籍を参考に作成しております。
なお、本サイトはDS検定の合格を保証するわけではありませんので、ご了承ください。
では早速、内容に入っていきましょう！
※「DS○○：」項目の文章は独自に短縮して表現しております
DS１３：指数・log関数(対数関数)を理解し、対数グラフを使い分けられる
まずは指数関数とlog関数（対数関数）が、どういう式なのか見ていきましょう。
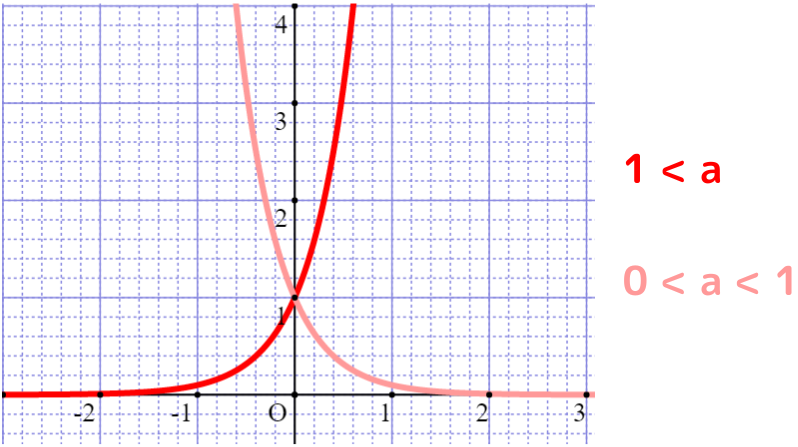
指数関数
指数関数
「定数aをx回掛け算した」という意味の関数。
aを「底」、xを「指数」という。
\(\displaystyle y = a^x\)
a(底)を10としたときのグラフ
対数関数
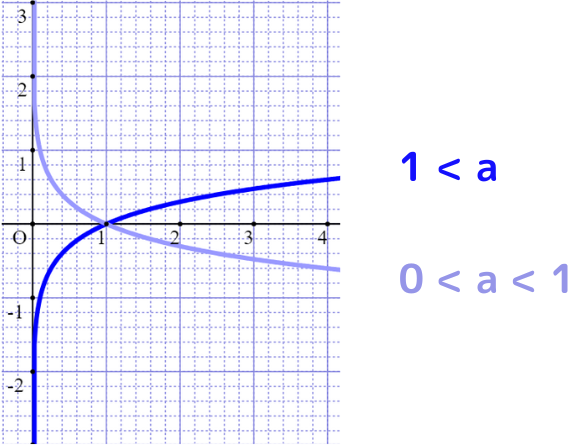
log関数（対数関数）
「定数aを何回掛け算したらxになるか」を求める関数。
aを「底」、xを「真数」という。
・底が10の対数を「常用対数」
・底がe(ネイピア数)の対数を「自然対数」という。
\(\displaystyle y = log_{a}x\)
a(底)を10としたときのグラフ
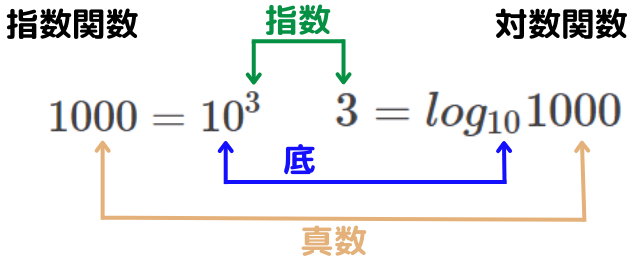
指数関数・対数関数の関係
指数関数とlog関数の式の関係としては、以下の通りです。
また、指数関数と対数関数の底を同じ10にした時のグラフの関係は以下の通り。
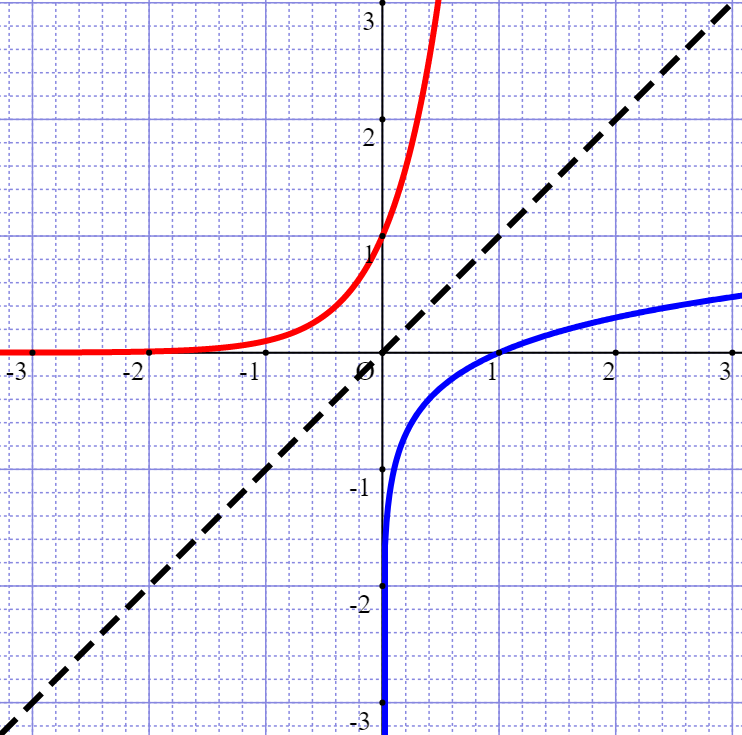
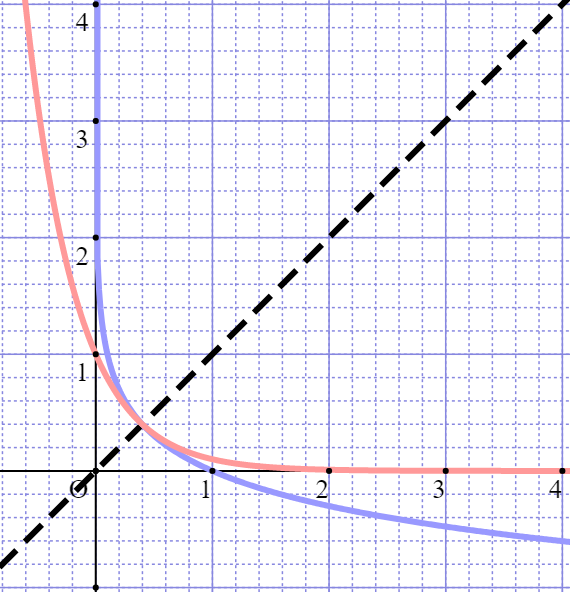
指数関数と対数関数には、
底が同じならば\(\displaystyle y = x\)の直線に対して対称になる
という性質がありますので、合わせて覚えておきましょう。
片対数グラフ
片対数グラフ
グラフの軸で、片方が対数スケールになっているグラフのこと。
指数関数に使いやすい。
出典：https://ja.wikipedia.org/wiki/%E7%89%87%E5%AF%BE%E6%95%B0%E3%82%B0%E3%83%A9%E3%83%95
式変形をして、なぜ片方だけ対数スケールにすると良いのかを解説しますね。
指数関数\(\displaystyle y = 10^{x+3}\)を考えます。
まずは両辺にlogを取りましょう。
\(\displaystyle log_{10}y = log_{\color{red}{10}}\color{red}{10}^{x+3}\)
対数は「底」と「真数の中の累乗の底」が一致するとき（赤字部分）、logが消せるので
\(\displaystyle log_10 (y) = x+3\)
すると、\(\displaystyle x+3\)の関数が出てきましたね。
\(\displaystyle y\)に関しては\(\displaystyle log_{10}y\)になっています。
つまりy軸（縦軸）を対数スケールにすれば、\(\displaystyle x+3\)という簡単な直線の形になるわけです。
両対数グラフ
両対数グラフ
グラフの軸の両方が対数スケールになっているグラフのこと。
\(\displaystyle y = x^2\)のように累乗の関数に使いやすい。
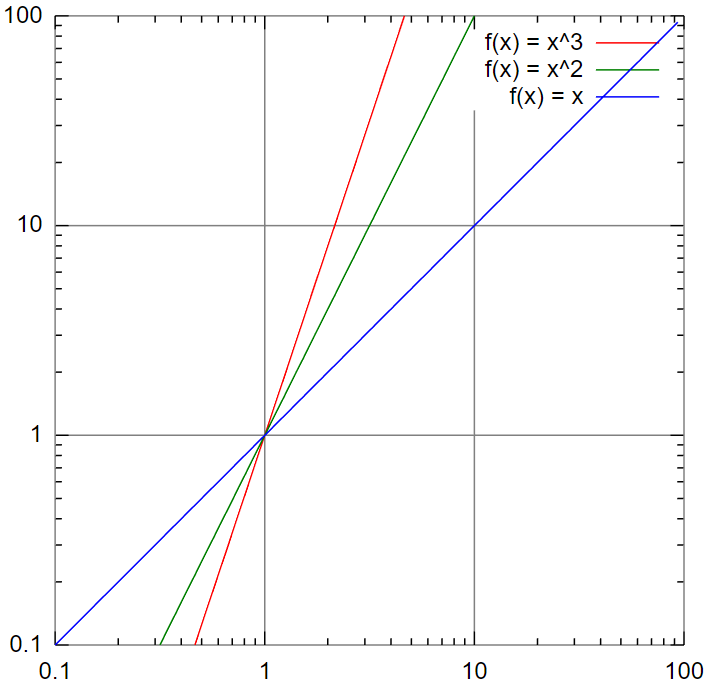
出典：https://ja.wikipedia.org/wiki/%E4%B8%A1%E5%AF%BE%E6%95%B0%E3%82%B0%E3%83%A9%E3%83%95
式変形をして、なぜ両方の軸を対数スケールにすると良いのかを見ていきましょう。
累乗関数\(\displaystyle y = x^2\)を考えます。
まずは両辺にlogを取りましょう。
\(\displaystyle log_{10} (y) = log_{10}x^{\color{red}{2}}\)
対数の「真数の中の累乗の指数(赤字部分)」は、logの前に出せるので
\(\displaystyle log_{10}y = 2log_{10}x\)
すると\(\displaystyle log_{10}y, log_{10}x\)を普通の\(\displaystyle y, x\)と考えれば、\(\displaystyle y = 2x\)の関数が出てきましたね。
\(\displaystyle y, x\)の両方が\(\displaystyle log_{10}y, log_{10}x\)になっています。
つまりx, y軸の両方を対数スケールにすれば、\(\displaystyle 2x\)という簡単な直線の形になるわけです。
DS１４：ベイズの定理を説明できる
ベイズの定理
以下の定義式で表される。ベイズ統計学の最も基本部分。
P(A|B)：事後確率（Bであることが分かった場合にAになる確率）
P(B)：事前確率（Bが起こる確率）
P(B|A)：尤度（Aであることが分かった場合にBになる確率）
P(A)：正規化定数（Aが起こる確率）
式だけではわからないと思うので、例題を一つ解きましょう。
あなたはお菓子をX・Y・Z社から仕入れて販売しています。それぞれの会社からの仕入れ量の割合は20・30・50%です。また、それぞれの会社は不良品を6・5・4%の確率で出してしまいます。
ある日、あなたは不良品を見つけました。この不良品がY社の不良品である確率は何％でしょうか。
求めたいのは「不良品がY社のお菓子である確率」なので、これをP(A|B)とします。
P(A|B)の理解の仕方としては、
「B：不良品が発生する」ということが分かった場合、「A：Y社のお菓子である」確率ですね。
なのでP(B)、P(B|A)、P(A)はそれぞれ
P(B)：不良品が発生する確率（全社に渡って）
P(B|A)：Y社のお菓子であった場合に、不良品になる確率
P(A)：Y社のお菓子である確率
となります。
それぞれの確率を求めていきましょう。
P(A)はY社のお菓子である確率なので、30%(0.3)ですね。
P(B|A)は、Y社のお菓子の時に不良品になる確率なので、掛け算になります。 $$P(B|A) = 0.3 \times 0.05 = 0.015$$P(B)は不良品の発生する確率ですね。これはX・Y・Z社全ての不良品確率を足さなければいけません。
Y社の不良品確率を求めた方法で、X・Z社も求めます。
以上３つの確率を求めたことで、ベイズの定理が使えます。
$$P(B|A) = \frac{0.015\times0.3}{0.047} = 0.0957… \neq 0.096$$まとめ
今回は「指数関数・対数関数・ベイズの定理」などを解説してきました。
以下の項目を説明できるようになっているでしょうか？
・指数関数
・対数関数
・片対数グラフ
・両対数グラフ
・ベイズの定理
DS検定は覚える内容が多いです。
一つ一つを細部まで見るというよりは、広く浅く見ていくことが重要かと思います。
DS検定を取得して、データサイエンティストやAI関連の仕事への道を開きましょう！
次回は「ベクトル」「内積」「行列」などについて解説していきます。
ではまた～
DS検定の続きの解説は以下のページからどうぞ！
コメント