※本記事はアフィリエイト広告を含んでいます
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/214d380e.96fa3830.214d380f.9c4125c0/?me_id=1213310&item_id=20632239&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F8326%2F9784297128326_1_2.jpg%3F_ex%3D240x240&s=240x240&t=picttext "[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]")
どーも、りけーこっとんです。
DS検定の勉強をしよう！と思ったは良いものの、こんな悩みはありませんか？
DS検定ってどうやって勉強すればいいの？
DS検定の勉強の仕方が分からない…
本で勉強するのは分かるけど、高いなぁ…
無料で単語解説されているサイトとかないかな？
DS検定は、始まったばかりの試験だから、対策法とか分からないよね。
じゃあ、このサイトで出題範囲の内容を押さえていこう～
DS検定の解説をすぐ見たいよ！という方は、以下から最初の解説に飛べます。
今回はスキルチェックリスト
「DS１０：代表的な確率分布を５つ説明できる」から
「DS１１：二項分布の試行回数が増えるとどうなるか知っている」を解説していくよ～
本サイトでは超重要項目、重要項目、覚えておきたい項目と表記を分けますので、勉強時の参考にしてみてください。
DS検定って、そもそもどんな資格？という方は以下の記事をご覧くださいね。
試験範囲は以下の二つから出題されます。
・スキルチェックリスト
・数理、データサイエンス、AI（リテラシーレベル）モデルカリキュラム
本内容は以下の書籍を参考に作成しております。
なお、本サイトはDS検定の合格を保証するわけではありませんので、ご了承ください。
では早速、内容に入っていきましょう！
※「DS○○：」項目の文章は独自に短縮して表現しております
DS１０：代表的な確率分布を５つ説明できる
以前の記事を読んでくださっている方は「正規分布」を聞いたことがあると思います。
その際に、正規分布は代表的な確率分布という説明をしました。
実は正規分布以外にも、統計学には確率分布の種類がいくつもあります。
その中でも基本的な分布に触れていきましょう。
確率分布は大きく以下の二種類に分かれます。
どちらも図で表現すると、山のようなグラフになるので区別しにくいです。
図で形を覚えつつ、離散型・連続型どちらに分類されるのかも覚えておくといいでしょう。
またDS検定では、それぞれの分布の「期待値」と「分散」を求める式も覚えておくと確実ですね。
ではまず、連続型確率分布から解説します。
正規分布
正規分布は、統計学で最も基本的な分布といっていいでしょう。
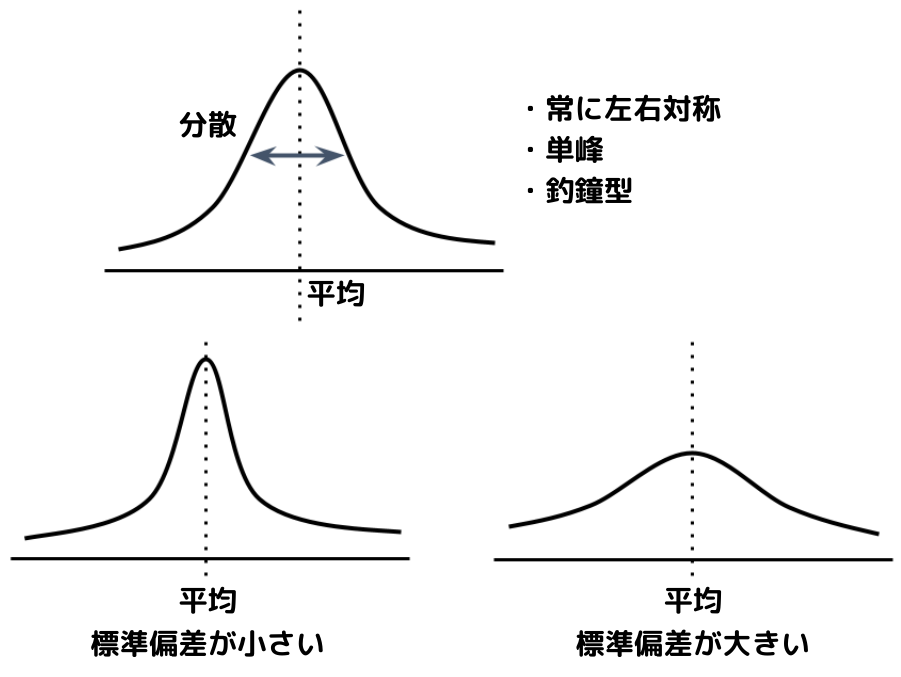
正規分布：
統計学で用いられる、最も基本的な連続型確率分布の一つ。
分布の形（山の形）が「平均」と「標準偏差」で決まる。
正規分布の形を表せる式もあります。
この山の形を式にしたものを「確率密度関数」というので覚えておきましょう。
※連続型確率分布にのみ出てくる用語
以下に正規分布の確率密度関数\(\displaystyle f(x)\)を一応示しますが、DS検定で問われることは無いと思います。
$$f(x) = \frac{1}{\sqrt{2\pi \sigma^2}}\exp(-\frac{(x-\mu)^2}{2\sigma^2})$$連続一様分布
統計学には「一様分布」というものがあります。
一様分布は、確率変数が連続的か離散的かで、呼び方が変わるんですね。
それに伴って、平均値や分散の算出する式が異なります。
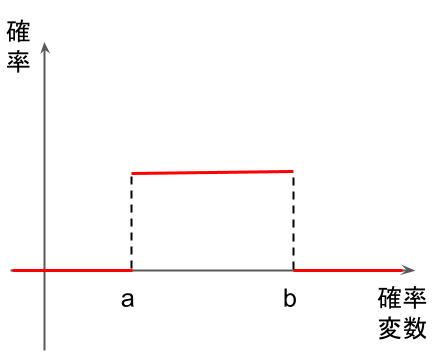
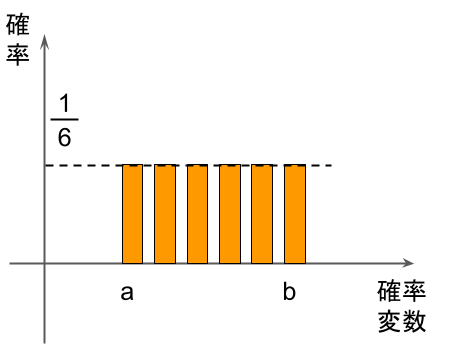
連続一様分布：
確率変数がどんな値でも、確率密度関数が一定値を取る連続型確率分布。
期待値と分散の式
\(\displaystyle E(x) = \frac{a+b}{2}\)
\(\displaystyle V(x) = \frac{(b-a)^2}{12}\)
図のようにaとbの間では、確率変数がどんな値を取ろうが同じ確率になります。
指数分布
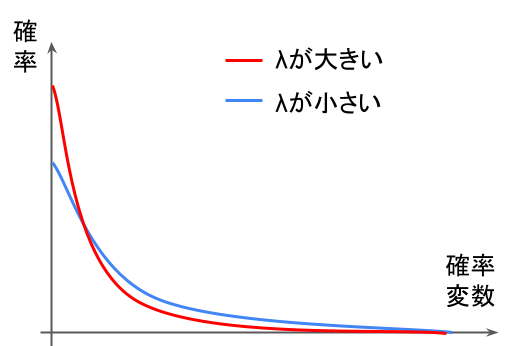
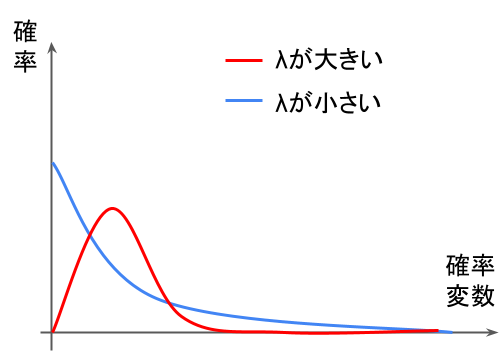
指数分布：
ある時間で平均\(\displaystyle \lambda\)回起こる現象が、次に起こるまでの時間\(\displaystyle x\)を表した連続型確率分布。
期待値と分散の式
\(\displaystyle E(x) = \frac{1}{\lambda}\)
\(\displaystyle V(x) = \frac{1}{\lambda^2}\)
例を一つ考えてみましょう。
1時間で平均10人訪れる店に、5分後お客さんが来る確率（5分間の間に来店はなし）
この確率分布は指数分布に従います。
定義分に対応させると、
・ある時間で平均\(\displaystyle \lambda\)回起こる現象
⇒1時間で平均10人訪れる
・次に起こるまでの時間\(\displaystyle x\)
⇒5分後お客さんが来る
というわけですね。
以下からは、離散型確率分布を解説していきます。
二項分布
連続一様分布：
試行をn回行った時の成功回数が従う離散型確率分布。
以下の条件を満たさなければならない。
・試行結果が「成功」「失敗」のどちらかのみ
・試行をn回繰り返す
・試行同士は独立
期待値と分散の式
\(\displaystyle E(x) = np\)
\(\displaystyle V(x) = np(1-p)\)
例を一つ考えてみましょう。
コインを5回投げて、2回表が出る確率
この確率分布は二項分布に従います。
二項分布を満たす条件を考えてみると、
・試行結果が「成功」「失敗」のどちらかのみ
⇒コインの「表」「裏」を成功 or 失敗に対応付けられます
・試行をn回繰り返す
⇒コインを複数回投げているので、n回繰り返せます
・試行同士は独立
⇒1回目「表」が出たという結果が、2回目のコイントスに影響しません
というわけですね。
離散一様分布
前の項でも触れましたが、一様分布は確率変数が連続的か離散的かで、呼び方が変わります。
それに伴って、平均値や分散の算出する式が異なるんでしたね。
離散一様分布：
確率変数がどんな値でも、確率密度関数が一定値を取る離散型確率分布。
（例）サイコロの目
確率変数の取る値の個数\(\displaystyle n\)は6である。
期待値と分散の式
\(\displaystyle E(x) = \frac{n+1}{2}\)
\(\displaystyle V(x) = \frac{(n^2-1)}{12}\)
図のようにaとbの間では、全て同じ確率になっていますね。
サイコロの目（1, 2, 3, 4, 5, 6）といった離散的な数値の時の「一様分布」です。
ポアソン分布
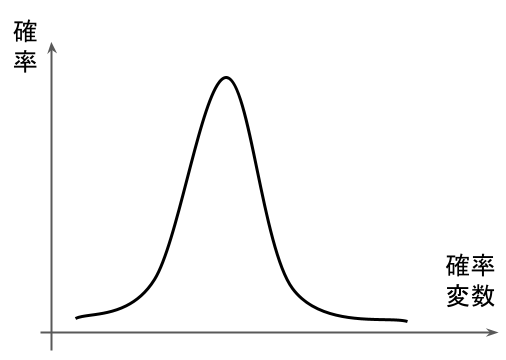
ポアソン分布：
単位時間で平均\(\displaystyle \lambda\)回起こる現象が、ある時間で起こる回数\(\displaystyle x\)を示した離散型確率分布。
期待値と分散の式
\(\displaystyle E(x) = \lambda^2\)
\(\displaystyle V(x) = \lambda\)
例を一つ考えてみましょう。
お祭りのくじは平均して30回で1回のあたりが出ると言われている。
くじを50回引いて、2回当たりが出る確率。
この確率分布はポアソン分布に従います。
定義分と照らし合わせてみると、
平均\(\displaystyle \lambda\)回起こる現象
⇒お祭りのくじは平均して30回で1回のあたりが出る
ある時間で起こる回数\(\displaystyle x\)
⇒くじを50回引いて、2回当たりが出る
というわけですね。
DS１１：二項分布の試行回数が増えるとどうなるか知っている
この項目は、二項分布の内容を掘り下げたものですね。
前の章で解説した二項分布の形は、試行回数nと密接な関係があります。
二項分布の試行回数が増えると、正規分布の形に近づく。
グラフの形は以下のようになる。
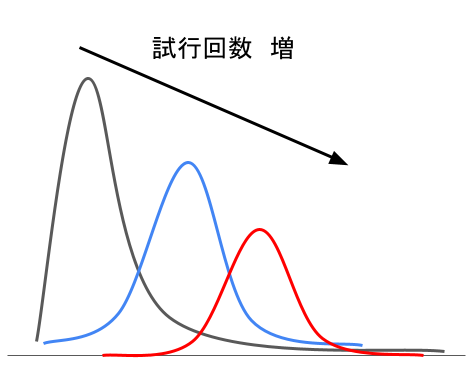
二項分布を正規分布に近づけて、メリットになる点は以下の２点です。
・正規分布は、一つのデータが全体の何％の部分にあるかが分かりやすい (68-95-99.7の法則)
・標準正規分布に正規化しやすく、計算が楽になる
DS１１をまとめると、
「二項分布の試行回数が増えると、正規分布に近づく」
ですね。
まとめ
今回は「確率分布」などを解説してきました。
以下の項目を説明できるようになっているでしょうか？
・正規分布
・連続一様分布
・指数分布
・二項分布
・離散一様分布
・ポアソン分布
・二項分布の試行回数が増えると、正規分布に近づく
DS検定は覚える内容が多いです。
一つ一つを細部まで見るというよりは、広く浅く見ていくことが重要かと思います。
DS検定を取得して、データサイエンティストやAI関連の仕事への道を開きましょう！
次回は「指数関数」「対数関数」「ベイズの定理」などについて解説していきます。
ではまた～
DS検定の続きの解説は以下のページからどうぞ！
コメント