DS検定対策｜データサイエンス力｜片側検定・t検定・z検定を勉強！

※本記事はアフィリエイト広告を含んでいます

最短突破　データサイエンティスト検定（リテラシーレベル）公式リファレンスブック　第2版 [ 菅 由紀子 ] 価格：2,750円（税込、送料無料) (2023/5/18時点) 楽天で購入

どーも、りけーこっとんです。

DS検定の勉強をしよう！と思ったは良いものの、こんな悩みはありませんか？

DS検定の解説をすぐ見たいよ！という方は、以下から最初の解説に飛べます。

本サイトでは超重要項目、重要項目、覚えておきたい項目と表記を分けますので、勉強時の参考にしてみてください。

DS検定って、そもそもどんな資格？という方は以下の記事をご覧くださいね。

DS検定とは？合格ライン・難易度・勉強時間なども解説！

DS検定とはどんな資格なのか、解説しました～。合格ライン・難易度・合格発表・試験日など基本的な内容はもちろん、勉強法・勉強時間・参考書なども解説しています～。

rike-kotton.com

2023.03.05

試験範囲は以下の二つから出題されます。

・スキルチェックリスト
・数理、データサイエンス、AI（リテラシーレベル）モデルカリキュラム

本内容は以下の書籍を参考に作成しております。

最短突破　データサイエンティスト検定（リテラシーレベル）公式リファレンスブック　第2版 [ 菅 由紀子 ] 価格：2,750円（税込、送料無料) (2023/5/18時点) 楽天で購入

なお、本サイトはDS検定の合格を保証するわけではありませんので、ご了承ください。

では早速、内容に入っていきましょう！

※「DS○○：」項目の文章は独自に短縮して表現しております

DS７９：片側検定と両側検定の違いを説明できる

以前の記事で、「検定」については解説しました。

検定の方法には二種類あって、「片側検定」と「両側検定」があります。

それぞれの違いが分かりやすいように、以下のような「帰無仮説」を考えましょう。

帰無仮説は否定したい仮説なので、上記のように立てることがポイント。

ここで、対立仮説には以下の３パターンが考えられます。

１．ダイエットプログラムを行う前後で体重は同じではない。
２．ダイエットプログラムを行う前後で体重は増えている。
３．ダイエットプログラムを行う前後で体重は減っている。

どの対立仮説を用いるかによって、「片側検定」か「両側検定」かが決まってきます。

片側検定

前章の対立仮説の例だと、

２．ダイエットプログラムを行う前後で体重は増えている。
３．ダイエットプログラムを行う前後で体重は減っている。

を立てた時が当てはまります。

仮説検定は正規分布を使うことを基本としているので、端になればなるほど起こりにくい確率と言えます。
（t分布やF分布といったものも出てきますが、ほぼ正規分布のようなもの）

イメージとしては以下の図の通り。
（正規分布が少し左右に歪んで見えますが、左右対称のグラフと考えてください）

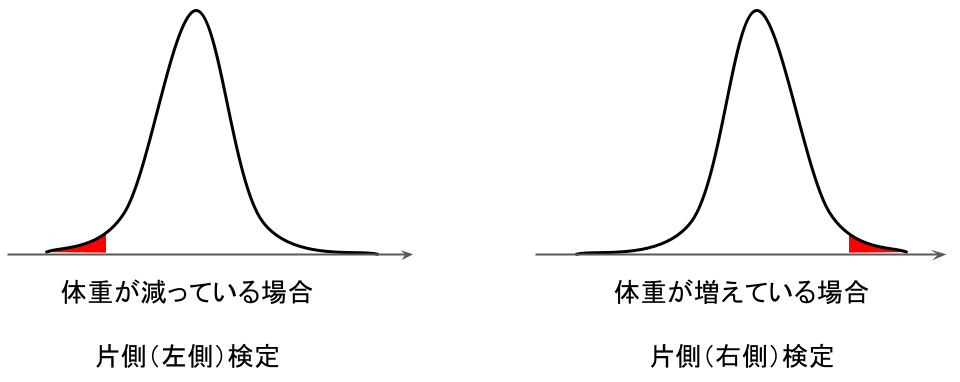
このように
・「確率が高い」ことを示したい場合には、右側の裾の部分
・「確率が低い」ことを示したい場合は、左の裾の部分
を使用します。

今回は「あるダイエットプログラムで体重が変化したかどうかを知りたい」という例でした。

つまり、対立仮説としては「２．ダイエットプログラムを行う前後で体重は減っている」を立てたいですね。

両側検定

前章の対立仮説の例だと、

１．ダイエットプログラムを行う前後で体重は同じではない。

を立てた時が当てはまります。

両側検定も片側検定と同じような、以下のイメージになります。

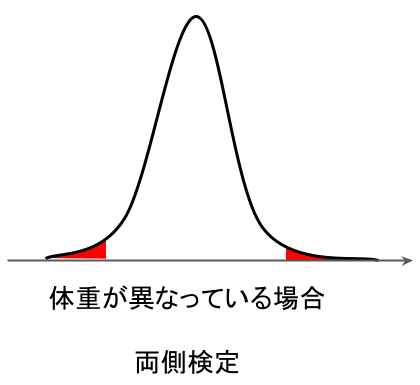
異なる点は、左右両方の裾を考慮する点。

まさに「両側」検定ですね。

もし対立仮説が採用された場合「同じではない」ことが分かるだけで、高い or 低いということは分からないので、注意してください。

DS８０：t検定・z検定などを適切に選択、適用できる

この項目では「2群の平均に差があるかどうか」を知りたい時に用いる検定手法を理解しましょう。

「2群の平均に差があるかどうか」というのは、検定においては一般に広く行われる内容です。

とある事象に効果があったかどうかを調べるために用いるので、差があれば効果があったとなるわけです。

ではまず、使い分ける検定手法の全体像を見ていきましょう。

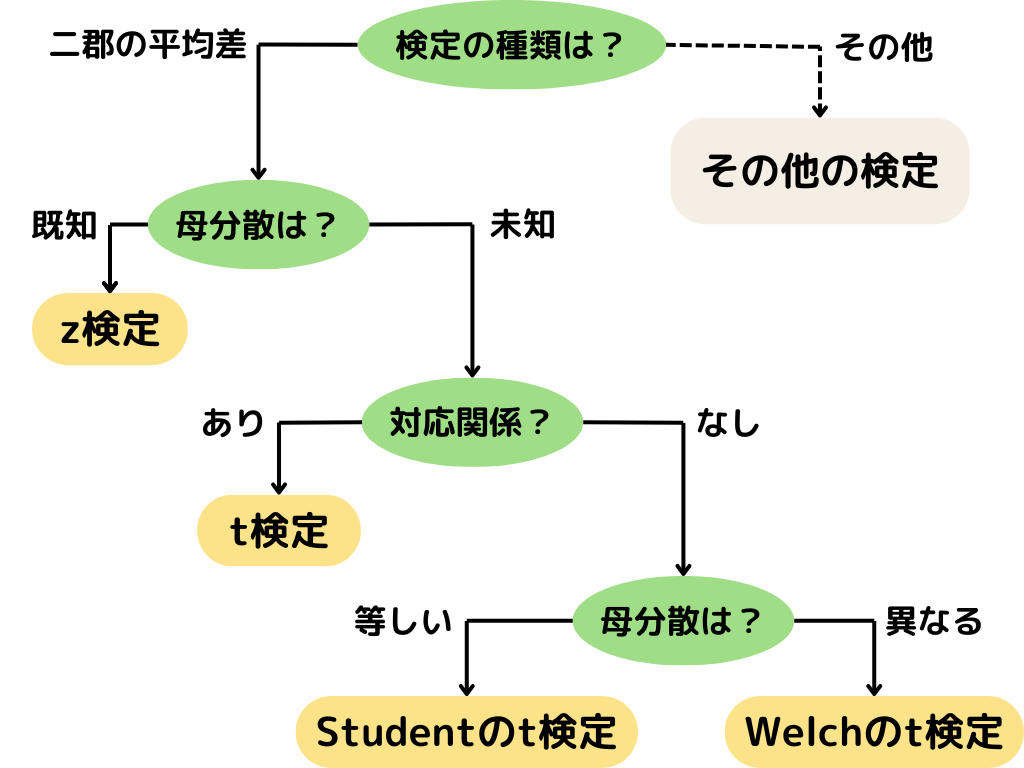
まずは「母分散が既知であるかどうか」でz検定とt検定に分かれます。

z検定

標準正規分布表での検定量\(\displaystyle z_0\)の確認方法は、DS検定の範囲外なので割愛します。

統計検定量\(\displaystyle z\)は以下の式で求められます。

\(\displaystyle z=\frac{\mu-\mu_0}{\frac{\sigma}{\sqrt{n}}}\)

\(\displaystyle \mu\)：サンプルデータ群（標本）の平均値
\(\displaystyle \mu_0\)：基準となるデータ群（母集団）の平均値
\(\displaystyle \sigma\)：基準となるデータ群（母集団）の分散
\(\displaystyle \n\)：サンプル数

しかし実用するとなると「母分散が既知である」ということはほとんどありません。

そのため、母分散が分からなくても使えるt検定を用いるわけです。

t検定

t検定の手法を使い分けるために、「対応のあるデータ」「対応のないデータ」という概念が重要になります。

まずt検定の前提として、二郡の母集団の平均に差があるかどうかを検定する手法でしたね。

この二郡データが「対応のあるデータ」と言えるのは、個々のデータは二郡で同じ場合。

例えば、
・ある学校Aクラスの平均点が、指導方法の変更前後で変わったか
・広告を出す前と出した後で、製品Bの1日の売り上げに変化はあったか　　など

これらは二郡データはありつつ、個々のデータは「Aクラスの生徒の点数」や「製品Bの売り上げ」で同じデータです。（時系列が異なるだけですね）

「対応のあるデータ」を検定する際に用いるのが、t検定。

統計検定量\(\displaystyle t\)は以下の式で求められます。

\(\displaystyle z=\frac{\mu-\mu_0}{\frac{\hat{\sigma}}{\sqrt{n}}}\)

\(\displaystyle \mu\)：サンプルデータ群（標本）の平均値
\(\displaystyle \mu_0\)：基準となるデータ群（母集団）の平均値
\(\displaystyle \hat{\sigma}\)：不偏分散
\(\displaystyle \n\)：サンプル数

統計検定量\(\displaystyle z\)と混同しやすいので、注意してくださいね。

分散に「不偏分散」というものを用いています。

z検定では母集団の分散が分かっていたので、そのまま使用できました。

しかしt検定では母集団の分散が分からないので、代わりに不偏分散を使おうという発想です。

Studentのt検定・Welchのt検定・F検定

逆に二郡データが「対応のないデータ」と言うのは、個々のデータが二郡で異なる場合。

例えば、
・ある学校のAクラスとBクラスの平均点に差があるか
・製品Cと製品Dの1日の売り上げに差はあるか　　など

これらは二郡データの個々のデータが異なりますよね。

Aクラスの生徒とBクラスの生徒は異なりますし、製品Cと製品Dももちろん異なります。

「対応のないデータ」を検定する際に用いるのが、Studentのt検定とWelchのt検定。

ではこの二つはどのように区別するのでしょうか。

一言で言えば「母分散が等しいかどうか」で判断します。

・母分散が等しければ、Studentのt検定
・母分散が等しくなければ、Welchのt検定

母分散が等しいか等しくないかって判断できるの？と思った方もいるでしょう。

もちろん、具体的な一つの値が分かるということはありません。

実は「母分散が等しいか等しくないか」の判断にも、検定が使われるのです。

その検定がF検定。

F検定で母分散が等しいかどうかを調べた後に、Studentのt検定とWelchのt検定のどちらを使うかを決めます。

「Studentのt検定」「Welchのt検定」「F検定」に関しては具体的な式などを覚える必要はありません。

これらの検定で何ができるのかを理解しておくことが、DS検定の合格には重要だと思います。

ここまでで色々出てきて混乱しやすいので、もう一度最初の図を載せておきますね。

まとめ

今回は「片側検定・z検定・t検定」などを解説してきました。

以下の項目を説明できるようになっているでしょうか？

DS検定は覚える内容が多いです。

一つ一つを細部まで見るというよりは、広く浅く見ていくことが重要かと思います。

DS検定を取得して、データサイエンティストやAI関連の仕事への道を開きましょう！

次回は「機械学習」「グルーピング」などについて解説していきます。

ではまた～

DS検定対策｜データサイエンス力｜機械学習・グルーピングを勉強！

データサイエンティスト検定の資格対策！今回は「機械学習・グルーピング」編。機械学習・教師あり学習・教師なし学習・階層クラスター分析・非階層クラスター分析・デンドログラムなどを分かりやすく解説～。参考書・教材代わりに使ってみてください！

rike-kotton.com

2023.07.25