※本記事はアフィリエイト広告を含んでいます

どーも、りけーこっとんです。
DS検定の勉強をしよう!と思ったは良いものの、こんな悩みはありませんか?

DS検定ってどうやって勉強すればいいの?
DS検定の勉強の仕方が分からない…

本で勉強するのは分かるけど、高いなぁ…
無料で単語解説されているサイトとかないかな?

DS検定は、始まったばかりの試験だから、対策法とか分からないよね。
じゃあ、このサイトで出題範囲の内容を押さえていこう~
DS検定の解説をすぐ見たいよ!という方は、以下から最初の解説に飛べます。


今回はスキルチェックリスト
「DS70:ROC曲線、AUCを用いてモデルの精度を評価できる」と
「DS72:RMSEなどの評価指標を理解し、精度を評価できる」を解説していくよ~
本サイトでは超重要項目、重要項目、覚えておきたい項目と表記を分けますので、勉強時の参考にしてみてください。
DS検定って、そもそもどんな資格?という方は以下の記事をご覧くださいね。
試験範囲は以下の二つから出題されます。
・スキルチェックリスト
・数理、データサイエンス、AI(リテラシーレベル)モデルカリキュラム
本内容は以下の書籍を参考に作成しております。
なお、本サイトはDS検定の合格を保証するわけではありませんので、ご了承ください。
では早速、内容に入っていきましょう!
※「DS○○:」項目の文章は独自に短縮して表現しております
DS70:ROC曲線、AUCを用いてモデルの精度を評価できる
ROC曲線もAUCも聞き慣れない単語ですよね。
どちらも分類問題に用いられる指標です。
「陽性・陰性の区別が明確に定まらない分類問題を予測するモデルの性能」を評価できるのがROC曲線とAUC。
それぞれ詳しく見ていきましょう。
ROC曲線・AUC
まず「陽性・陰性の区別が明確に定まらない分類問題を予測するモデル」とは何でしょうか。
例えば以下の図のように「気温」を予測モデルに入力して「アイスを買った or 買わない」を出力するモデルがあったとします。
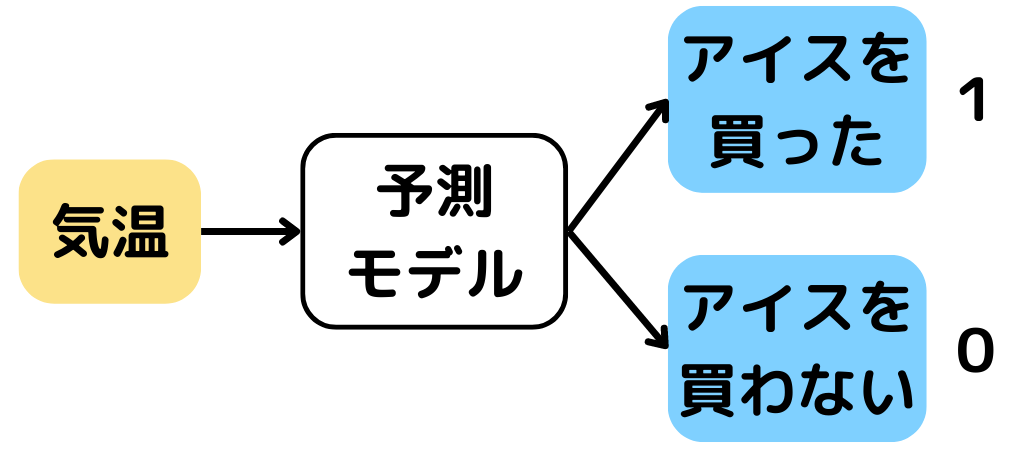
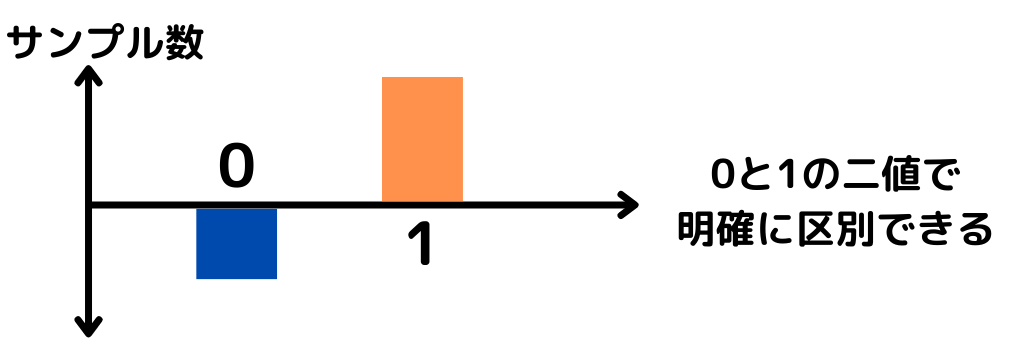
理想は予測モデルの出力が「アイスを買った(1) or 買わない(0)」を明確に出せる数値が存在する以下のような状況。
一般的なロジスティック回帰を用いたとすると、上図の下の例のように出力値が0~1の間で連続値を取るようになるんでしたね。
ロジスティック回帰の予測モデルイメージは以下のとおり。

つまりロジスティック回帰においては、以下の図のように実際のデータが分布すれば理想です。
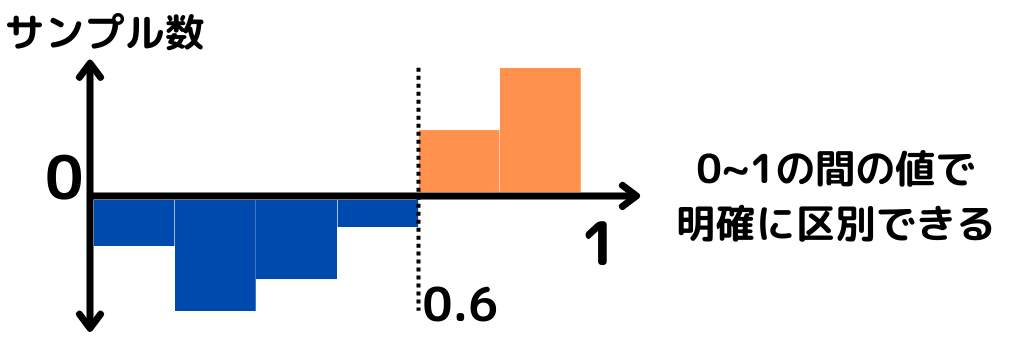
上図の例だと、シグモイド関数の出力値0.6を境にアイスを買った or 買わないが明確に区別できますね。
しかし実データは、同じ気温25℃でもアイスを買う人もいれば、買わない人もいます。
つまり、同じ出力値0.6でも買ったり買われなかったりするわけです。
そうなると、実際のデータ分布は以下のようになることがほとんど。
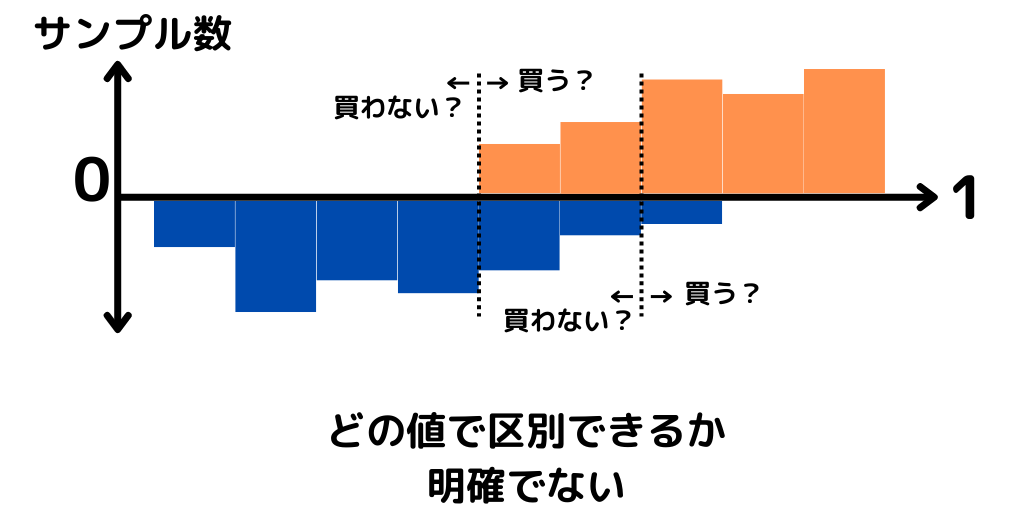
この図になると先ほどよりも、どの気温からは買う傾向にあるのかが判断しにくいですよね。
そこで便利になるのがROC曲線とAUC。
ROC曲線(Receiver Operating Characteristic)
閾値(上記の例だと気温)を変えた時に、予測モデル出力の「偽陽性率」と「真陽性率」を軸にした、以下のようなグラフのこと。
分類問題の精度評価指標。
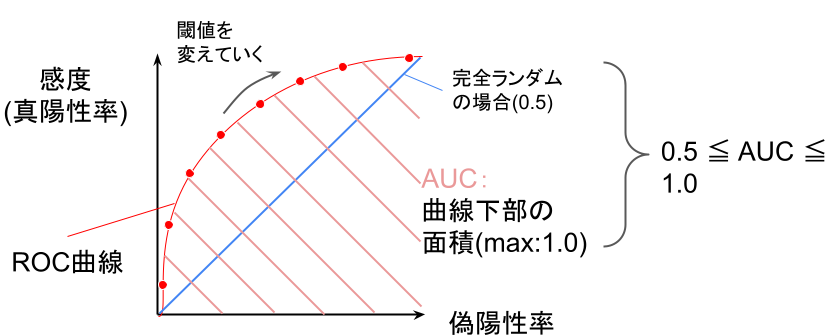
AUC(Area Under the Curve)
上記のグラフで、ROC曲線の下部分を占める面積のこと。AUCの値は0.5以上1.0以下しか取らない。
分類問題の精度評価指標。
グラフの作成手順は以下の通り。
1.閾値(上記の例では気温)を決め真陽性率・偽陽性率を計算
2.横軸:偽陽性率、縦軸:感度(真陽性率)のグラフにプロット
3.閾値を変更する
4.1~3を繰り返す
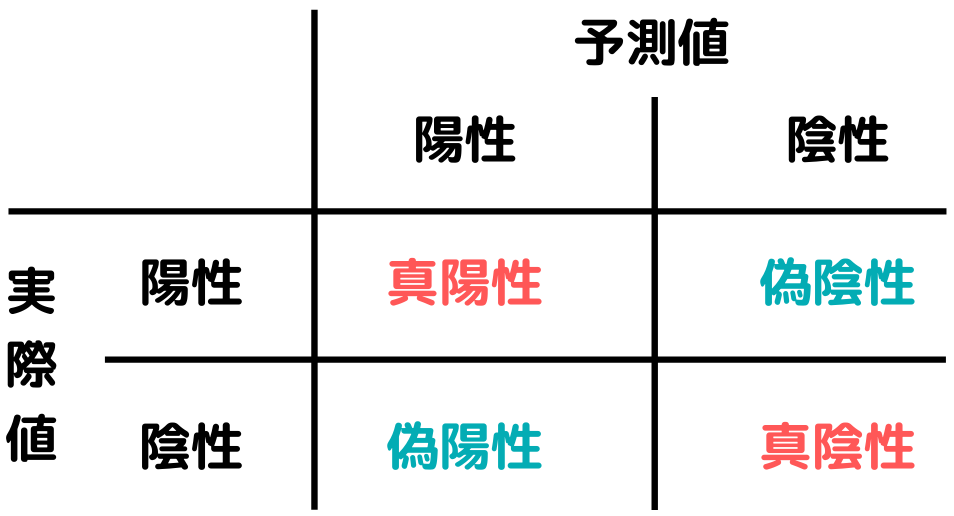
「真陽性率」に関しては、混同行列のところでも出てきていますが、新しく出てきた「偽陽性率」も含めて解説します。
混同行列とは以下のような表を言うのでした。
まずは「真陽性率」の式から。
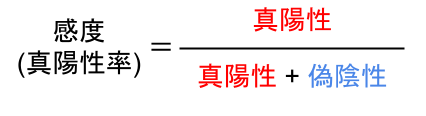
真陽性率は「再現率(Recall)」と同じ式になっています。
意味は「実際に陽性のデータの中で、どれだけ正しく陽性と判断できたか」。
次に「偽陽性率」の式。
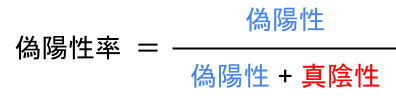
意味は「実際に陰性のデータの中で、どれだけ間違って陽性と判断したか」になります。
DS72:RMSEなどの評価指標を理解し、精度を評価できる
上記で触れたROC曲線や混同行列は、分類問題を予測するモデルの精度評価指標でした。
この章で触れるのは「回帰問題を予測するモデル」の精度評価指標。
代表的なものには以下の4つがあります。
・RMSE
・MAE
・MAPE
・決定係数
それぞれ詳しく見ていきましょう。
RMSE(Root Mean Squared Error)
RMSE(Root Mean Squared Error)
「実際のデータ」と「予測モデルの出力値」の差を計算して、二乗平均にルートを取ったもの。(根平均二乗誤差)
式は以下の通り。
まず(\displaystyle y_i – \hat{y}_i)^2\)の部分で「実際のデータ」と「予測モデルの出力値」の差(残差)を計算しています。
残差の二乗の平均を取り、その値のルートを取ったものがRMSEですね。
機械学習やデータサイエンスの回帰問題では、最も使用される評価指標かもしれません。
RMSEは、実際のデータとの差を取っているため、小さければ小さいほど良いモデルということになります。
「実際のデータ」と「予測モデルの出力値」の差を二乗するため、誤差が大きいデータ程より大きい「罰(誤差)」を与えるイメージでしょうか。
誤差が大きいものをなるべく減らしたい時に、有効な指標ですね。
MAE(Mean Absolute Error)
MAE(Mean Absolute Error)
「実際のデータ」と「予測モデルの出力値」の差の絶対値を計算して、平均を取ったもの。(絶対平均誤差)
式は以下の通り。
RMSEは「実際のデータ」と「予測モデルの出力値」の差を二乗していたため、誤差が大きいものにはより大きな「罰」を与えるイメージでした。
MAEは二乗しないので誤差が大きかろうが小さかろうが、与える「罰」の大きさには関係ありません。
単純に「残差の平均」を見たい時には、RMSEよりMAEの方が良いでしょう。
MAPE
MAPE
「実際のデータ」と「予測モデルの出力値」の差を「実際のデータ」で割った絶対値を計算して、平均を取ったもの。(平均絶対パーセント誤差)
式は以下の通り。
少し複雑ですね。
簡単に言うとMAEの差の計算に「実際のデータで割る」操作を加えただけ。
そうすると実際のデータに対する割合が出るので、平均絶対”パーセント”誤差というわけですね。
パーセントという直感的に分かりやすい指標なので、ビジネスシーンで相手に説明するときなどに使われるようです。
決定係数
決定係数に関しては「DS検定対策|データサイエンス力|回帰分析・最小二乗法・決定係数を勉強」でも触れていますが、もう一度解説します。
決定係数
回帰モデルがどれだけ上手く教師データを説明できているかを測る指標のこと。\(\displaystyle R^2\)で表される
決定係数は1~0の間の値を取り、1に近いほど教師データをよく説明できていると言えます。
「予測の正確さ」を表す指標のため、機械学習の文脈でよく使われますね。
データサイエンスの文脈で、データ分析を行う際に決定係数を扱う際には注意が必要です。
1.アイスの売り上げを「気温」を変数として予測したい
2.アイスの売り上げに「気温」が影響あるかどうかを知りたい
1の場合は問題なく決定係数が使えます。
しかし2の場合に決定係数を用いるのは適切ではありません。
「影響の有無を知りたい」のであって、売り上げを予測したいわけではないからです。
まとめ
今回は「予測モデルの評価」などを解説してきました。
以下の項目を説明できるようになっているでしょうか?
・ROC曲線
・AUC
・RMSE
・MAE
・MAPE
・決定係数
DS検定は覚える内容が多いです。
一つ一つを細部まで見るというよりは、広く浅く見ていくことが重要かと思います。
DS検定を取得して、データサイエンティストやAI関連の仕事への道を開きましょう!
次回は「推定」「検定」などについて解説していきます。
ではまた~

DS検定の続きの解説は以下のページからどうぞ!


![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/214d380e.96fa3830.214d380f.9c4125c0/?me_id=1213310&item_id=20632239&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F8326%2F9784297128326_1_2.jpg%3F_ex%3D240x240&s=240x240&t=picttext)







コメント