※本記事はアフィリエイト広告を含んでいます
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/214d380e.96fa3830.214d380f.9c4125c0/?me_id=1213310&item_id=20632239&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F8326%2F9784297128326_1_2.jpg%3F_ex%3D240x240&s=240x240&t=picttext "[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]")
どーも、りけーこっとんです。
DS検定の勉強をしよう！と思ったは良いものの、こんな悩みはありませんか？
DS検定ってどうやって勉強すればいいの？
DS検定の勉強の仕方が分からない…
本で勉強するのは分かるけど、高いなぁ…
無料で単語解説されているサイトとかないかな？
DS検定は、始まったばかりの試験だから、対策法とか分からないよね。
じゃあ、このサイトで出題範囲の内容を押さえていこう～
DS検定の解説をすぐ見たいよ！という方は、以下から最初の解説に飛べます。
今回はスキルチェックリスト
「DS１２２：外れ値・異常値・欠損値を理解し、適切に対応できる」から
「DS１２８：数値データの特徴量化を行える」を解説していくよ～
本サイトでは超重要項目、重要項目、覚えておきたい項目と表記を分けますので、勉強時の参考にしてみてください。
DS検定って、そもそもどんな資格？という方は以下の記事をご覧くださいね。
試験範囲は以下の二つから出題されます。
・スキルチェックリスト
・数理、データサイエンス、AI（リテラシーレベル）モデルカリキュラム
本内容は以下の書籍を参考に作成しております。
なお、本サイトはDS検定の合格を保証するわけではありませんので、ご了承ください。
では早速、内容に入っていきましょう！
※「DS○○：」項目の文章は独自に短縮して表現しております
DS１２２：外れ値・異常値・欠損値を理解し、適切に対応できる
この項目で求められていることは以下の二つ。
・外れ値、異常値、欠損値を理解すること
・外れ値、異常値、欠損値に対して適切な処理を行えること
この三つはデータ分析をする場合において、悪影響を及ぼします。
つまり、これらを判断できなければ精度が悪かったり、間違った分析をしてしまう可能性があるわけです。
それでは外れ値、異常値、欠損値について詳しく見ていきましょう。
外れ値
外れ値
多数のデータと見比べて、極端に離れた値のこと。
例えば体重を測る際に、一人だけ5 kgの人がいたらおかしいですよね。
このように他のデータから見て明らかに離れている値を外れ値と呼びます。
ではどうやって外れ値を判断すればいいのでしょうか？
最も一般的な方法は、以下の二つがあります。
１．平均から「\(\displaystyle \pm3\sigma\)（標準偏差の3倍）」より離れているかどうかで判断する
２．箱ひげ図と四分位数を用いて判断する
平均から「\(\displaystyle \pm3\sigma\)（標準偏差の3倍）」というのは一般的な指標です。
もしデータが正規分布に従っている場合は、平均から\(\displaystyle \pm3\sigma\)以内に99.7%のデータが収まるという法則があるんです。
つまり平均から\(\displaystyle \pm3\sigma\)以上離れているということは、大半のデータとは離れたデータということになりますね。
２の方法に関しては、\(\displaystyle 第三四分位数+1.5\times四分位範囲\)または\(\displaystyle 第一四分位数-1.5\times四分位範囲\)で求められます。
\(\displaystyle 第三四分位数+1.5\times四分位範囲\)より大きければ外れ値
\(\displaystyle 第一四分位数-1.5\times四分位範囲\)より小さければ外れ値
といった具合に判断していきます。
異常値
異常値
外れ値に含まれる概念。外れ値の中で理由が明確になっているもののこと。
先ほどの例と同じように体重を測る際に、一人だけ5 kgの人がいた場合を考えてみましょう。
外れ値とは「なぜ5 kgになっているのか」という理由までは分からない状態での値のことを言うのでした。
では5 kgになっている理由が「紙に体重を転記する際に小数点の位置を間違えていた」と分かったとしましょう。
すると、この5 kgという値は異常値という呼び方に変わります。
呼び方が変わるんだなぁ、くらいでいいと思います。
また異常値かどうかを判断する方法は「外れ値」と同じです。
外れ値と異常値、混同しやすいので注意しましょう。
欠損値（欠測値、欠落値）
欠損値
データが欠けていて、記録がない・存在していない状態のこと。
データがない理由は様々です。
アンケートが空欄だった、システムの不具合でデータが取れていなかった、などなど…
欠損値の部分は、以下のような対応がとられることが多いです。
・データ分析から外す
・全て同じ値で補完する（例えば0） など
以上で見てきたように、外れ値、異常値、欠損値はデータ分析で悪影響を及ぼします。
データ分析を始める前に、これらの値がないかどうかチェックし、適切に対応することが重要です。
DS１２４：標準化を理解し、適切に行える
ここではデータ加工のうち、標準化という手法を見ていきます。
データ加工の中でも代表的な処理なので、覚えておきたいですね。
標準化
標準化
それぞれのデータから平均値を引き、標準偏差で割るデータの加工方法。加工後のデータを平均0、分散1にする手法。
以下の式で表せる。
\(\displaystyle Z=\frac{X-\mu}{\sigma}\)
\(\displaystyle Z: 標準化後の各データ\)
\(\displaystyle X: 標準化前の各データ\)
\(\displaystyle \mu: 平均\)
\(\displaystyle \sigma: 標準偏差\)
標準化は、データ同士の単位やスケールが異なり、最大値・最小値がない場合や、外れ値が存在する場合に用います。
例えば身長と体重のデータを同時に扱いたいとしましょう。
身長のデータは一般的に140 cm～200 cmくらいの間で数字が推移しますよね。
一方、体重のデータは40 kg～100 kgで推移するでしょう。
このように身長と体重では数字の推移する範囲が違います。
ここで例えば、それぞれの最大値を直接比較すると「身長が200、体重が100だから身長の方が大きい傾向にある」みたいな解釈をしてしまうわけです。
そもそも身長と体重を比較するなんて直感的にも違和感がありますし、適切な解釈ができませんよね。
また、標準化と似た手法として「正規化」というものもあります。
正規化
正規化
それぞれのデータから最小値を引き、データの範囲（\(\displaystyle 最大値-最小値\)）で割るデータの加工方法。加工後のデータを最小値0、最大値1にする手法。
以下の式で表せる。
\(\displaystyle Z=\frac{X-X_{min}}{X_{max}-X_{min}}\)
\(\displaystyle Z: 正規化後の各データ\)
\(\displaystyle X: 正規化前の各データ\)
\(\displaystyle X_{max}: 最大値\)
\(\displaystyle X_{min}: 最小値\)
正規化は、データ同士の単位やスケールが異なり、最大値・最小値が決まっている場合や、標準化よりも計算量を減らしたい場合に用います。
※いろんな分野で「正規化」という言葉があり、分野ごとに意味が異なる場合もあるので注意しましょう。
機械学習やデータサイエンスの文脈では上記の意味で使われやすいです。
一般的には標準化が使われることが多いですが、「正規化」と「標準化」の違いについても理解しておきたいですね。
DS１２５：名義尺度の変数をダミー変数に変換できる
実際のデータは、比例尺度・間隔尺度・名義尺度・順序尺度などがあったことを覚えているでしょうか？
このうち名義尺度はデータに名前やラベルを付けるだけなので、数字ではありません。
名義尺度をAIや機械学習で扱えるようにするのが、ダミー変数です。
ダミー変数
ダミー変数
対象の名義尺度に該当するか否かによって0か1の二値を与える変数。該当すれば1、該当しなければ0を与える。
コンビニでのアイスの売上データを例に見ていきましょう。
例えば以下のデータがあったとします。
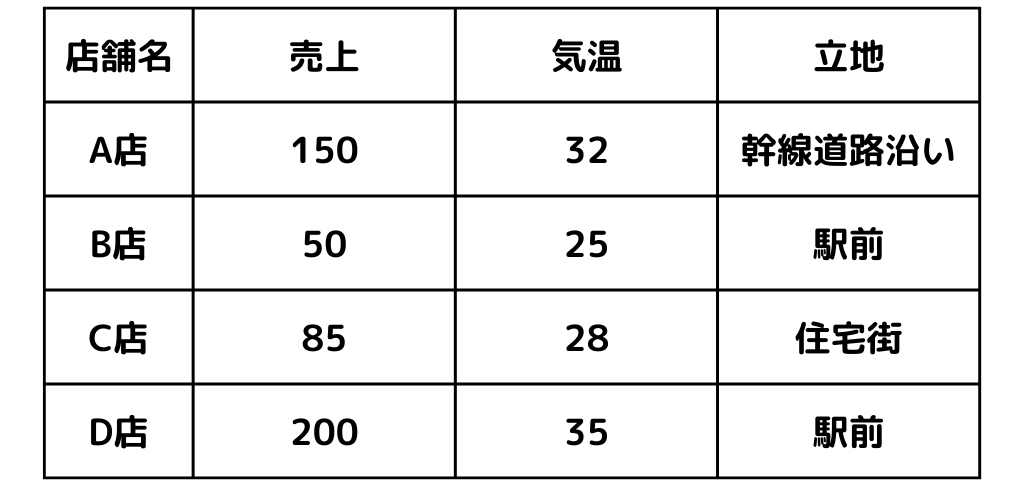
ここで「売上」「気温」は量的変数なので、機械学習でもそのまま扱えます。
しかし「立地」は「幹線道路沿い」「駅前」「住宅街」と名義尺度になっていますね。
そこでデータに新しく列（ダミー変数）を加えます。
以下のようなダミー変数を新たに加えています。
・立地が「駅前」のデータなら1、それ以外なら0
・立地が「住宅街」のデータなら1、それ以外なら0
ここでの注意点は、用意するダミー変数は3つではなく2つということ。
つまり「立地が”幹線道路沿い”のデータなら1、それ以外なら0」という列は必要ありません。
「駅前」と「住宅街」がどちらも0ならば、自動的に「幹線道路沿い」に決まるからですね。
このようにダミー変数は\(\displaystyle 名義尺度の水準数-1\)の数だけ用意します。
「名義尺度の水準数」というのは、上記の例だと3つ（駅前、住宅街、幹線道路沿い）ですね。
DS１２８：数値データの特徴量化を行える
機械学習やAIモデルが高い精度を出すには、入力する特徴量が重要になります。
高精度のモデルを作成するために、元データの特徴を上手く反映した特徴量を作成することを特徴量エンジニアリングと言います。
以下では特徴量エンジニアリングについて、いくつかの手法に触れていきます。
二値化/離散化
二値化/離散化
もともと連続値であったデータを、二値にしたり離散値にする方が特徴を反映できる場合に行う処理。
例えば「体重」のデータを連続値ではなく、〇〇kg台ごとに扱いたい場合があったとしましょう。
この場合、そのまま体重のデータを使うよりも「30 kg以上40 kg未満」「40 kg以上50 kg未満」「50 kg以上60 kg未満」というように分けたいですよね。
すると以下のようにデータを作成しなおすのが適切かもしれません。
「30 kg以上40 kg未満」→ 全て30にする
「40 kg以上50 kg未満」→ 全て40にする
「50 kg以上60 kg未満」→ 全て50にする
このように業務の内容に合わせて利用することが重要です。
対数変換
対数変換
同じ説明変数の中でスケールが大きく異なっており、分布が大きくゆがんでいる場合に用いられる処理。データに対数を取ること。
例えばデータの範囲は0～500なのに、データのほとんどは0～100に収まっている場合に用いられます。
ヒストグラムは以下の通り。
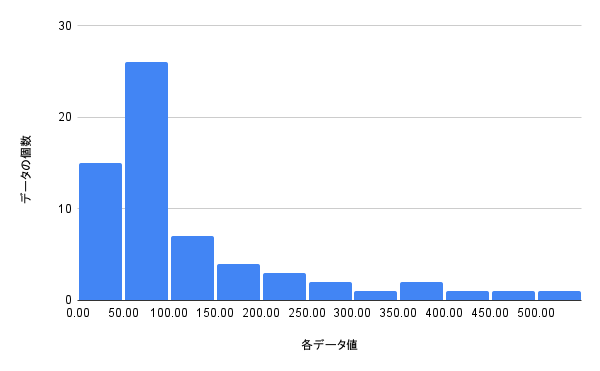
このような分布を「右の裾が長い」「右に歪んだ分布」などと表現します。
データのスケールは大きいのに（0～500）、分布はゆがんで（ほとんどが0～100にある）いますよね。
この分布に対して、全データに対数を取ると以下のようになります。
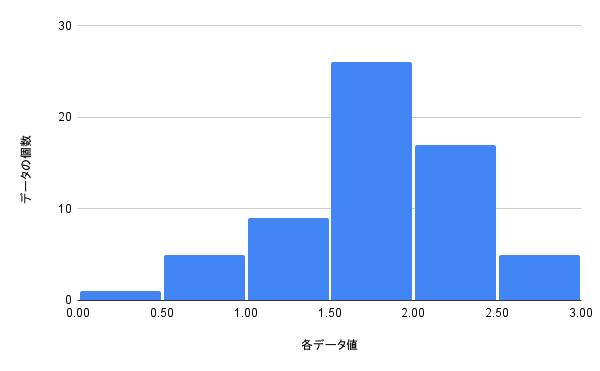
正規分布に近くなりましたね。
また、対数変換を一般化した「Yeo-Johnson変換」や「Box-Cox変換」がありますが、名前だけ覚えておけばDS検定は問題ないと思います。
スケーリング/正規化
スケーリング/正規化
異なる説明変数の間でスケールが大きく異なっており、説明変数同士のスケールの違いを小さくしたい時に行う処理。標準化や正規化がある。
こちらは上述の章「DS１２４：標準化を理解し、適切に行える」でも出てきましたね。
先ほどの対数変換は「同じ説明変数の中で」大きくスケールが異なり、分布が歪んでいる場合に用いられました。
しかしスケーリング/正規化は「異なる説明変数間で」大きくスケールが異なる場合に使用します。
詳しくは上記の標準化や正規化の説明をご覧ください。
交互作用特徴量の作成
交互作用特徴量の作成
説明変数同士に線形的な関係が見えない場合に、複数の特徴量を掛け合わせて新たな特徴量を作るという手法。
先ほどの例であるコンビニでのアイスの売上データを例に見ていきましょう。
この表には既に、名義尺度を変数化したダミー変数が加えられています。
さらに新しい変数、交互作用特徴量の作成をしていきます。
例えば「売上×立地」の変数を作成したとしましょう。（この変換が本当に有効かどうかは状況によります）
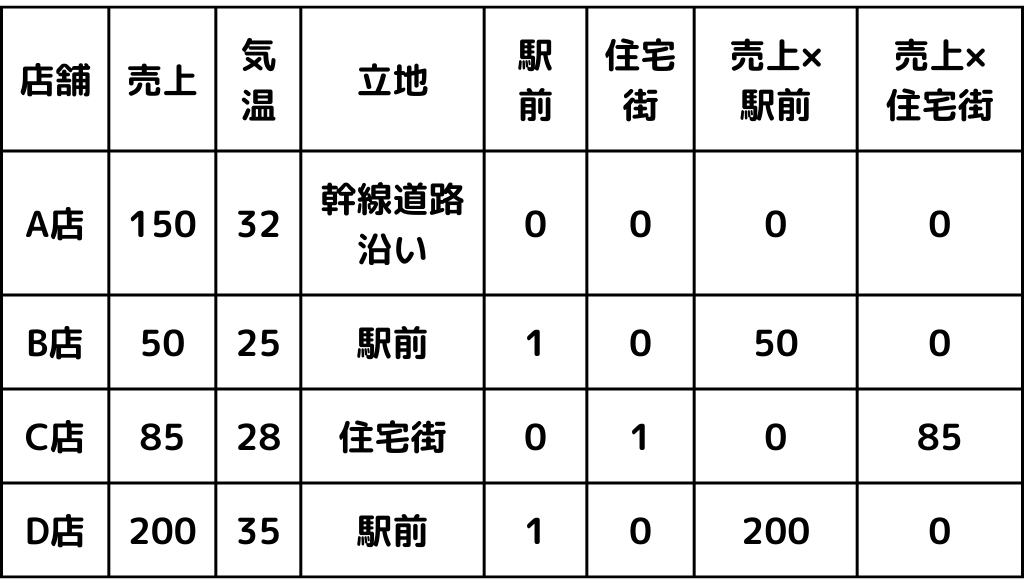
こうすることで、より「駅前」や「住宅街」の店舗だけに絞られた変数の作成が可能です。
ただし、やみくもに変数同士を掛け合わせてしまうことで計算コストが膨大になってしまうので、必要な変数のみに行うことが重要です。
ここまで見てきて分かったと思いますが、全てのデータに共通する特徴量の作成方法はありません。
普段扱うデータをきちんと理解し、どんな特徴が必要かを目的に応じて考えることが重要です。
まとめ
今回は「母平均・標準正規分布・相関と因果」などを解説してきました。
以下の項目を説明できるようになっているでしょうか？
・外れ値
・異常値
・欠損値
・標準化
・正規化
・ダミー変数
・二値化/離散化
・対数変換
・スケーリング/正規化
・交互作用特徴量の作成
DS検定は覚える内容が多いです。
一つ一つを細部まで見るというよりは、広く浅く見ていくことが重要かと思います。
DS検定を取得して、データサイエンティストやAI関連の仕事への道を開きましょう！
次回は「データ可視化」について解説していきます。
ではまた～
DS検定の続きの解説は以下のページからどうぞ！
コメント