※本記事はアフィリエイト広告を含んでいます
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/214d380e.96fa3830.214d380f.9c4125c0/?me_id=1213310&item_id=20632239&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F8326%2F9784297128326_1_2.jpg%3F_ex%3D240x240&s=240x240&t=picttext "[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]")
DS検定の勉強をしよう！と思ったは良いものの、こんな悩みはありませんか？
どーも、りけーこっとんです。
DS検定の勉強をしよう！と思ったは良いものの、こんな悩みはありませんか？
DS検定ってどうやって勉強すればいいの？
DS検定の勉強の仕方が分からない…
本で勉強するのは分かるけど、高いなぁ…
無料で単語解説されているサイトとかないかな？
DS検定は、始まったばかりの試験だから、対策法とか分からないよね。
じゃあ、このサイトで出題範囲の内容を押さえていこう～
DS検定の解説をすぐ見たいよ！という方は、以下から最初の解説に飛べます。
今回はスキルチェックリスト
「DS５３：分析、図表から直接的な意味合いを抽出できる」から
「DS５７：回帰係数、標準偏回帰係数、重相関係数を説明できる」を解説していくよ～
本サイトでは超重要項目、重要項目、覚えておきたい項目と表記を分けますので、勉強時の参考にしてみてください。
DS検定って、そもそもどんな資格？という方は以下の記事をご覧くださいね。
試験範囲は以下の二つから出題されます。
・スキルチェックリスト
・数理、データサイエンス、AI（リテラシーレベル）モデルカリキュラム
本内容は以下の書籍を参考に作成しております。
なお、本サイトはDS検定の合格を保証するわけではありませんので、ご了承ください。
では早速、内容に入っていきましょう！
※「DS○○：」項目の文章は独自に短縮して表現しております
DS５３：分析、図表から直接的な意味合いを抽出できる
データを可視化した際には、その意味合いの抽出が重要です。
理由はグラフを作っただけでは、具体的な行動やビジネスに繋がらないから。
グラフを見て抽出したい意味合いは以下のようなものがあります。
・バラツキ
・有意性
・分布傾向
・特異性
・関連性
・変曲点
・関連度の高低 など
正しい意味合いを抽出するには、前提としてデータが網羅的に集まっていることも条件になります。
具体例を見て、どんなことが言えればいいのか見ていきましょう。
以下は気温の推移を見たグラフになります。
このグラフからの直接的な意味合いの抽出は以下のようなものがあります。
・7月～12月にかけて、最低・平均・最高気温が下がっている
・降水量は7、9月が多い
直接的な意味合いなので、グラフから分かる「事実」を言えればOKでしょう。
ここでは「事実」と「解釈」を混同しないように注意してください。
「解釈」に関しては、後のステップで「何が、なぜ起きているのか」という考察の部分で行います。
DS５４：分析結果の数値を客観的に解釈できる
データ分析の際には、結果の前に仮説を立てます。
仮説通りに分析結果が出れば問題はありません。
しかし、仮説とは大きく異なる分析結果が得られることも多々。
そこで集計ミスをずっと探してしまったり、都合の良いデータを集めたくなってしまいます。
もちろん、都合の良いデータだけを集めるなんてことをしてはいけません。
仮説と異なるデータを受け止めて、得られたデータに対する考察を考えることが重要です。
常にデータを冷静に見極め、データドリブンに結果をとらえましょう。
DS５６：単回帰分析の基本を理解し、モデル構築できる
この項目で挙げられている単回帰分析の基本とは、以下のようなものがあります。
・単回帰分析
・最小二乗法
・回帰係数
・標準誤差
・決定係数
最初に「回帰分析」について触れておきます。
回帰分析とは結果と要因それぞれの変数の関係性を調べること。
別の変数が入力された場合、その変数から導かれる結果を予測もできます。
回帰分析には二種類あり、この項目では「単回帰分析」についての解説です。
単回帰分析
まずは単回帰分析について解説します。
単回帰分析
既存データの「結果」と「要因」が直線の関係性であると仮定して、結果を予測する手法。
説明変数が一つの場合の回帰分析のこと。
\(\displaystyle y=ax+b\)で表されるが、\(\displaystyle x\)の「要因」に当たる変数を説明変数（従属変数）、\(\displaystyle y\)の「結果」に当たる変数を目的変数（独立変数）という。
単回帰分析をイメージ図にすると以下のような感じ。
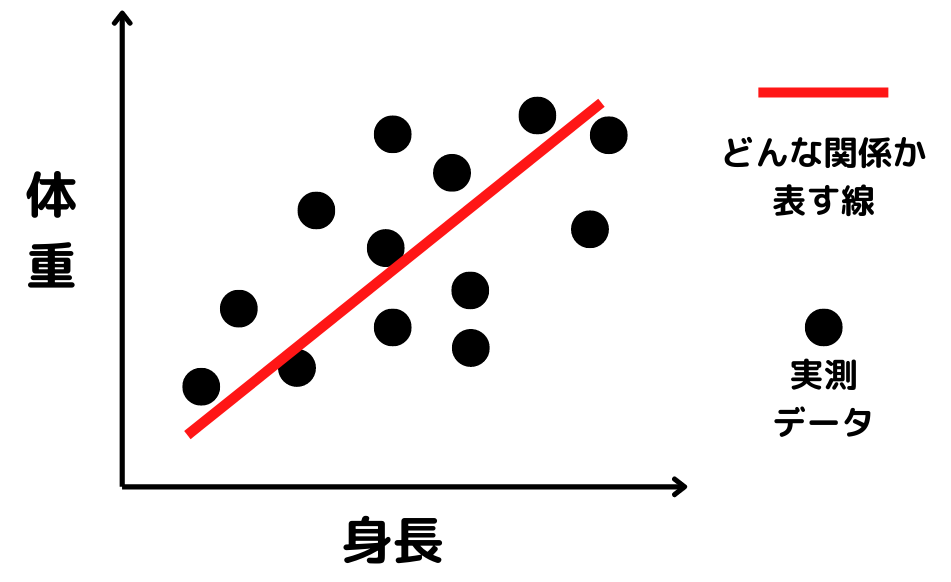
式は\(\displaystyle y=ax+b\)で表されているので、直線です。
\(\displaystyle x\)が身長、\(\displaystyle y\)が体重と考えると、赤い線のような直線関係として結果を予測するのが単回帰分析ですね。
最小二乗法・回帰係数
回帰分析の際に、既存のデータに最も当てはまりそうな関数を探す手法を「最小二乗法」といいます。
最小二乗法
データとの誤差（残差二乗和）を最小にするような関数を探す手法。
残差二乗和のイメージとしては、以下の通り。
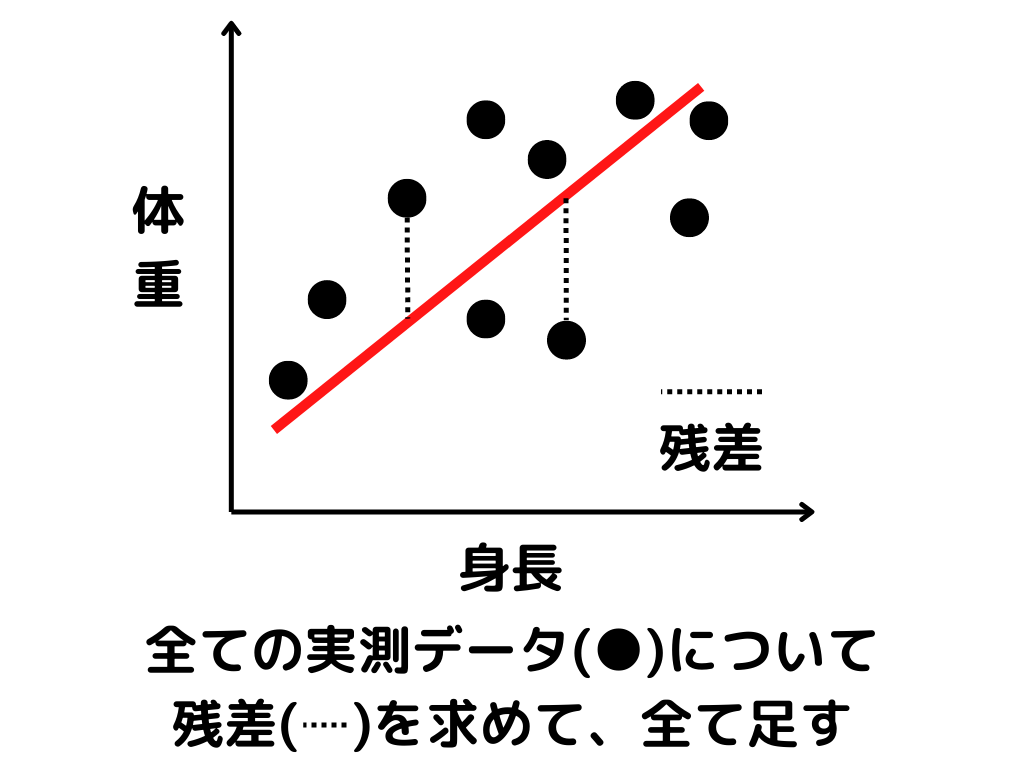
全てのデータと直線の誤差が小さければ、データをよく表している直線ということになりますね。
さて、単回帰分析は直線関係（\(\displaystyle y=ax+b\)）を仮定していました。
この\(\displaystyle a\)と\(\displaystyle b\)には「回帰係数」という名前がついています。
回帰係数
単回帰分析で得られた直線関係の「傾き」と「切片」のこと。
\(\displaystyle y=ax+b\)の\(\displaystyle a\)と\(\displaystyle b\)と同義。
回帰係数の計算方法も軽く触れておきます。
１．変数\(\displaystyle x\)と\(\displaystyle y\)の平均値（\(\displaystyle \bar{x}, \bar{y}\)）を計算
２．それぞれの変数の偏差（\(\displaystyle (x_i-\bar{x}), (y_i-\bar{y})\)）をデータごとに計算
３．変数\(\displaystyle x\)の分散（\(\displaystyle s_{x}^2\)）を求める
４．共分散\(\displaystyle s_{xy}\)を計算する
５．傾き\(\displaystyle a=\frac{s_{xy}}{s_{x}^2}\)を求める
６．切片\(\displaystyle b=\bar{y}-a\bar{x}\)を求める
標準誤差
回帰係数とは、あくまで得られているデータ（標本）を表せる係数のこと。
真のデータ集団（母集団）の回帰係数は分かりません。
すると回帰係数を評価したくなりますよね。
そこで便利なのが標準誤差という指標。
標準誤差
標本平均の値が母平均に対してどれだけバラついているかの指標のこと。
回帰係数のバラつきを表す指標としても用いられる。
\(\displaystyle \sigma_x：標準誤差\)
\(\displaystyle \sigma^2：母集団との標準偏差\)
\(\displaystyle n：標本のサンプルサイズ\)
\(\displaystyle \sigma_x=\sqrt{\frac{\sigma^2}{n}}\)
標準誤差が大きいということは、標本を取るごとに真の回帰係数から離れた値を取ることになります。
つまり信頼性が低い回帰係数ということになるわけですね。
決定係数
標準誤差では「回帰係数a, b」を評価しました。
しかし予測したモデル\(\displaystyle y=ax+b\)を評価したいですよね。
そこで便利なのが決定係数。
決定係数
単回帰モデルがどれだけ上手くデータを説明できているかを測る指標。\(\displaystyle R^2\)で表される。
回帰モデルの精度を評価するとなったら、基本的に決定係数を使うようですね。
DS５７：偏回帰係数、標準偏回帰係数、重相関係数を説明できる
DS５６では「単回帰分析」について触れました。
この項目ではもう一種類の回帰分析である「重回帰分析」についての項目。
重回帰分析の基本について学んでいきましょう。
重回帰分析
重回帰分析
既存データの「結果」と「要因」が直線の関係性であると仮定して、結果を予測する手法。
説明変数が複数の場合の回帰分析のこと。
\(\displaystyle y=a_1x_1+a_2x_2+a_3x_3+\cdots+b\)
簡単に言ってしまえば、単回帰分析の変数\(\displaystyle x\)が複数になっただけですね。
予測式も線形ではなく、曲線などの非線形性になります。
偏回帰係数
偏回帰係数
重回帰分析で得られる\(\displaystyle y=a_1x_1+a_2x_2+a_3x_3+b\)の\(\displaystyle a_1, a_2, a_3\)と\(\displaystyle b\)のこと。
偏回帰係数も、単回帰分析と比較すると覚えやすいです。
基本的には回帰分析の傾き\(\displaystyle a\)に当たる部分が複数になっただけですね。
標準偏回帰係数
標準偏回帰係数
偏回帰係数を平均０、標準偏差１になるように標準化したもの。
重回帰分析には、様々な変数が考慮されます。
例えばアイスクリームの売り上げを目的変数とした場合に、説明変数が「気温」「広告費」「（宣伝のための）ツイート数」みたいなものがあったとします。
この時に、「気温」「広告費」「ツイート数」を数字だけで見ると、スケールが全然違うことが分かるでしょうか。
・気温 ⇒ 20 ~ 35（℃）
・広告費 ⇒ 1000000 ~ 100000000（円）
・ツイート数 ⇒ 1 ~ 100（個）
これらを標準化しないまま分析すると、ほとんど数字の大きい広告費しか考慮されない分析になってしまいます。
広告費の数字に比べれば20や100は微々たるものですからね。
こうならないために、標準偏回帰係数を使用することが基本になります。
重相関係数
０に近いほど分析の精度が悪く、１に近いほど精度が高いことが分かります。
まとめ
今回は「データの洞察・回帰分析」などを解説してきました。
以下の項目を説明できるようになっているでしょうか？
・単回帰分析
・最小二乗法
・回帰係数
・標準誤差
・決定係数
・重回帰分析
・偏回帰係数
・標準偏回帰係数
・重相関係数
DS検定は覚える内容が多いです。
一つ一つを細部まで見るというよりは、広く浅く見ていくことが重要かと思います。
DS検定を取得して、データサイエンティストやAI関連の仕事への道を開きましょう！
次回は「データの予測・評価」などについて解説していきます。
ではまた～
DS検定の続きの解説は以下のページからどうぞ！
コメント