※本記事はアフィリエイト広告を含んでいます

どーも、りけーこっとんです。
「G検定取得してみたい!」「G検定の勉強始めた!」
このような、本格的にデータサイエンティストを目指そうとしている方はいないでしょうか?
また、こんな方はいませんか?
「なるべく費用をかけずにG検定取得したい」「G検定の内容について網羅的にまとまってるサイトが見たい」
今回はG検定の勉強をし始めた方、なるべく費用をかけたくない方にピッタリの内容。
りけーこっとんがG検定を勉強していく中で、新たに学んだ単語、内容をこの記事を通じてシェアしていこうと思います。
結構、文章量・知識量共に多くなっていくことが予想されます。
そこで、超重要項目と重要項目、覚えておきたい項目という形で表記の仕方を変えていきたいと思いますね。
早速G検定の中身について知りたいよ!という方は以下からどうぞ。

具体的にどうやって勉強したらいいの?
G検定ってどんな資格?
そんな方は以下の記事を参考にしてみてください。
なお、りけーこっとんは公式のシラバスを参考に勉強を進めています。
そこで主な勉強法としては
分からない単語出現 ⇒ web検索や参考書を通じて理解 ⇒ 暗記する
この流れです。
※この記事は合格を保証するものではありません
大項目「機械学習の具体的な手法」
G検定のシラバスを見てみると、試験内容が「大項目」「中項目」「学習項目」「詳細キーワード」と別れています。
本記事は「大項目」の「機械学習の具体的な手法」の内容。
その中でも「教師なし学習」というところに焦点を当ててキーワードを解説していきます。
G検定の大項目には以下の8つがあります。
・人工知能とは
・人工知能をめぐる動向
・人工知能分野の問題
・機械学習の具体的な手法
・ディープラーニングの概要
・ディープラーニングの手法
・ディープラーニングの社会実装に向けて
・数理統計
とくに太字にした「機械学習とディープラーニングの手法」が多めに出るようです。
本記事の範囲は、合格に向けては必須の基礎知識になります。
これから先の機械学習の理解を深めるために、そしてG検定合格するために、しっかり押さえておきましょう。
教師なし学習に関する内容が多くなってしまったので、記事を複数回に分割してお届けしようと思いますね。
教師なし学習の概要
教師なし学習とは、どういう特徴や傾向があるか分からないデータに傾向を見出したり、似たデータをまとめたりする機械学習の手法。
教師あり学習とは異なり、その名の通り「教師データ」がありません。
なので、教師なし学習で得られた結果を解釈することは、分析者などの人間が行います。
教師あり学習と教師なし学習の違いは以下の画像の通り。
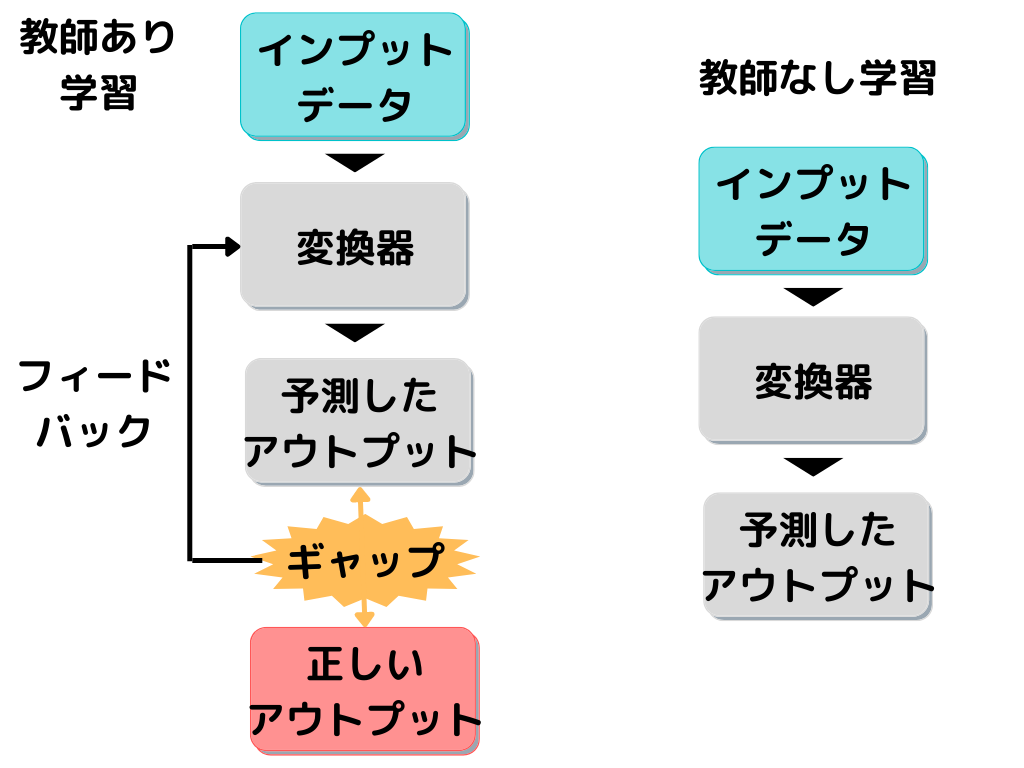
「正しいアウトプット」がないので、教師データがない、つまり「教師なし学習」というわけです。
さらに教師なし学習のイメージはこんな感じ。
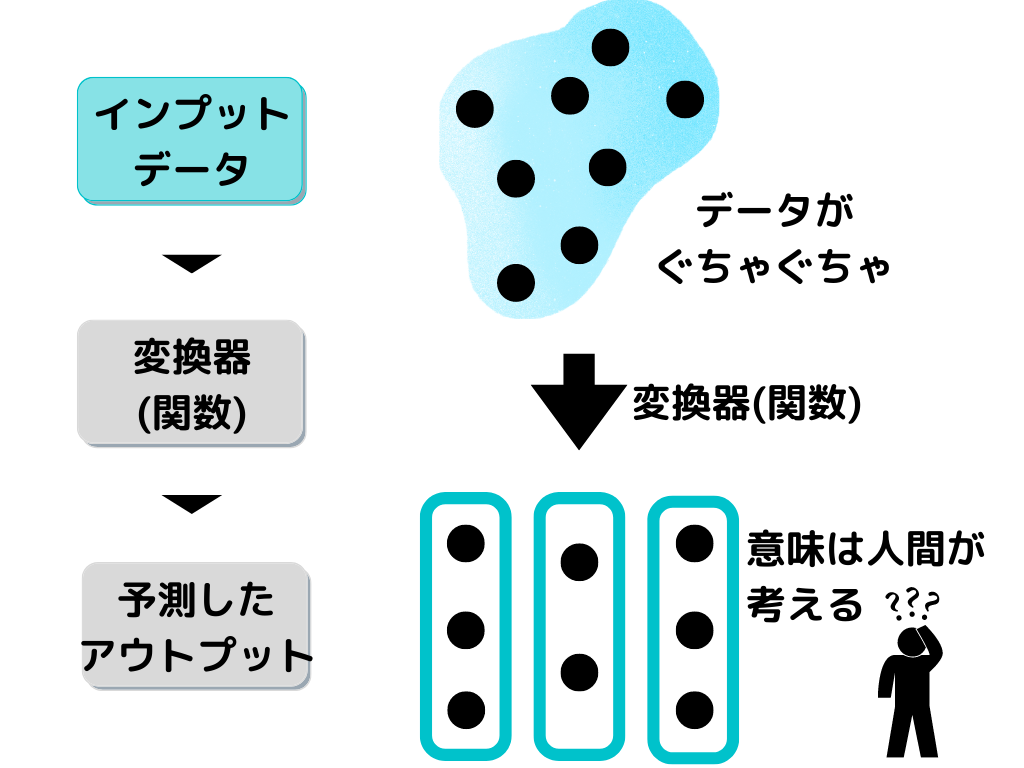
図のように、元々のデータには規則性がなく、ぐちゃぐちゃの状態です。
そのデータに「教師なし学習」を行うことで、どういう規則性があるのか、パターンを見出します。
「教師なし学習」が見つけるのは「パターン化に必要だった関数(変換器)」です。
元データから見出したパターンの解釈を、機械はできません。
規則的にデータをパターン化したら、そこから先は人間の仕事。
規則性から何が言えるのかを考察することで、ビジネスに活かすことができますよね。
今回は教師なし学習の得意とすることの1つ「次元削減・圧縮」の分野に絞って解説していきたいと思います。
次元削減・圧縮
次元削減・圧縮とは、より少ないデータで元のデータを表現しようとすること。
自然言語処理分野などに用いられますね。
「教師なし学習」が得意とすることの1つです。
具体的な手法は以下の通り。
・主成分分析
・非負値行列分解
・潜在的ディリクレ配分法
・特異値分析
・t-SNE
・多次元尺度構成法
非負値行列分解は、シラバスには載っていませんが、重要な手法なので解説に入れています。
実際の現場でも元データが多すぎると、計算に時間がかかってしまいますよね。
そこでデータの特徴をなるべく消さないように、データ量を少なくする方法がいろいろ考えられました。
それでは一つずつ見ていきましょう。

主成分分析
主成分分析とは、複数の変数を計算して一つの軸にまとめる手法。
イメージだと以下の図のような感じです。
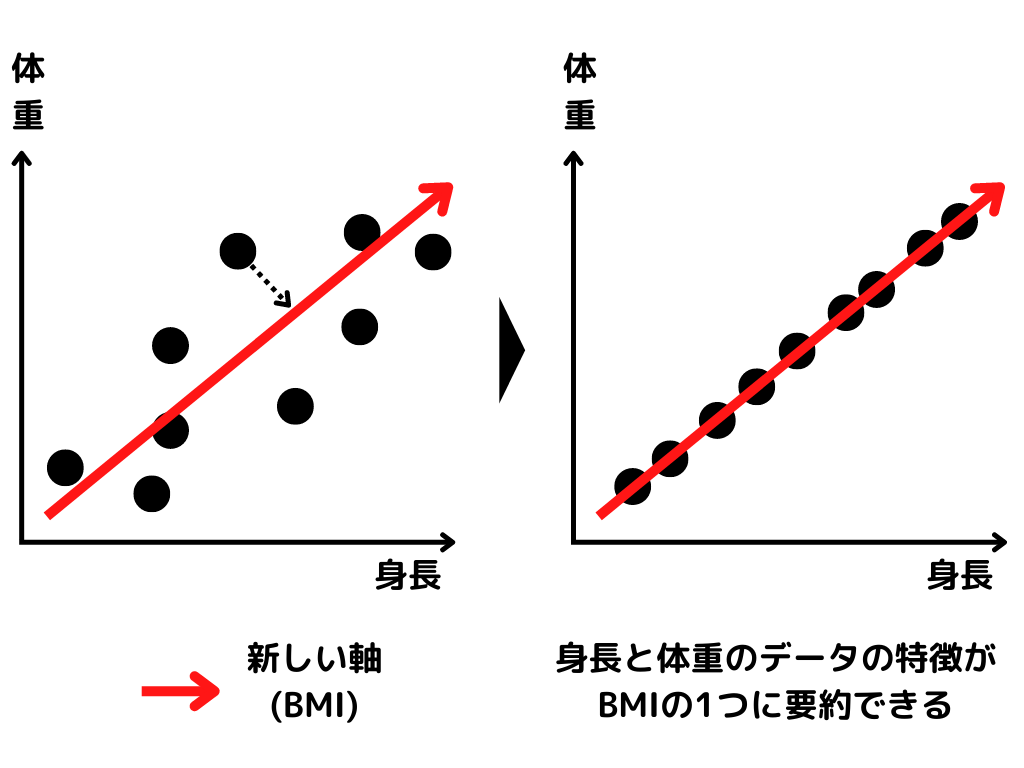
このように2軸あったデータに、新しい軸を1本追加します。
この新しい軸一本に情報を集約することで、2変数のデータから1変数のデータに変わっていまよね。
これが主成分分析です。
分かりやすい例でいうと、BMIがありますね。
これは体重、身長をBMIという一つの軸にしています。
この時、目的関数は「分散が最大になるような軸の式」です。
「分散が最大になるような」を取る理由としては、情報量をなるべく消さないためですね。
使いどころ
主成分分析の使いどころとしては以下のようなものがあるかと。
・顧客満足度調査
・複数ブランドのイメージマップ作成
・特徴量間の相関関係をビジュアルで理解したいとき
非負値行列分解
非負値行列分解とは、ある非負値行列を二つの非負値行列に分解すること
非負値行列とは、全成分が0以上の行列のこと。
つまり非負値行列分解とは、一つの0以上しかない行列を、二つの0以上しかない行列に分けるという事ですね。
情報量が多すぎる一つの行列Aから、掛けることで行列Aを近似できる二つの行列を求めます。
そうすることで、データが少なくなった二つの行列に分けられますよね。
ここの詳しい理解は、シラバスにも載っていないので、「そういうもんなのか」ぐらいでいいと思います。
もちろん理解できる方は、「行列・線形代数」の知識があればできると思いますので、理解してみてください。
使いどころ
使いどころとしては以下の通り。
・自然言語処理で計算効率を上げる
・画像の特徴抽出
まさに現在、流行中の分野に適用されていることが分かりますね。
潜在的ディリクレ配分法(LDA)
潜在的ディリクレ配分法(LDA)とは、A×Bの行列を新たにCの要素を入れてA×CとB×Cの二つに分解すること。
新たなCの要素が、自然言語処理だと「トピック」といわれることもありますね。
元の文章群から、どの単語が出現しやすいのか知りたいときなどに使うようです。
潜在的ディリクレ配分法では、以下に示すような三角のグラフが取得可能。
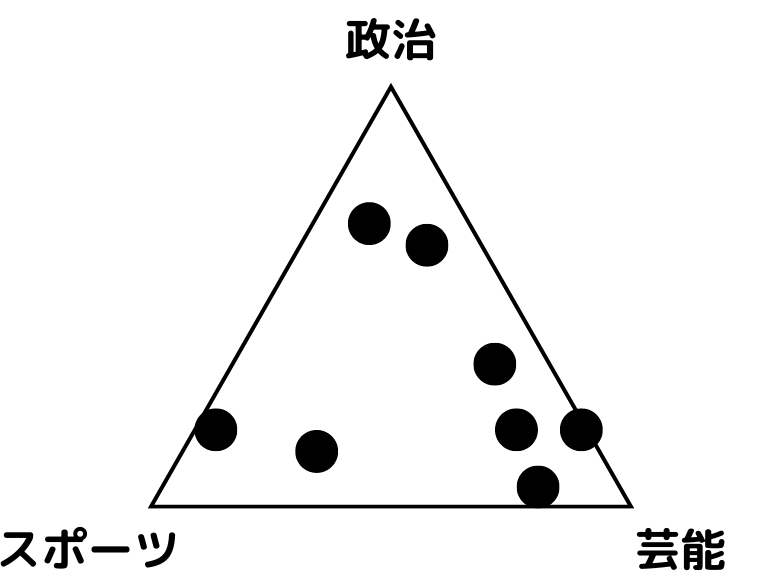
各頂点にある単語が「トピック」ですね。
「トピック」は実際に文書に出てきた単語で構成されています。
ex) 「政治」→内閣、選挙、衆議院…
「スポーツ」→サッカー、野球、NBA…
このグラフは文書内にどの単語が出てきやすいかという、トピックの分布になっています。
三角形の端に行くほど、その文書(●)は、明確に分類できるようですね。
上図だと「政治」「芸能」「スポーツ」の頂点に近いほど、文書(●)は近いトピックの分類という読み解きになるようです。
使いどころ
使いどころは以下の通り。
・自然言語処理のトピック分類、抽出、文書分類
・クラスタリングの代わりとしてユーザーのプロファイリング
特異値分解(SVD)
特異値分析とは、行列に対する行列分解の1手法。
Singular value decompositionの略でSVDと言われることもあります。
潜在的ディリクレ配分法と、行列を分解するという意味では似てますよね。
特異値分解は以下のような感じに行列を分解します。
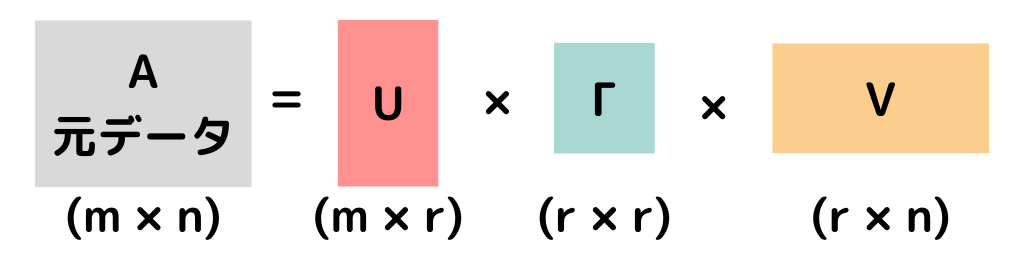
元の行列(A)を、特異値(Γ)・左特異ベクトル(U)・右特異ベクトル(V)に分ける
ということを行っているようですが、専門用語が多いので「そんなもんなのね」でG検定は良いと思います。
特異値分解を行うことで
・行列の特徴(特異値Γで分かる)が見えやすくなる。
・固有値(特異値Γ)を無視して(次元削減)、高精度で近似計算できる。
→近似することで、計算コストが下げられたり、データ量が減らせる。
といったメリットがあるようです。
t-SNE
t-SNEとは、高次元データを二次元や三次元などに圧縮する次元削減の手法。
他の次元削減の特徴と異なるのは以下の点。
・データの局所的な構造(類似したデータを低次元でも近くに保つこと)の維持ができる
・高次元の非線形データも、なるべく圧縮したときに近くに保つ
近くに保つために、距離の分布を用いるのですが、この分布はスチューデンのt-分布を用いています。
t-SNEのtは、t分布のtですね。(t-分布とは何か?までは知らなくても大丈夫だと思います。気になる方はこちら)
多次元尺度構成法(MDS)
多次元尺度構成法とは多変量解析の1手法(主成分分析の仲間)。
Multi-dimensional scalingの略でMDSと言われることもあります。
この手法も、多くのデータをより少ないデータで表す次元削減・圧縮の1手法ですね
分類対象物の関係を、二次元や三次元における点の布置で表現する手法(似た物は近くに、違うものは遠くに配置する)。
作成できるグラフは以下のようなもの。
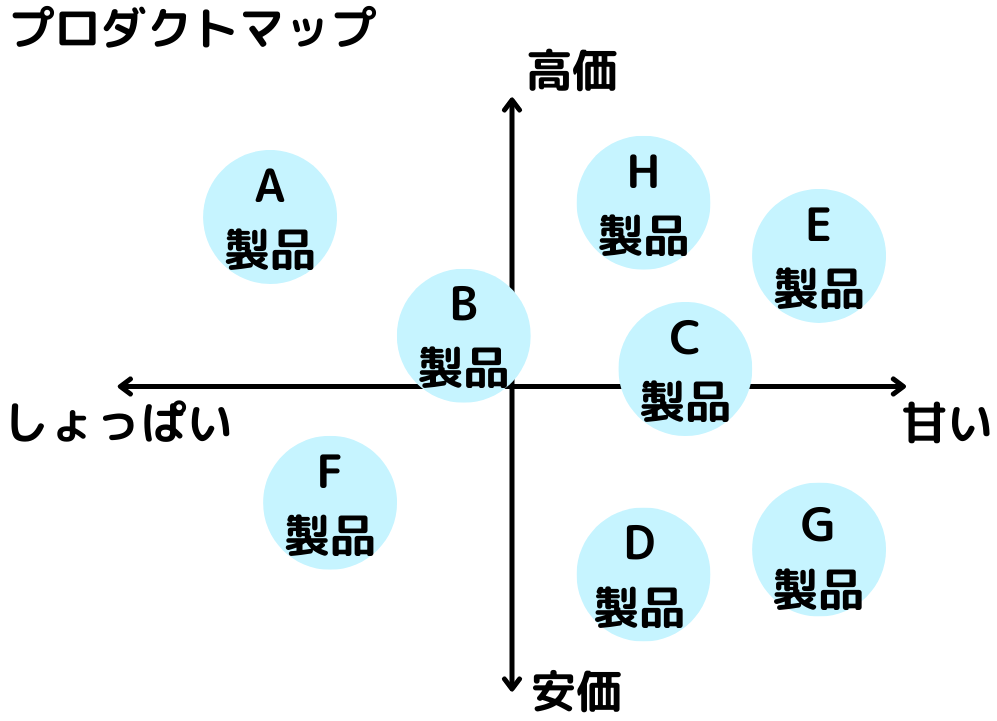
プロダクトマップで、自社製品と他社製品を比べるなど、マーケティング分野との相性が良いようです。
まとめ
今回は大項目「機械学習の具体的手法」の中の一つ教師なし学習についての解説でした。
本記事の覚えておきたいキーワードは以下。
・主成分分析
・潜在的ディリクレ配分法
・特異値分析
・t-SNE
・多次元尺度構成法
以上が大項目「機械学習の具体的手法」の中の一つ教師なし学習の「次元削減・圧縮」の内容でした。
次回は教師なし学習の中でも、代表的な手法「クラスタリング」やそのほかの手法について触れていきたいと思います。
教師あり学習に続き、「教師なし学習」も出題数は多いことが予想されます。
しっかり押さえて、合格目指しましょう!
覚える内容が多いですが、りけーこっとんも頑張ります!一緒に頑張っていきましょう!
ではまた~

続きは以下のページからどうぞ!










コメント