※本記事はアフィリエイト広告を含んでいます

どーも、りけーこっとんです。
皆さんは日々積み重ねていること、地道な努力を頑張っていることはありますか?
りけーこっとんは統計学の基礎だけでも固めておこうかな、と思ってます。
そこで今回は「データ分析のための統計学入門」のまとめの第四弾!
第四章の内容を分かりやすくまとめてみたいと思います。
「このままでは、入社前に全部終わらせるのは無理じゃね?」と思っているところです。
しかし全てを終わらせられなくても、引き続き地道にやって行ければなと。
第一弾はこちら。
それに引き続き、第二弾はこちら
第三弾はこちら
「データ分析のための統計学入門」 とはアメリカのデータサイエンティストの方々が統計について、統計をどう実際の分析や現場に利用していくかを執筆したもの。
「アメリカの人が書いたって事は、英語…?読める気がしない…」
という方も日本語訳があるので大丈夫!(日本語無料版には、練習問題の解説が付いていません)
これから統計を学ぶ人たち、データサイエンティストを目指す人たちは、読んでおいて損はないと思います。
日本統計協会も「大学で初めて統計学を学ぶ学生、ビジネスでデータ分析をしている社会人のために
書かれた豊富で実践的な練習問題を含む最適な統計学入門書」というお墨付き。
何よりも魅力的なのは、無料公開という点!
統計学についてド素人な自分にとって、どの書籍を買ったら良いか分からなかったので、すごくありがたいです。
下のURLから、無料公開されているページに飛べます。
http://www.kunitomo-lab.sakura.ne.jp/2021-3-3Open(S).pdf
今回の記事は「読む前にさらっと概要を知りたい」という人向け。
より厳密な内容、詳しい内容は原文を読んで貰いたいと思うので、ここでは概略を絵を使ってさらっていきたいと思います。
では早速始めていきましょう。
第四章のまとめ
まず、りけーこっとんがこの章で学んだことは以下の3つ。
・確率変数には分布の仕方が数種類ある
・確率変数の分布の形 「正規分布」
・確率変数の分布の形 「二項分布」
「確率変数って何だっけ?」と思った方はこちら。
この記事で復習してから、今回を読むとより分かりやすいと思います。
簡単にまとめると確率変数とは「確率の中でも結果によって変わる確率」のこと。
どの結果かによって確率が変わるので、それは分布を持ちます。
この分布の仕方(分布の形)が、有名な物で数種類あるということですね。
図で簡単に言うとこんな感じ。
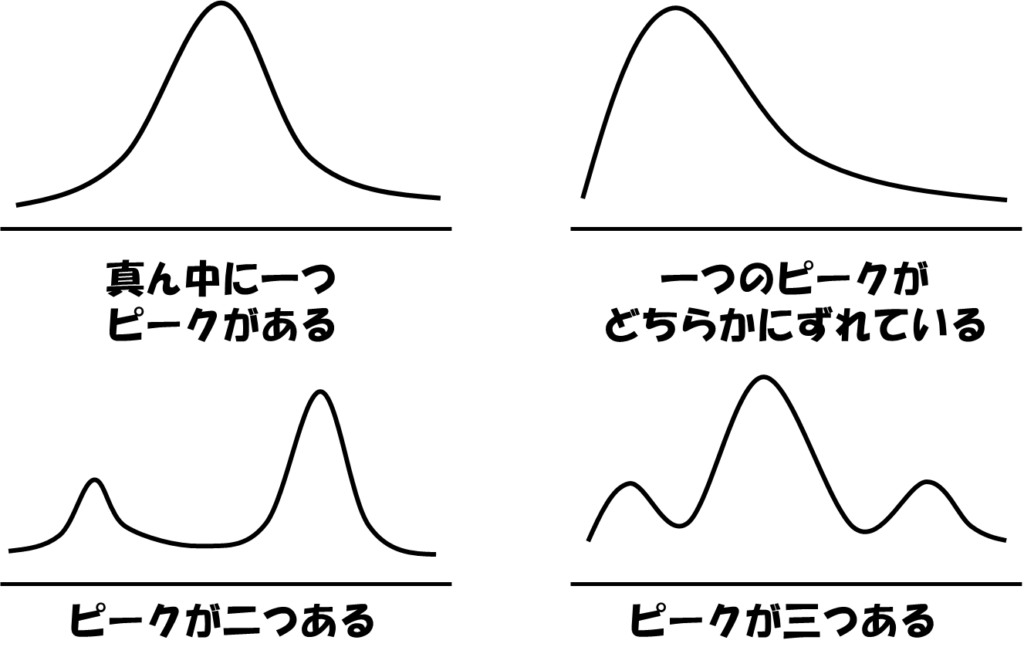
「こんな感じで分布の形が変わるので、有名どころの形は知っておこうぜ」的な感じなのが本章です。
では実際にどんな分布の仕方があるのか見ていきましょう。

確率変数には分布の仕方が数種類ある
確率変数の分布には色んなものがあるというのは、先ほどの章でいったとおりですね。
その中でも、今回本書で挙げられている分布は、以下の5つ。
・正規分布
・幾何分布
・二項分布
・負の二項分布
・ポアソン分布
今回は、初心者からデータサイエンティストや統計学をやろうと思っている人のためにこの記事を書いています。
なので、この5つの中でも基本だと思った”正規分布”と”二項分布”について詳しく取り上げたいと思います。
残りの”幾何分布””負の二項分布””ポアソン分布”は、応用編だったり、本書でも触れる機会が少ない物のようですね。
もし、残りの3つについても知りたい方がいれば、本書を読んでみてください。
確率変数の分布の形 「正規分布」
一番最初に取り上げるのは正規分布。
正直この分布が、実践で一番よく見られる形のようですね。
あまりにもよく見るので、正規曲線・正規分布・ガウス分布という名前で良く出てきます。
正規分布の特徴としては以下の通り。
・常に左右対称
・単峰
・釣り鐘型
・平均と標準偏差が形を決める上で重要
最初の3つの特徴を図で示すと以下の通り。
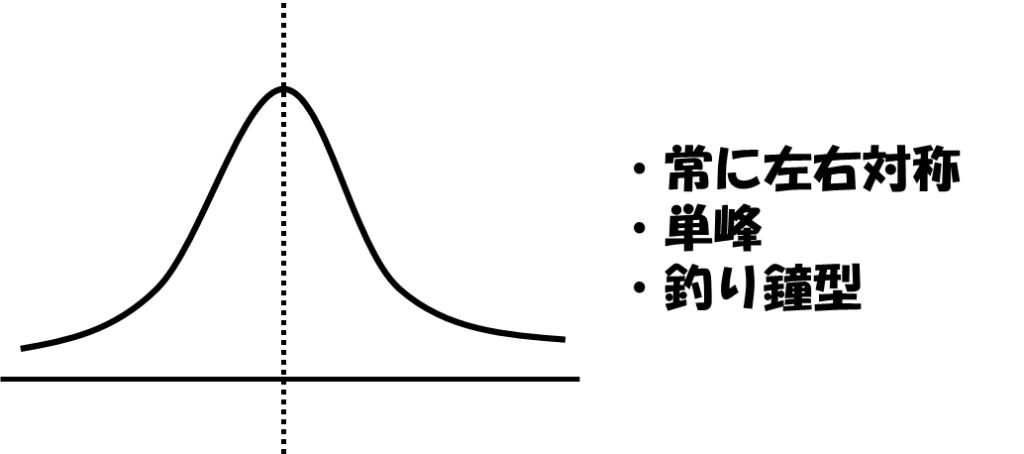
4つ目の特徴が少し難しいですよね。
正規分布で、釣り鐘の中心が平均、釣り鐘の横への広がりが標準偏差を表しています。
つまり、平均が変わると正規分布の位置自体が左右に移動することになりますよね。
標準偏差が変わると、釣り鐘の横への広がりが変わることになります。
これらを図にすると次の通り。
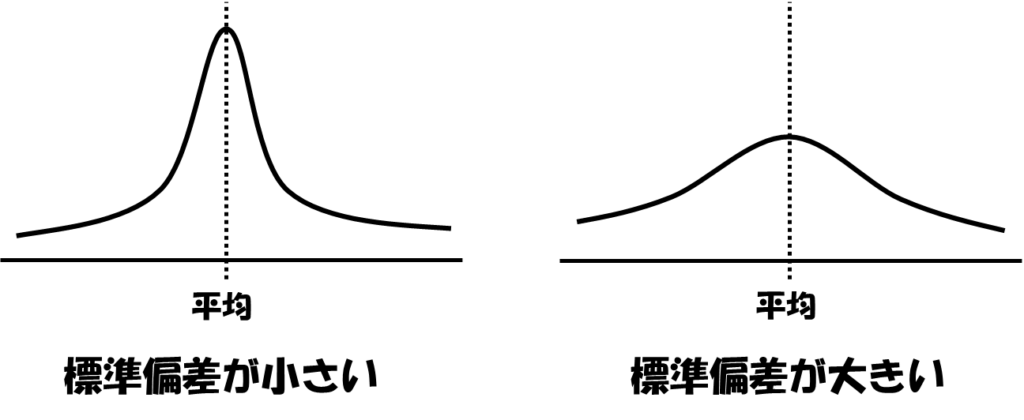
Zスコア
Zスコアとは、ある数値が平均からどれだけ上回っているか、下回っているかを示すものです。
どれだけ上回っているか・下回っているかは、何標準偏差分かで示しています。
もし、ある数値が平均よりも1標準偏差分上回っているならば、Zスコアは1ですね。
また、平均よりも0.4標準偏差分下回っているならば、Zスコアは0.4です。
Zスコアの出し方の式は、こんな感じ。

このZスコアならば、形が異なる正規分布同士でも、ある数値がどの位置にいるのかを標準化することができます。
正規分布が出てきたときには、Zスコアまですぐに出せるようになっておきたいものですね。
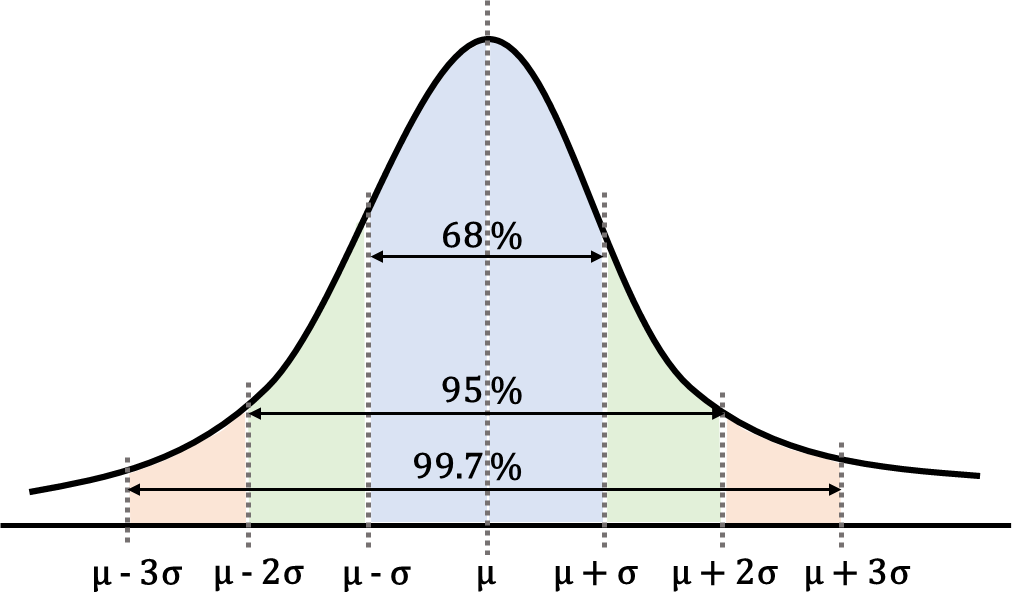
68:95:99.7の法則
何の数字?って思いますよね。
これは、平均から1,2,3標準偏差分離れた位置に納まる確率です。
平均から±1標準偏差以内に、数値が収まる確率は68%。
平均から±2標準偏差以内に、数値が収まる確率は95%。
平均から±3標準偏差以内に、数値が収まる確率は99.7%。
これを知っておくと、用いた数値が、正規分布の中でどれだけの位置にいるのかを知ることができます。
Zスコア算出の必要も無いので、実践の場で簡単に評価したいときなどに、よく使われるようです。
確率変数の分布の形 「二項分布」
有名な分布の形にはもう一つあります。
それが「二項分布」。
「二項分布」とは「ある一定回数の中で、何回成功するかの確率」を求められる分布です。
例えば、こんな感じ。
・コインを4回投げて3回表が出る確率
・サイコロを6回投げて1が1回出る確率
ここで、公式を示しちゃいますね。
結構複雑なので、できるだけ分かりやすく書くようにします。
まず求めたい事象を一般化。
「1回成功する確率をp、これをn回の試行において、k回成功する確率を求めたい」
次にこれらの文字を使って式にします。
この求めたい確率は、次の式。
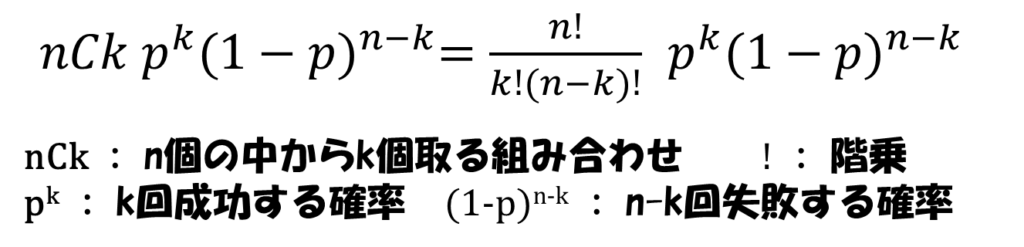
ただ日々色んな分布に触れていると、どの分布なのか・本当に二項分布なのか、という心配があると思います。
そこで、二項分布かどうかを確かめるために、以下の4つを確認すると良いでしょう。
1.試行は独立である(1回目の試行が2回目の試行に影響を及ぼさないか)
2.全試行回数はn回で固定されている。
3.それぞれの試行結果は「成功」「失敗」のどちらかである。(成功、失敗と見なせれば良い)
4.成功確率pはそれぞれの試行において同じである。
大分複雑ですよね。
ただ、公式は複雑ですが、具体例(コインやサイコロの例)を考えれば分かりやすいと思います。
データ分析を目指す方は、基本となる可能性が高いので、抑えておくと良いでしょう。
まとめ
今回は「データ分析のための統計学入門 第四章」をまとめました。
今回の記事をまとめると
・確率変数の分布で正規分布が、最も基本
・二項分布は「一定回数の試行のうち、何回成功するか」の確率を求められる
となります。
以下でさらっと、今回は取り上げなかった「幾何分布」「負の二項分布」「ポアソン分布」の説明もしておきますね。
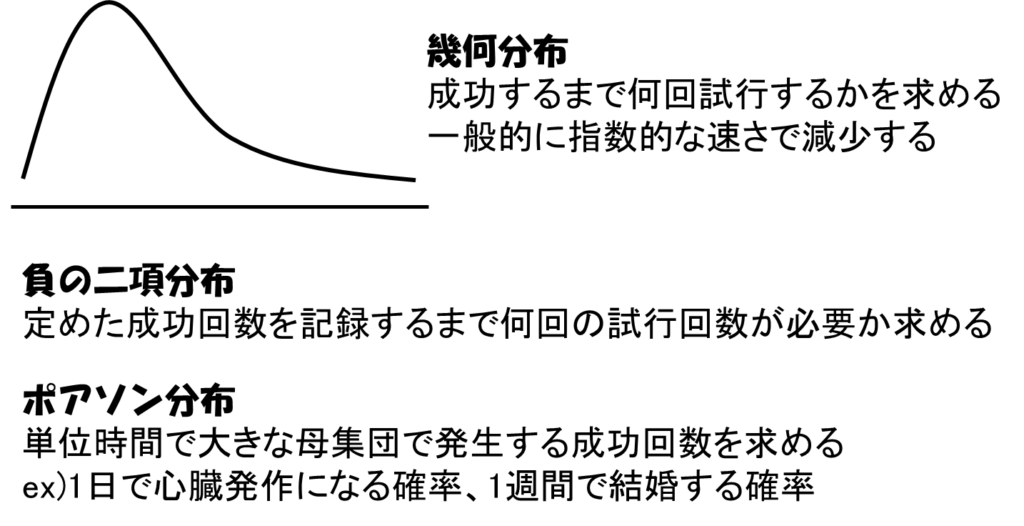
長いと思っていた「データ分析のための統計学入門」も、もうすぐで半分。
データ分析に興味がある人や、実際のその職に就こうとしている人の手助けになれば幸いです。
初心者から目指そうという方は一緒に頑張っていきましょう!
ではまた~










コメント