※本記事はアフィリエイト広告を含んでいます
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/214d380e.96fa3830.214d380f.9c4125c0/?me_id=1213310&item_id=20632239&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F8326%2F9784297128326_1_2.jpg%3F_ex%3D240x240&s=240x240&t=picttext "[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]")
どーも、りけーこっとんです。
DS検定の勉強をしよう！と思ったは良いものの、こんな悩みはありませんか？
DS検定ってどうやって勉強すればいいの？
DS検定の勉強の仕方が分からない…
本で勉強するのは分かるけど、高いなぁ…
無料で単語解説されているサイトとかないかな？
DS検定は、始まったばかりの試験だから、対策法とか分からないよね。
じゃあ、このサイトで出題範囲の内容を押さえていこう～
DS検定の解説をすぐ見たいよ！という方は、以下から最初の解説に飛べます。
今回はスキルチェックリスト
「DS２１：逆行列が算出でき、逆行列で連立方程式が解ける」と
「DS２２：固有ベクトル、固有値の意味を理解している」を解説していくよ～
本サイトでは超重要項目、重要項目、覚えておきたい項目と表記を分けますので、勉強時の参考にしてみてください。
DS検定って、そもそもどんな資格？という方は以下の記事をご覧くださいね。
試験範囲は以下の二つから出題されます。
・スキルチェックリスト
・数理、データサイエンス、AI（リテラシーレベル）モデルカリキュラム
本内容は以下の書籍を参考に作成しております。
なお、本サイトはDS検定の合格を保証するわけではありませんので、ご了承ください。
では早速、内容に入っていきましょう！
※「DS○○：」項目の文章は独自に短縮して表現しております
DS２１：逆行列が算出でき、逆行列で連立方程式が解ける
この項目は「逆行列」と「行列を用いた連立方程式の解き方」を理解しているか、という項目。
まず単位行列と行列式というキーワードを解説していきます。
これらは、逆行列を求める際に必須の知識なので、しっかり覚えましょう。
単位行列
行列の対角成分が全て1で、他が0の行列のこと。
以下のような式で表せる。
※行と列の数が同じ行列（正方行列）でないと単位行列になりません。
例
\(\displaystyle \left(
\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array}
\right), \left(
\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}
\right) \)
行列の世界での「１」みたいなものです
行列式
ベクトルなどを行列で線形変換した時に、空間が何倍になるかという数値。
detAや｜で囲んで表す。
※行と列の数が同じ行列（正方行列）でないと行列式は作れません。
2×2の行列式の計算イメージ
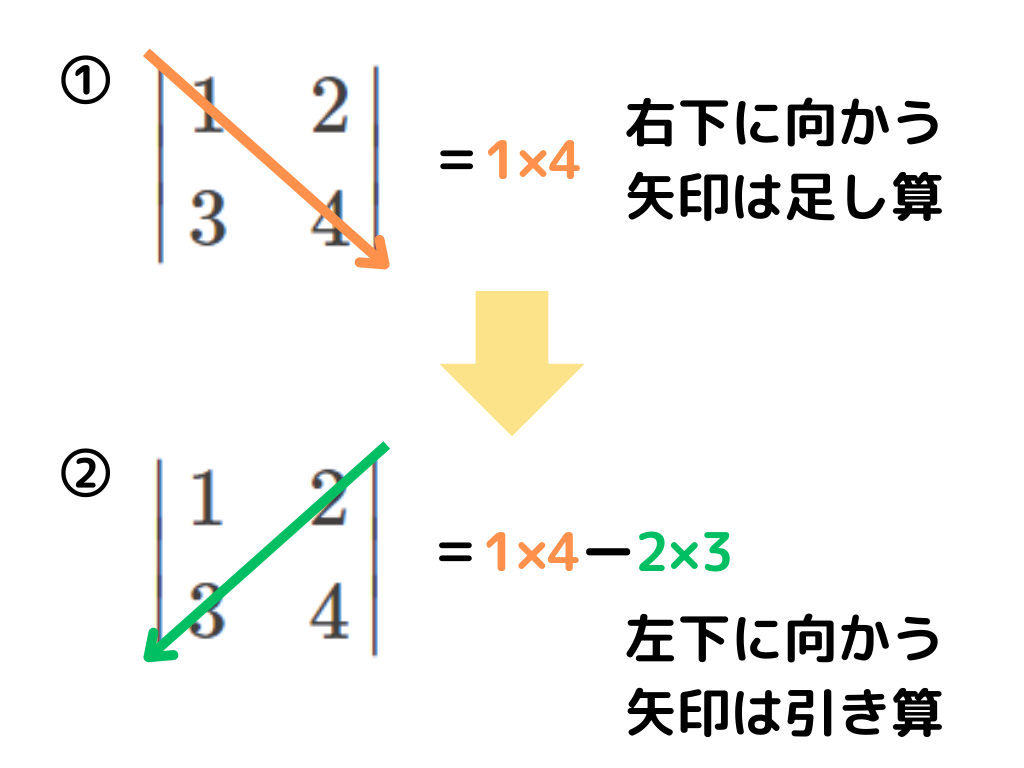
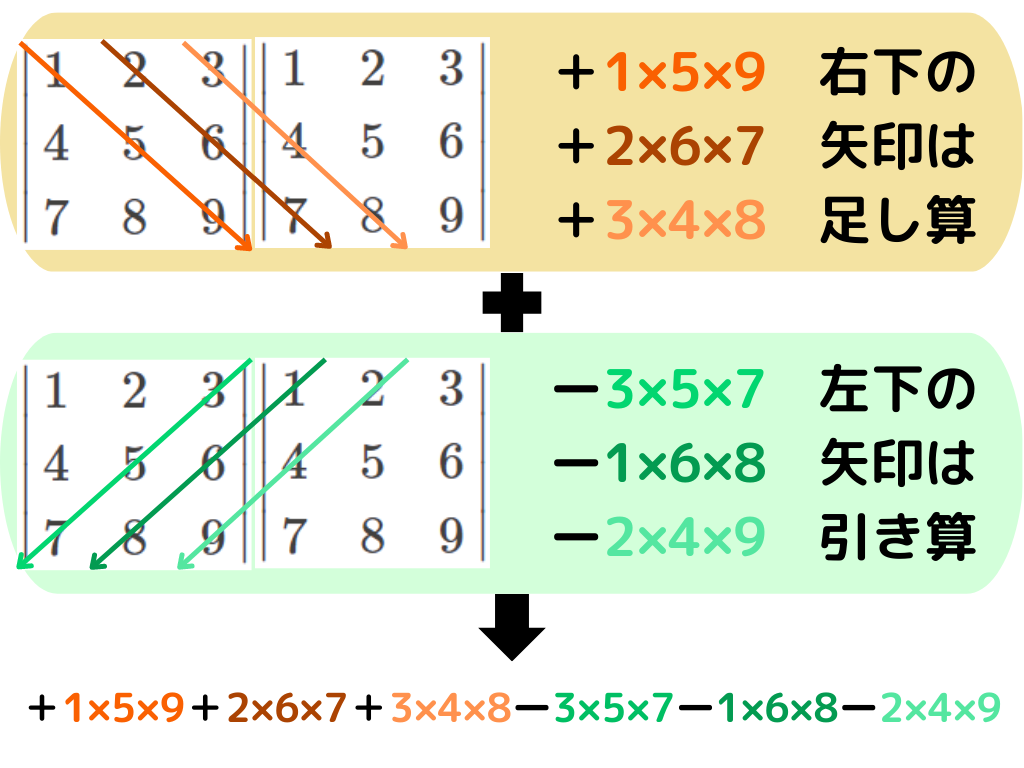
3×3の行列式の計算イメージ
１．同じ行列を二つ並べる
２．斜め（対角）成分を掛け算する
３．右矢印の掛け算は足し算、左矢印の掛け算は引き算する
線形変換？空間が何倍になるか？どういうこと？
これらの解説をし始めると長くなってしまうので、以下２つの記事に譲りますね。
※正直、りけーこっとんが教えるよりも分かりやすいと思いましたw
HEADBOOSTさんの記事は、他の数学知識も分かりやすくアニメーションを用いて解説して頂いています。
興味ある方は覗いてみると良いかと。
さて、「単位行列」「行列式」二つのキーワードを押さえたうえで、「逆行列」の解説に入ります。
逆行列
逆行列
ベクトルなどを行列Aで線形変換した後、その変換を元に戻す行列のこと。
数値でいうと、逆数の考え方に近い。
\(\displaystyle A^{-1} \)で表す。
元の行列を\(\displaystyle A\)
単位行列を\(\displaystyle I\)とすると
\(\displaystyle A\times A^{-1}\)も\(\displaystyle A^{-1}\times A \)も同じでしょ？
\(\displaystyle 1\times 2\)も\(\displaystyle 2\times 1\)も同じなんだから
\(\displaystyle I\)は単位行列で、数値の１と似ていましたね。
このことから、「逆行列」と「逆数」は似たイメージになります。
繰り返しになりますが、行列は「掛ける順番」が大事なので、\(\displaystyle A\times A^{-1}\)と\(\displaystyle A^{-1}\times A \)の二種類を定義しています。
逆行列の求め方
ここでは2×2の逆行列の求め方を紹介します。
逆行列の求め方(サラスの公式)
\(\displaystyle A = \left(
\begin{array}{cc}
a & b \\
c & d
\end{array}
\right) \)とすると
3×3行列以上の逆行列の求め方も、もちろんあります。
しかし、DS検定では2×2を覚えておけば十分です。
3×3行列以上の逆行列の求め方も知りたいという方は、「逆行列の求め方」というHEADBOOSTさんの記事をご覧ください。
このサイトでも機会があれば解説したいと思います。
逆行列で連立方程式を解く
逆行列は非常に便利で、連立方程式を解くときにも使えます。
連立方程式での行列の表し方は、以前の記事でも解説していますので、参考にしてみてください。
以下のような連立方程式であれば、
\begin{eqnarray}
\left\{
\begin{array}{l}
2x + y = 10 \\
x + 4y = 12
\end{array}
\right.
\end{eqnarray}
行列で表すと、こんな感じ。
$$\begin{align} \left( \begin{array}{cc} 2 & 1 \\ 1 & 4 \end{array} \right) \times \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{c} 10 \\ 12 \end{array} \right) \end{align}$$連立方程式を解くには、\(\displaystyle \left(
\begin{array}{cc}
2 & 1 \\
1 & 4
\end{array}
\right) \)の部分の逆行列を求める必要があります。
公式に従って求めてみましょう。
$$\begin{align} \frac{1}{ad-bc} \times \left( \begin{array}{cc} d & -b \\ -c & a \end{array} \right) & = \frac{1}{2\times 4-1\times 1} \times \left( \begin{array}{cc} 4 & -1 \\ -1 & 2 \end{array} \right) \\ & = \left( \begin{array}{cc} \frac{4}{7} & -\frac{1}{7} \\ -\frac{1}{7} & \frac{2}{7} \end{array} \right) \end{align}$$では、逆行列を連立方程式の両辺に左から掛けます。
$$\begin{align} \left( \begin{array}{cc} \frac{4}{7} & -\frac{1}{7} \\ -\frac{1}{7} & \frac{2}{7} \end{array} \right) \times \left( \begin{array}{cc} 2 & 1 \\ 1 & 4 \end{array} \right) \times \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{cc} \frac{4}{7} & -\frac{1}{7} \\ -\frac{1}{7} & \frac{2}{7} \end{array} \right) \times \left( \begin{array}{c} 10 \\ 12 \end{array} \right) \end{align}$$ $$\begin{align} \left( \begin{array}{cc} \frac{4}{7}\times 2 + (-\frac{1}{7}\times 1) & \frac{4}{7}\times 1 + (-\frac{1}{7}\times 4) \\ -\frac{1}{7}\times 2 + \frac{2}{7}\times 1 & -\frac{1}{7}\times 1 + \frac{2}{7}\times 4 \end{array} \right) \times \left( \begin{array}{c} x \\ y \end{array} \right) \\ = \left( \begin{array}{c} \frac{4}{7}\times 10 + (-\frac{1}{7}\times 12) \\ -\frac{1}{7}\times 10 + \frac{2}{7}\times 12 \end{array} \right) \end{align}$$ $$\begin{align} \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \times \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{cc} 4 \\ 2 \end{array} \right) \end{align}$$最後の行列を掛け算すると分かりますが、\(\displaystyle x=4, y=2\)となっています。
これは、連立方程式の解ですね。
不安な方は式に代入して、計算してみてください。
DS２２：固有ベクトル、固有値の意味を理解している
この項目は、固有ベクトルと固有値が説明できますか？という項目。
それぞれどんな意味なのか見ていきましょう。
固有ベクトル
固有ベクトル
行列Aを掛けても向きが変わらず、長さしか変わらないベクトルのこと。
「行列Aの固有ベクトル」という。
以下の式の\(\displaystyle \vec{x} \)のこと。
定義式
\(\displaystyle A\vec{x} = \lambda \vec{x} \)
では、\(\displaystyle \left(
\begin{array}{c}
1 \\
1
\end{array}
\right) \)というベクトルに、どんな行列を左から掛けたら、向きが変わらないのでしょうか？
答えは、\(\displaystyle \left(
\begin{array}{cc}
1 & 2 \\
2 & 1
\end{array}
\right) \)です。
本当？と思う方は、計算してみてください。
\(\displaystyle \left(
\begin{array}{c}
3 \\
3
\end{array}
\right) \)というベクトルになって、二次元座標で表すと以下のような感じにあるはずです。
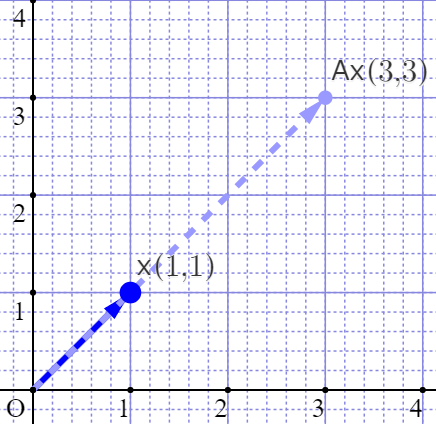
この計算方法については、固有値も解説した後に解説しますね。
固有値
固有値
固有ベクトルに行列Aを掛けた時の、長さの変化量（\(\displaystyle \lambda \)倍）のこと。
「行列Aの固有値」という。
以下の式の\(\displaystyle \lambda \)のこと。
定義式
\(\displaystyle A\vec{x} = \lambda \vec{x} \)
つまり固有ベクトルに行列Ａを掛けても、”固有値（\(\displaystyle \lambda \)）”倍になるだけで、向きは変わりません。
先ほどと同じ例を見ていきましょう。
\(\displaystyle \vec{x} = \left(
\begin{array}{c}
1 \\
1
\end{array}
\right) \)というベクトルがあったとします。
まずは定義式の左側（\(\displaystyle A\vec{x}\)）から計算しましょう。
\(\displaystyle \left(
\begin{array}{cc}
1 & 2 \\
2 & 1
\end{array}
\right) \times \left(
\begin{array}{c}
1 \\
1
\end{array}
\right) = \left(
\begin{array}{c}
3 \\
3
\end{array}
\right) \)
となりますよね。
ここで\(\displaystyle \vec{x} = \left(
\begin{array}{c}
1 \\
1
\end{array}
\right) \)と\(\displaystyle \vec{x} = \left(
\begin{array}{c}
3 \\
3
\end{array}
\right) \)はどんな関係にあるでしょうか？
単純に３倍されていますよね。
つまり定義式の右側（\(\displaystyle \lambda \vec{x}\)）の\(\displaystyle \lambda \)は３となるわけです。
このように行列を掛けた時に、固有値ベクトル\(\displaystyle \vec{x}\)が何倍になったかを表すのが固有値です。
図で表すと先ほどと同じ図になり、矢印の長さが３倍になっていることが分かるでしょう。
固有値・固有ベクトルの求め方
先ほどまでは解説のために固有ベクトルがある前提で考えました。
しかし、実際には「行列Aの固有値と固有ベクトルを求めよ」みたいに問われます。
「行列がある ⇒ 固有値・固有ベクトルを求める」という問題になるので、注意してください。
つまり先ほどの例でいうと、\(\displaystyle \left(
\begin{array}{cc}
1 & 2 \\
2 & 1
\end{array}
\right) \)という行列の「固有値」「固有ベクトル」を求めよ、となるわけです。
固有値・固有ベクトルの求め方
１．\(\displaystyle A\vec{x} = \lambda \vec{x} \)を左辺にまとめて、\(\displaystyle (A – \lambda I) \vec{x} = 0 \)とする。
※ここでの\(\displaystyle I\)は単位行列です。
単位行列は数値の１と似た感じなので、掛けても行列が変わることはありません。
２．\(\displaystyle A – \lambda I = 0 \)を解いて、固有値\(\displaystyle \lambda \)を求める。
３．\(\displaystyle (A – \lambda I) \vec{x} = 0 \)の\(\displaystyle \lambda \)に求めた固有値を代入して、\(\displaystyle \vec{x} \)を求める。
実際に問題を解きながら、計算イメージをしましょう。
１．\(\displaystyle A\vec{x} = \lambda \vec{x} \)を左辺にまとめて、\(\displaystyle (A – \lambda I) \vec{x} = 0 \)とする。
\(\displaystyle (A – \lambda I) \vec{x} = 0 \)に実際に数字を入れていきます。
$$\Bigl(\left( \begin{array}{cc} 1 & 2 \\ 2 & 1 \end{array} \right) – \lambda \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right)\Bigl) \left( \begin{array}{c} x_1 \\ x_2 \end{array} \right) = 0$$２．\(\displaystyle A – \lambda I = 0 \)を解いて、固有値\(\displaystyle \lambda \)を求める。
\(\displaystyle A – \lambda I = 0 \)を解きます。
行列と数値（\(\displaystyle \lambda \)）の掛け算は、行列の全ての要素に\(\displaystyle \lambda \)を掛ければ良いので、
\(\displaystyle \left(
\begin{array}{cc}
1 & 2 \\
2 & 1
\end{array}
\right) – \lambda \left(
\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array}
\right) = 0\)
\(\displaystyle \left(
\begin{array}{cc}
1 & 2 \\
2 & 1
\end{array}
\right) – \left(
\begin{array}{cc}
\lambda & 0 \\
0 & \lambda
\end{array}
\right) = 0\)
\(\displaystyle \left(
\begin{array}{cc}
1-\lambda & 2 \\
2 & 1-\lambda
\end{array}
\right) = 0\)
次に行列式を求めた後に、因数分解を経て固有値を求めます。
\(\displaystyle (1-\lambda)^2 – 4 = 0\)
\(\displaystyle (1-2\lambda +\lambda^2) – 4 = 0\)
\(\displaystyle \lambda^2 -2\lambda – 3 = 0\)
\(\displaystyle (\lambda +1)(\lambda – 3) = 0\)
\(\displaystyle \lambda = 3, -1\)
因数分解のやり方が分からない！という方は「因数分解とは？｜テラコヤプラスby Abema」をご覧ください。
３．\(\displaystyle (A – \lambda I) \vec{x} = 0 \)の\(\displaystyle \lambda \)に求めた固有値を代入して、\(\displaystyle \vec{x} \)を求める。
\(\displaystyle \lambda = 3\)の場合
\(\displaystyle (A – \lambda I) \vec{x} = 0 \)
$$\Bigl(\left( \begin{array}{cc} 1 & 2 \\ 2 & 1 \end{array} \right) – \lambda \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right)\Bigl) \left( \begin{array}{c} x_1 \\ x_2 \end{array} \right) = 0 $$ $$\left( \begin{array}{cc} 1-3 & 2-0 \\ 2-0 & 1-3 \end{array} \right) \left( \begin{array}{c} x_1 \\ x_2 \end{array} \right) = 0 $$ $$\left( \begin{array}{cc} -2 & 2 \\ 2 & -2 \end{array} \right) \left( \begin{array}{c} x_1 \\ x_2 \end{array} \right) = 0$$最後の式に行列の掛け算を行って、普通の式に直すと
\begin{eqnarray}
\left\{
\begin{array}{l}
-2x_1 + 2x_2 = 0 \\
2x_1 – 2x_2 = 0
\end{array}
\right.
\end{eqnarray}
と二つの式が出てきますね。
しかし下の式の両辺に「-」を掛けると分かりますが、どちらも同じ式です。つまり、
\(\displaystyle -2x_1 + 2x_2 = 0 \)
\(\displaystyle -2x_1 = -2x_2 \)
\(\displaystyle x_1 = x_2 \)
\(\displaystyle x_1 = x_2 \)であれば数字は何でもいいので、任意定数（数値なら何でも良いですよという意味）\(\displaystyle a \)を掛けます。
結果的に固有ベクトルは\(\displaystyle a \left(
\begin{array}{c}
1 \\
1
\end{array}
\right) \)と求まりますね。
\(\displaystyle \lambda = -1\)の場合も同じように求められます。
答えは\(\displaystyle b \left(
\begin{array}{c}
1 \\
-1
\end{array}
\right) (bは任意定数)\)
まとめ
今回は「逆行列・固有ベクトル・固有値」などを解説してきました。
以下の項目を説明できるようになっているでしょうか？
・単位行列
・逆行列
・逆行列の求め方
・固有ベクトル
・固有ベクトルの求め方
・固有値
・固有値の求め方
DS検定は覚える内容が多いです。
一つ一つを細部まで見るというよりは、広く浅く見ていくことが重要かと思います。
DS検定を取得して、データサイエンティストやAI関連の仕事への道を開きましょう！
次回は「微分・偏微分」などについて解説していきます。
ではまた～
DS検定の続きの解説は以下のページからどうぞ！
コメント