※本記事はアフィリエイト広告を含んでいます

どーも、りけーこっとんです。
「G検定取得してみたい!」「G検定の勉強始めた!」
このような、本格的にデータサイエンティストを目指そうとしている方はいないでしょうか?
また、こんな方はいませんか?
「なるべく費用をかけずにG検定取得したい」「G検定の内容について網羅的にまとまってるサイトが見たい」
今回はG検定の勉強をし始めた方、なるべく費用をかけたくない方にピッタリの内容。
りけーこっとんがG検定を勉強していく中で、新たに学んだ単語、内容をこの記事を通じてシェアしていこうと思います。
結構、文章量・知識量共に多くなっていくことが予想されます。
そこで、超重要項目と重要項目、覚えておきたい項目という形で表記の仕方を変えていきたいと思いますね。
早速G検定の中身について知りたいよ!という方は以下からどうぞ。

具体的にどうやって勉強したらいいの?
G検定ってどんな資格?
そんな方は以下の記事を参考にしてみてください。
なお、りけーこっとんは公式のシラバスを参考に勉強を進めています。
そこで主な勉強法としては
分からない単語出現 ⇒ web検索や参考書を通じて理解 ⇒ 暗記する
この流れです。
皆さんも一緒に頑張りましょう!
※この記事は合格を保証するものではありません
大項目「ディープラーニングの概要」
G検定のシラバスを見てみると、試験内容が「大項目」「中項目」「学習項目」「詳細キーワード」と別れています。
本記事は「大項目」の「ディープラーニングの概要」の内容。
その中でも「最適化・その他のテクニック」というところに焦点を当ててキーワードを解説していきます。
G検定の大項目には以下の8つがあります。
・人工知能とは
・人工知能をめぐる動向
・人工知能分野の問題
・機械学習の具体的な手法
・ディープラーニングの概要
・ディープラーニングの手法
・ディープラーニングの社会実装に向けて
・数理統計
とくに太字にした「機械学習とディープラーニングの手法」が多めに出るようです。
今回はディープラーニングの概要ということもあって、ディープラーニングの基礎的な内容。
ここを理解していないと、ディープラーニングがどういうものかを理解できません。
ここから先の学習の理解を深めるために、そしてG検定合格するために、しっかり押さえておきましょう。
今回はモデル最適化の手法や、ディープラーニングにおける他のテクニックを紹介していきますね。
まずは具体的なテクニックを見る前に、ディープラーニングで見られる現象・定理について見ていきましょう。
過学習
既に複数回出てきているとは思いますが、復習の意味も兼ねて載せています。
過学習とは学習を行いすぎて、訓練データへの当てはまりが異常に良くなってしまう現象。
過学習が起こると、未知データへの当てはまり(予測精度)が悪くなってしまいます。
訓練データと未知データへの予測精度のグラフは以下の通り。
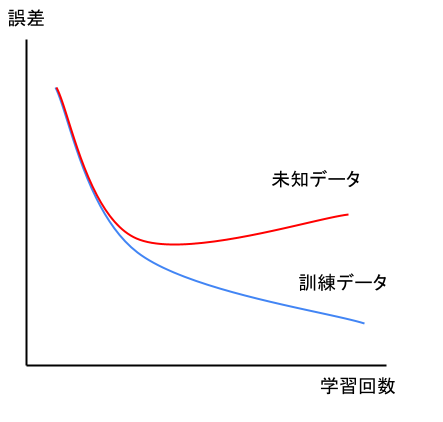
過学習の点を通り過ぎると、訓練データに対しては誤差が下がりますが、未知データへの誤差は大きくなっています。
このようにしてみると、過学習になった瞬間が一目で分かりますね。
ノーフリーランチの定理
ノーフリーランチの定理は、どんな問題に対しても万能なアルゴリズムは存在しない定理のこと。
David H. WolpertさんとWilliam G. Macreadyさんが提唱した定理のようです。
特定の領域では優れた性能を発揮しても、それ以外の問題領域では性能が下がってしまう。
これは、感覚的にも理解しやすい定理なのではないでしょうか。
二重降下現象
二重降下現象とは、深層学習において二段階で誤差が低下する現象のこと。
言い換えると、パフォーマンス(予測精度)は最初は向上するが、ある程度を越えると悪化し始める(過学習的な)。
しかし、さらに訓練時間やデータ量を増やしていくと予測精度が再び向上する
ということになりますね。
これをグラフにしてみると以下の様な形になります。
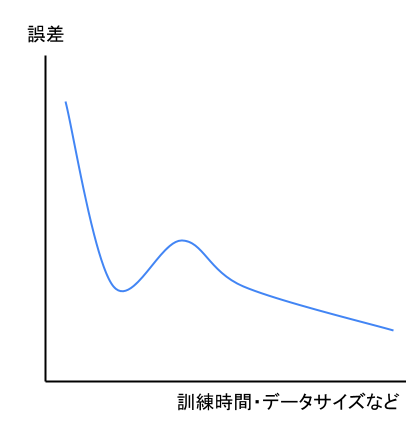
この現象がなぜ起こるかは、まだ解明されていないようです。
早期終了
さて、ここからモデルの最適化やその他のテクニックを見ていこうと思います。
早期終了とは、過学習になってしまう前に学習をやめるテクニック。
ディープラーニングでは、過学習を起こすことが多いです。
そこで過学習を起こす前に早めに学習をやめておけば、最良とは言わなくても、ある程度の精度のモデルを得ることが可能ですよね。
ディープラーニングのようにモデルが複雑になると、ハイパーパラメータを求めることが非常に難しくなります。
なので無理に最良のモデルを得ようとして過学習するよりは、そこそこの精度のモデルの方が汎用性が高いということです。

バッチ正規化
バッチ正規化とは、主にニューラルネットワーク、CNNで用いられる正規化のこと。
CNNについては、後の範囲で詳しく触れたいと思います。
CNNは「畳み込み層」「プーリング層」「全結合層」の三層から成っているんですね。
「畳み込み層」「プーリング層」は少し特殊な層です。
「全結合層」は普通のニューラルネットワークと同じ構造で、出入力層・隠れ層を持ちます。
学習の順序としては
「畳み込み」→「プーリング」→「畳み込み」→「プーリング」→・・・→「全結合」
となっています。
このような学習ではそれぞれの層を重ねる毎に、元データの分布が偏りやすくなってしまいます。
そこで各層で伝わってきたデータに対し、定期的に正規化を行うことでデータの偏りを無くし、より良いモデルを作る手法をバッチ正規化と言うようです。
イメージは以下の様な感じ。
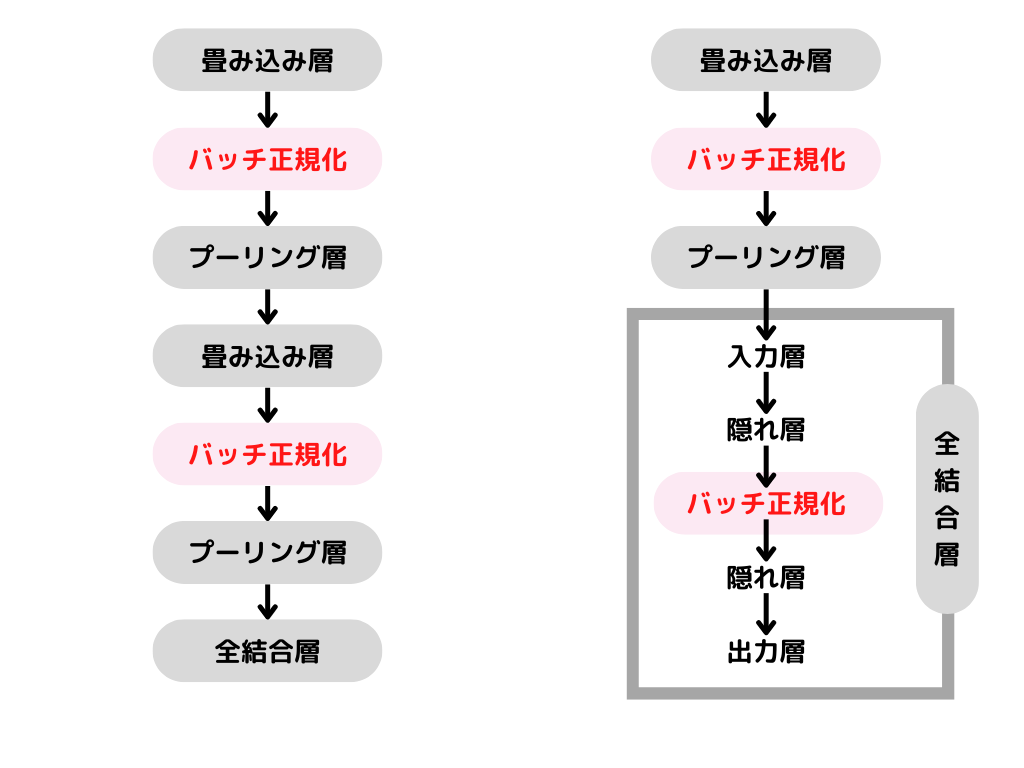
もっと厳密にすると違うのですが、こんな感じのイメージで覚えておくと良いかと。
左のパターンと右のパターンどちらも使われるようです。
正規化とは、データのスケールを合わせることで「正則化・標準化」等があります。
詳しくは後述します。
バッチ正規化の特徴としては以下の三つ。
・学習の進行速度を早くする
・初期値への依存が少ない
・過学習を抑制する
このようにしてモデルを最適化する方法もあります。
アンサンブル学習
アンサンブル学習は、複数の弱い学習器を使い、一つの強い学習器を作る方法。
弱い学習器というのは、汎化性能が高くない学習器のことです。
逆に強い学習器とは、汎化性能が高い学習器のこと。
つまり、汎化性能が低い学習器を組み合わせて、汎化性能を上げる学習方法ということになりますね。
詳しくは以下の記事でも説明しているので、気になる方はご覧ください。
ドロップアウト
ドロップアウトとは、ニューラルネットワークで学習を進める際の、モデル最適化手法の一つ。
やり方としては、隠れ層のノードをランダムに0にすることで、アクセスできないようにします。
すると擬似的に何個も違うニューラルネットワークの形ができ、精度が向上するという仕組みです。
イメージは以下の様な感じ。
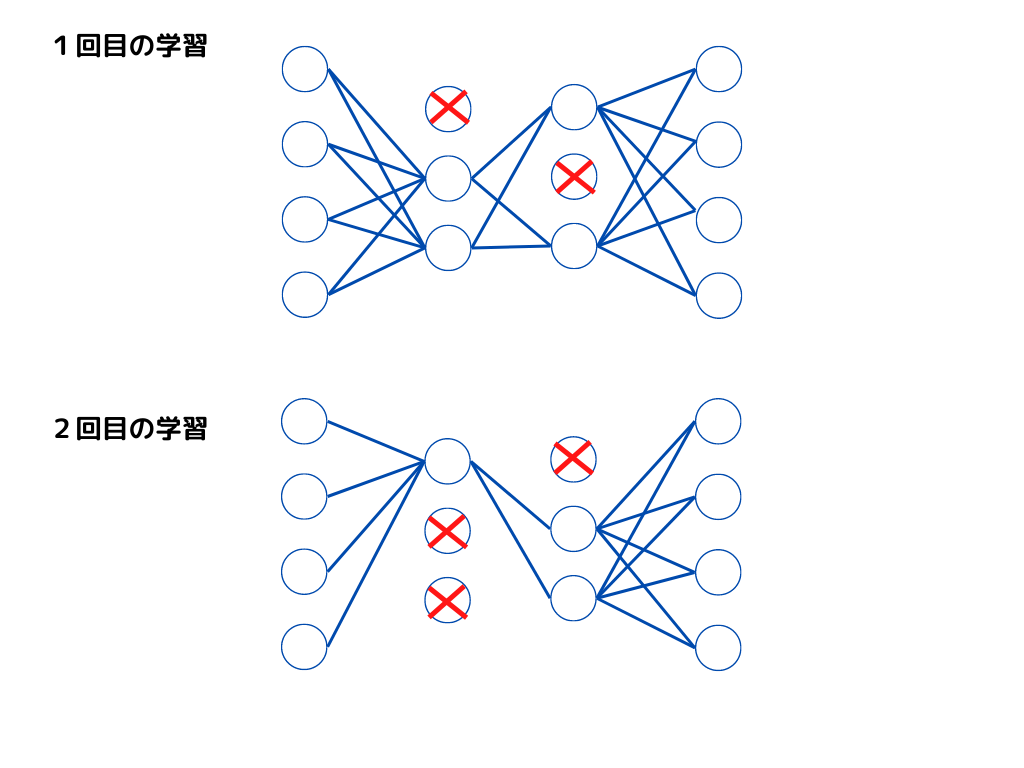
このように一回目と二回目では違うノードが削除されていますよね。
つまり一回目と二回目では違う形のニューラルネットワークということになります。
なので擬似的にアンサンブル学習ができて、良いモデルが作れると言うことですね。
正則化
正則化とは損失関数に正則化項(ペナルティ項)を追加することで、過学習を防ぐ方法。
代表的なものにはラッソ回帰や、
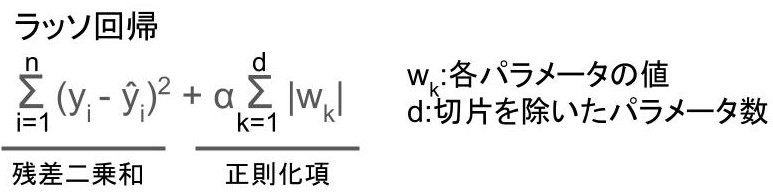
リッジ回帰があります。
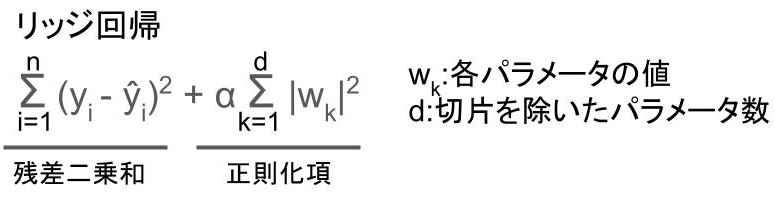
数式で難しそうに見えるかもしれませんが、「正則化項」という項が追加されているだけです。
「残差二乗和」はシンプルに「予測値と教師データの差」のことですね。
教師あり学習では「残差二乗和」を最小限にするように学習するわけですが、そこに「正則化項」を追加することで、過学習を防いでいるわけです。
正則化と正規化は言葉が似ているので、しっかり区別して覚えるようにしてください。
正規化は、説明変数同士の数値スケールを合わせることで学習させやすくすること。
正則化は、損失関数に正則化項を追加することで過学習を防ぐ方法。
標準化
標準化とは正規化の一種で、元データの平均を0、標準偏差を1にすること。
具体的な式は以下の通り。
$$ 標準化後のデータ = \frac{x_i-\mu}{\sigma} $$ $$x_{i}: 各データ$$ $$\mu: 平均値$$ $$\sigma: 標準偏差$$標準化を正規化ということもあるので、問題文を読むときに気を付けましょう。
スケールを統一するという意味では、正規化と同じですが、行う操作が異なる点に注意して覚えるようにしてください。
ちなみに単純に正規化といった場合は、以下のことを指すことが多いようです。
$$ 正規化後のデータ = \frac{x_i-x_{min}}{x_{max}-x_{min}} $$ $$x_{i}: 各データ$$ $$x_{min}: 最小値$$ $$x_{max}: 最大値$$りけーこっとんは最初、「正規化」「標準化」「正則化」が紛らわしすぎて苦労しました。
これらの言葉は機械学習以外の分野でも用いられます。
その分野ごとに定義が違うことがあるので、機械学習分野ではこの定義だと覚えておきましょう。
白色化
白色化とは、無相関化したn個の変数を持つデータの各変数の平均を0、分散を1にすること。
具体的な手順は以下の様になります。
1.無相関化
2.平均を0にする
3.分散を1にする
無相関化とは変数同士の相関を無くすこと。
数学的に言うと、共分散を0にすることを指します。
そして平均を0にするためには、それぞれのデータから平均値を引けばOKです。
最後に分散を1にするには、全データを分散値で割ってあげれば白色化の完了ですね。
平滑化
平滑化とは、画像データからノイズを除去すること。
一般的には
「連続的なデータ処理において、他のデータよりも大きく乖離しているデータを平均化、あるいは除去することにより、合理性を保つこと。」(参考:平滑化とは コトバンク)
という定義のようですね。
つまり外れ値を除去したり、他の値に近づけることで、全体的に突出の無い状態にするということ。
この操作を画像に対して行うと、ノイズを除去できるというわけです。
まとめ
今回は大項目「ディープラーニングの概要」の中の一つ「最適化とその他のテクニック」についての解説でした。
本記事の重要キーワードは以下の通り。
・過学習
・ノーフリーランチの定理
・二重降下現象
・早期終了
・バッチ正規化
・アンサンブル学習
・ドロップアウト
・正則化
・標準化
・白色化
・平滑化
以上が大項目「ディープラーニングの概要」の中の一つ「最適化とその他のテクニック」の内容でした。
ディープラーニングに関しても、細かく学習しようとするとキリがありませんし、専門的過ぎて難しくなってきます。
そこで、強化学習と同じように「そこそこ」で理解し、あとは「そういうのもあるのね」くらいで理解するのがいいでしょう。
そこで以下のようなことが重要になってくるのではないかと。
・ディープラーニングの特徴(それぞれの手法はどんな特徴があるのか)
・それぞれの手法のアルゴリズム(数式を覚えるのではなく、何が行われているか)
・何に使用されているのか(有名なもののみ)
ディープラーニングは様々な手法があるので、この三つだけでも非常に大変です。
しかし、学習を進めていると有名なものは、何度も出てくるので覚えられるようになります。
後は、新しい技術を知っているかどうかになりますが、シラバスに載っているものを押さえておけば問題ないかと。
次回は「ディープラーニングの手法」の「畳み込みニューラルネットワーク」に触れていきたいと思います。
覚える内容が多いですが、りけーこっとんも頑張ります!
ではまた~

続きは以下のページからどうぞ!











コメント
正則化と正規化の定義が若干ずれていると思いました。
細かく言うとややこしいので、ここでは機械学習に特化した説明に変更した方が良いと思います。
正則化は過学習を防ぐための手法。としておいてラッソやリッジ回帰の定数を出す方がわかりやすと思いました。
ご意見ありがとうございます!
確かに正則化の説明がずれていますね…
過学習を防ぐための手法が「正則化」、データのスケールを整えて学習しやすくするのが「正規化」ですね
参考にさせて頂きます、ありがたいです!