※本記事はアフィリエイト広告を含んでいます

どーも、りけーこっとんです。
「G検定取得してみたい!」「G検定の勉強始めた!」
このような、本格的にデータサイエンティストを目指そうとしている方はいないでしょうか?
また、こんな方はいませんか?
「なるべく費用をかけずにG検定取得したい」「G検定の内容について網羅的にまとまってるサイトが見たい」
今回はG検定の勉強をし始めた方、なるべく費用をかけたくない方にピッタリの内容。
りけーこっとんがG検定を勉強していく中で、新たに学んだ単語、内容をこの記事を通じてシェアしていこうと思います。
結構、文章量・知識量共に多くなっていくことが予想されます。
そこで、超重要項目と重要項目、覚えておきたい項目という形で表記の仕方を変えていきたいと思いますね。
早速G検定の中身について知りたいよ!という方は以下からどうぞ。

具体的にどうやって勉強したらいいの?
G検定ってどんな資格?
そんな方は以下の記事を参考にしてみてください。
なお、りけーこっとんは公式のシラバスを参考に勉強を進めています。
そこで主な勉強法としては
分からない単語出現 ⇒ web検索や参考書を通じて理解 ⇒ 暗記する
この流れです。
※この記事は合格を保証するものではありません
大項目「機械学習の具体的な手法」
G検定のシラバスを見てみると、試験内容が「大項目」「中項目」「学習項目」「詳細キーワード」と別れています。
本記事は「大項目」の「機械学習の具体的な手法」の内容。
その中でも「モデルの評価」というところに焦点を当ててキーワードを解説していきます。
G検定の大項目には以下の8つがあります。
・人工知能とは
・人工知能をめぐる動向
・人工知能分野の問題
・機械学習の具体的な手法
・ディープラーニングの概要
・ディープラーニングの手法
・ディープラーニングの社会実装に向けて
・数理統計
とくに太字にした「機械学習とディープラーニングの手法」が多めに出るようです。
本記事の範囲は、合格に向けては必須の基礎知識になります。
これから先の機械学習の理解を深めるために、そしてG検定合格するために、しっかり押さえておきましょう。
モデルの評価に関する内容が多くなってしまったので、記事を複数回に分割してお届けしようと思いますね。
モデルの評価というのは「作成したモデルが教師データや未知データに、どれだけ精度良く一致したか」を測るものになります。
つまり教師あり学習に用いられることが多い、というところは押さえておいてください。
精度評価指標はどこで使われるのか?
基本的には教師あり学習で用いられます。
教師あり学習の概要を以下に示しますね。
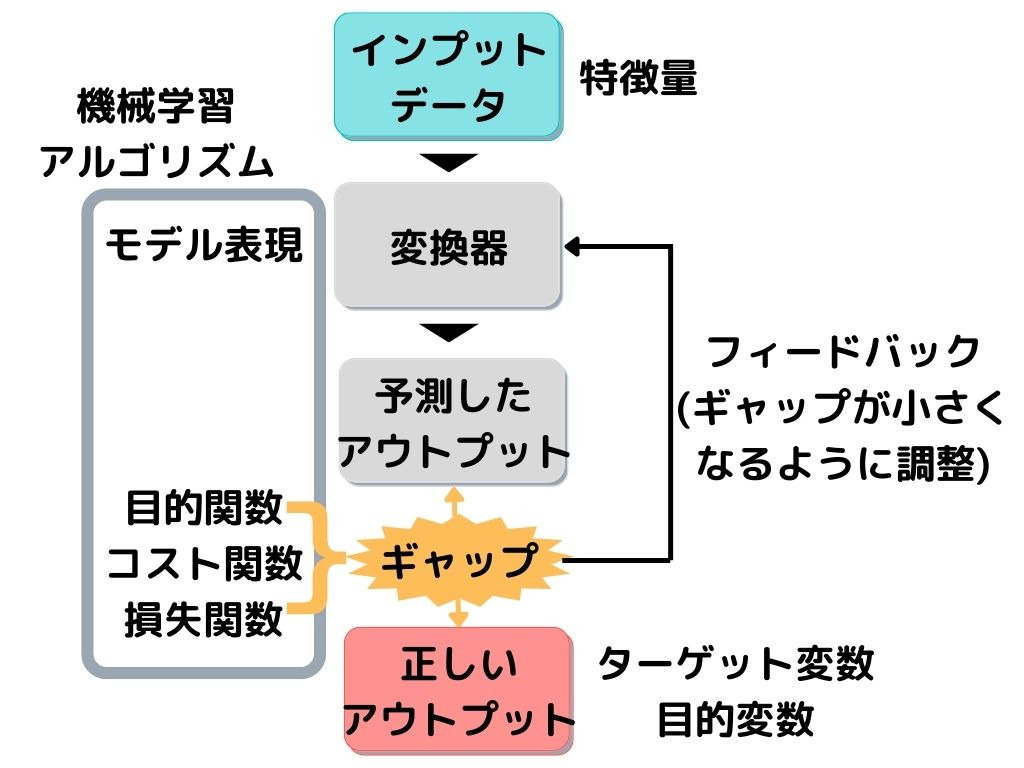
この図の「ギャップ」とある部分に、以下で紹介する精度評価指標が用いられます。
精度評価指標で出た「ギャップ(誤差)」が小さくなるように「変換器」を調整して、もう一回予測。
これを繰り返すことで、精度を高めて(ギャップを小さくして)いきます。
ホールドアウト検証
ホールドアウト検証とは、モデル検証におけるデータ分割手法の一種。
手持ちのデータを「学習データ」と「テストデータ」に分け、手元のデータだけでテストまで行うモデル検証法です。
モデルは、未知データをどれだけ精度よく予測できるかが重要でしたよね。
ただ未知データは「未知」なので、モデル作成時点で手元にはありません。
そこで手持ちのデータの一部を「未知データ」に見立てて、「テストデータ」として扱います。
こうすることで、手持ちのデータだけでモデルの作成を行い、評価までできるようになりますね。
交差検証
交差検証とはホールドアウト検証と同じく、モデル検証のためのデータ分割手法。
その中でも代表的なものが、k‐分割交差検証法です。
具体的な検証方法は以下の通り。
1.データをk個に分ける
2.そのうち一つをテストデータとする
3.残りを学習データとする
4.目的関数算出
5.k個のデータ全てが一回ずつテストデータになるまで2~4を繰り返す
6.全ての平均値を精度とする
イメージとしては以下のような感じ。
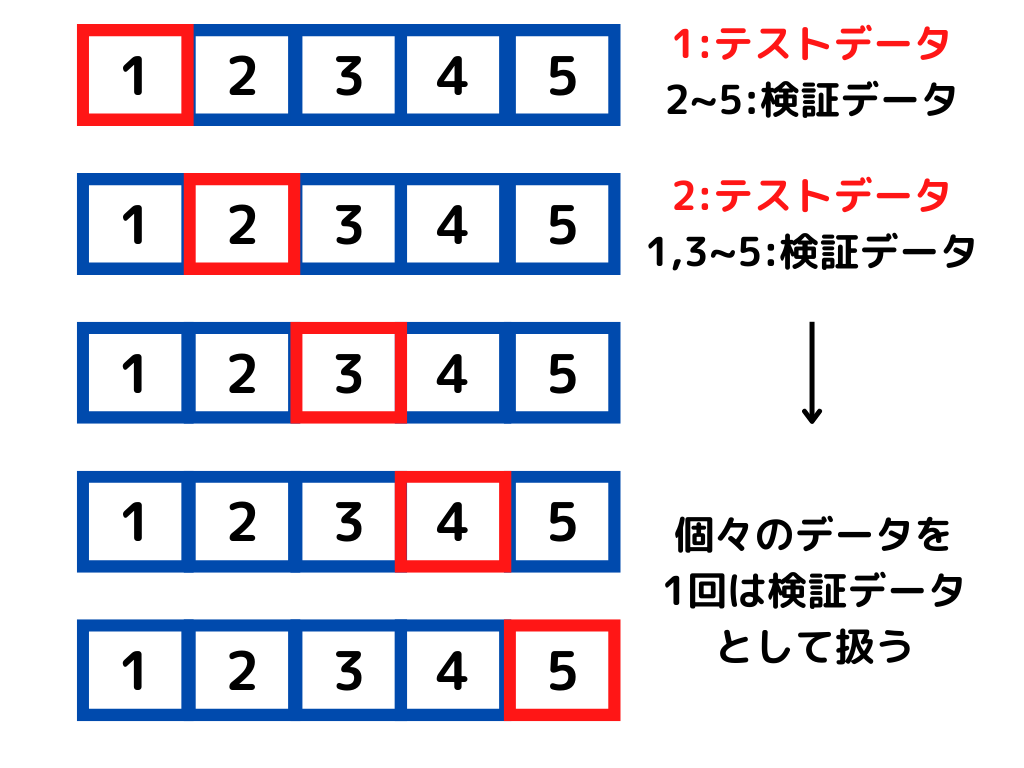
このように手持ちのデータを何個にも分けて検証を行うため、計算量は非常に多くなります。
しかし、データ数がそもそも少ない場合は、ホールドアウト検証よりもk‐分割交差検証のほうがいいでしょう。
データ数が少なければ、一回の学習・検証だけでは十分な精度が出ない可能性があるためです。
誤差関数
誤差関数とは、教師あり学習における目的関数・損失関数などと同義。
つまり、主には誤差関数の最小化が「教師あり学習」の目的になります。
この「誤差」には教師データと未知データで、異なる呼ばれ方をします。
汎化誤差
汎化誤差とは、未知データに対して生じる誤差のこと。
汎化誤差を小さくできれば、予測を外しにくい優れたモデルと言えるでしょう。
未知データに対する予測性能を汎化性能ということもあるので、覚えておきたいですね。
訓練誤差
訓練誤差とは、教師データ(テストデータ)に対して生じる誤差のこと。
テストデータに対する誤差なので、訓練誤差が大きいままだと汎化性能が良くなるわけはなく、学習が足りません。
しかし、テストデータに適応しすぎても汎化性能が悪くなってしまうので、注意が必要です。
具体的には次の「過学習・未学習」で説明します。

過学習・未学習
過学習とは学習用データを学習しすぎて、未知データの予測精度が悪くなっている状態。
未学習とは学習が少なすぎて、学習データにさえ当てはまりが悪い状態のこと。
イメージは以下の図のような感じ。
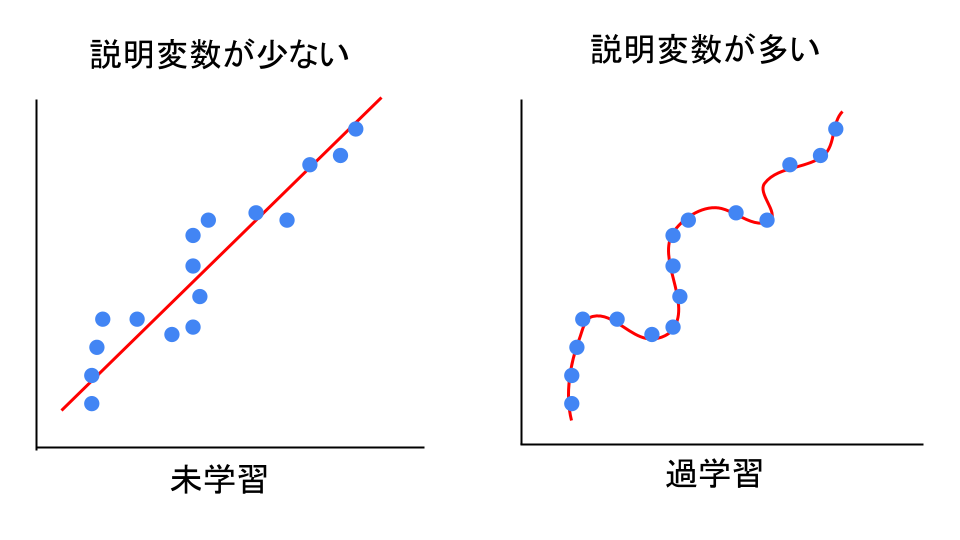
過学習も未学習も「未知データ」への精度の悪さという点では同じです。
どちらも起こらないように学習することが、モデル作成において重要ですね。
正則化
正則化とは、損失関数に正則化項(ペナルティ項)を追加することで、過学習を防ぐ方法。
損失関数に適用するので、基本的には「教師あり学習」で用いられる手法になりますね。
主な正則化には、追加する正則化項の種類によって以下のように変わってきます。
・L0正則化
・L1正則化
・L2正則化
それぞれ見ていきましょう。
L0正則化
L0正則化とは、正則化項にパラメータの絶対値の0乗を加える正則化手法。
実際の式は以下のような感じ。
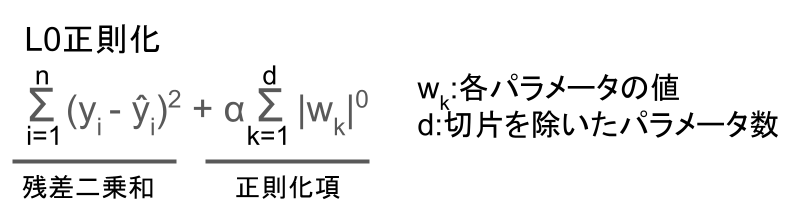
パラメータの大きさが0でない限り、正則化項は0乗しているので1になります。
つまり、パラメータ(重み係数)の大きさが0ではない個数をα倍したものを加える、という意味ですね。
L1正則化
L1正則化とは、正則化項にパラメータの絶対値の1乗を加える正則化手法。
代表的なものにラッソ回帰があります。
具体的な式は以下の通り。
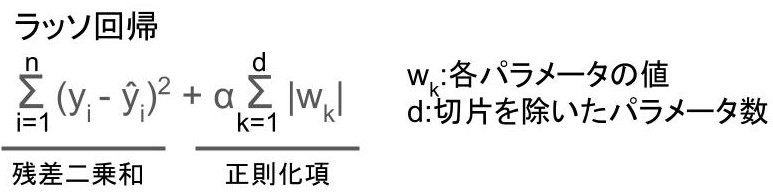
上記の式を目的関数として、最小化するようにモデルを学習。
不要なパラメータを0にするので、特徴量選択と次元圧縮に有効です。
さらに0の要素が非常に多い(スパースな)行列やデータに、教師あり学習を適用したいときに有効なようですね。
L2正則化
L2正則化とは、正則化項にパラメータの絶対値の2乗を加える正則化手法。
代表的なものにリッジ回帰があります。
具体的な式は以下の通り。
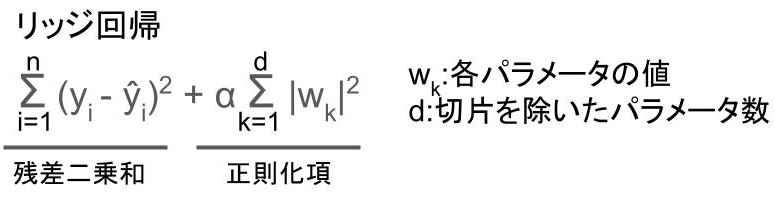
上記の式を目的関数として、最小化するようにモデルを学習。
パラメータを大きさに応じて0に近づけるようです。
ラッソ回帰と違って0にするのではなく、「0に近づける」ので注意。
学習率
学習率とは機械学習の最適化において、一回の学習でどれだけ値を動かすかのパラメータのこと。
学習率はハイパーパラメータであり、分析者自身が決めるパラメータです。
大きすぎると最適化が終わらず、小さすぎると最適化に時間がかかってしまいます。
教師あり学習の中でもG検定メインの範囲である「ディープラーニング」で用いられるパラメータです。
後の「ディープラーニング」の範囲でも出てくるので、押さえておきましょう。
モデルの解釈性
モデルの解釈性とは機械が何を根拠に、その出力をしたのかが人間にとって分かりやすいかどうかということ。
ディープラーニングなどのモデルは、予測精度が非常に高い分、中身が複雑です。
中身が複雑だと「出力が性格なのは良いけど、何を根拠にこの出力になったのか?」ということが、分かりにくくなってしまいますよね。
そのためモデルの解釈性は、ディープラーニングなど複雑なモデルを扱うときに、非常に重要な要素です。
LIME
LIMEとは、ブラックボックスモデルの解釈性を上げる技術の一つ。
ブラックボックスモデルとは中身が複雑で、中で何が起こっているかわかりにくくなったモデルのことです。
元の機械学習モデルとテストデータによって線形モデルを作成し、線型モデルの係数から特徴量の重要性を説明します。
つまりディープラーニングなどで学習したときに、どの特徴量の影響が大きかったかを説明できる技術となっているようですね。
SHAP
SHAPとは、ブラックボックスモデルの解釈性を上げる技術の一つ。
各特徴量を平均値に移動し、その変化度合いから特徴量の寄与度を求めるという方法のようです。
最終的にわかることとしては、LIMEと一緒でしょう。
LIMEの後に出てきた手法ということは押さえておきたいですね。
まとめ
今回は大項目「機械学習の具体的な手法」の中の一つモデルの評価についての解説、第三弾でした。
本記事の重要キーワードは以下。
・ホールドアウト検証
・k-分割交差検証
・誤差関数
・汎化誤差
・訓練誤差
・過学習、未学習
・L0、L1、L2正則化
・ラッソ回帰
・リッジ回帰
・学習率
・LIME、SHAP
以上が大項目「機械学習の具体的な手法」の中の一つモデルの評価の内容でした。
モデル評価は「そのモデルがどれだけ正しい精度で予測できるか」を測る重要な要素です。
実務でも利用場面は多いでしょう。
今回でモデルの評価が終わり、大項目「機械学習の具体的な手法」の章がようやく終了です。
次回からは、大項目「ディープラーニングの概要」にはいっていきたいと思います。
覚える内容が多いですが、りけーこっとんも頑張ります!
ではまた~

続きは以下のページからどうぞ!










コメント