※本記事はアフィリエイト広告を含んでいます

どーも、りけーこっとんです。
「G検定取得してみたい!」「G検定の勉強始めた!」
このような、本格的にデータサイエンティストを目指そうとしている方はいないでしょうか?
また、こんな方はいませんか?
「なるべく費用をかけずにG検定取得したい」「G検定の内容について網羅的にまとまってるサイトが見たい」
今回はG検定の勉強をし始めた方、なるべく費用をかけたくない方にピッタリの内容。
りけーこっとんがG検定を勉強していく中で、新たに学んだ単語、内容をこの記事を通じてシェアしていこうと思います。
結構、文章量・知識量共に多くなっていくことが予想されます。
そこで、超重要項目と重要項目、覚えておきたい項目という形で表記の仕方を変えていきたいと思いますね。
早速G検定の中身について知りたいよ!という方は以下からどうぞ。

具体的にどうやって勉強したらいいの?
G検定ってどんな資格?
そんな方は以下の記事を参考にしてみてください。
なお、りけーこっとんは公式のシラバスを参考に勉強を進めています。
そこで主な勉強法としては
分からない単語出現 ⇒ web検索や参考書を通じて理解 ⇒ 暗記する
この流れです。
※この記事は合格を保証するものではありません
大項目「機械学習の具体的な手法」
G検定のシラバスを見てみると、試験内容が「大項目」「中項目」「学習項目」「詳細キーワード」と別れています。
本記事は「大項目」の「機械学習の具体的な手法」の内容。
その中でも「教師あり学習」というところに焦点を当ててキーワードを解説していきます。
G検定の大項目には以下の8つがあります。
・人工知能とは
・人工知能をめぐる動向
・人工知能分野の問題
・機械学習の具体的な手法
・ディープラーニングの概要
・ディープラーニングの手法
・ディープラーニングの社会実装に向けて
・数理統計
とくに太字にした「機械学習とディープラーニングの手法」が多めに出るようです。
本記事の範囲は、合格に向けては必須の基礎知識になります。
G検定のメインパートの一つなので、高得点を狙うに越したことはありません。
これから先の機械学習の理解を深めるために、そしてG検定合格するために、しっかり押さえておきましょう。
教師あり学習に関する内容が多くなってしまったので、記事を複数回に分割してお届けしようと思いますね。
教師あり学習の概要
教師あり学習とは教師データ(正解データ)に、学習の結果を近づけようとする機械学習の手法。
教師データ(正解データ)とは予め人間が用意したデータで、データの通りに機械が予測できれば正解、そうでなければ不正解となるデータのことです。
例えば犬と猫の画像があったとしましょう。
人間が用意した犬と猫の画像は「教師データ」です。
機械が画像に何が写っているかを予測した結果、犬を犬、猫を猫と出せるようにしたいのが、教師あり学習。
全体的な構成は以下の画像の通り。
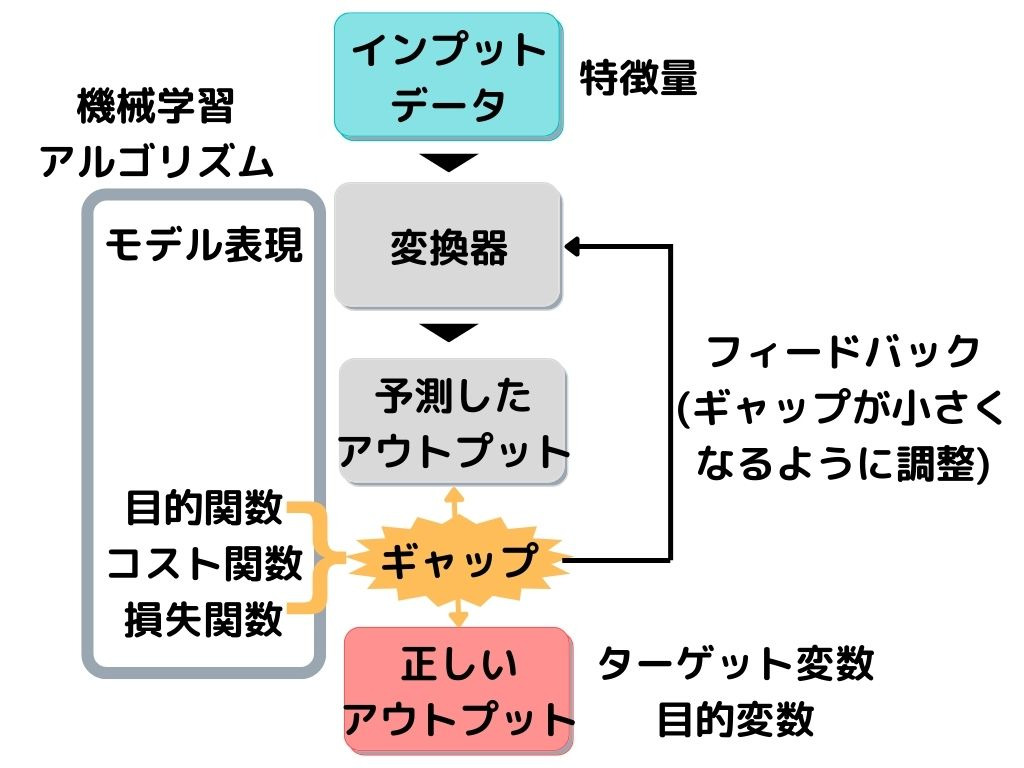
教師データは上の図で言うと「正しいアウトプット」に相当します。
専門用語だと「ターゲット変数」「目的変数」なんて言ったりもしますね。
変換器が「予測したアウトプット」と「正しいアウトプット」のギャップ(誤差)を埋めるために、何回も調整(学習)するのが、教師あり学習です。
これから出てくる手法は全て「変換器」の部分。
専門用語では変換器を「モデル表現」、ギャップや誤差を「目的関数・コスト関数・損失関数」なんても言います。
このモデル表現や目的関数を合わせて「機械学習アルゴリズム」と言ったりもしますね。
そして変換器に入力するデータが「特徴量」と言われます。
りけーこっとんは、よく目的関数と目的変数がごっちゃになります。
疑似相関
疑似相関とは対象の2つの変数同士に本当は相関関係が無いのに、見えない要因(潜伏変数)によって相関関係があるように見えてしまうこと。
例えば「昨日の食事量」と「体重」には相関があるように見えるかもしれません。
でも「昨日食べすぎたから、太った」ということは本当にあるのでしょうか。
「生活習慣で食べすぎているから、太っている」の方がしっくりきますよね。
この例では生活習慣での食事量、つまり「毎日の平均食事量」が見えない要因(潜伏変数)になっていたわけです。
問題の分類
教師あり学習を行うときに、解決したい問題を以下の二種類に分けることができます。
・分類問題
・回帰問題
それぞれどういう問題なのか、見ていきましょう。
分類問題
分類問題とは、出力が有限個の離散カテゴリである問題のこと。
離散カテゴリというのは「国・都道府県・人名・5段階評価」といった、数字が飛び飛びになっている種類のデータのことです。
例えば
「成績が一番高い人の予測」
「人口増加率が高い都道府県の予測」
などは、出力(出る結果)が「人の名前」や「都道府県名」ですよね。
これらは分類問題と呼ばれます。
さらに「成績が高いのはAくんBくん、どちらか」といった、出力が二つに限られる問題を2クラス問題
「このクラス内で成績が高いのは誰か」といった、出力が何個もある問題を多クラス問題と言います。
回帰問題
回帰問題とは、出力値が連続値である問題のこと。
こちらの方がイメージはしやすいかもしれません。
例えば
「1年後の身長の予測」
「とある病気にかかるのは何%か」
みたいな問題ですね。
身長や%は飛び飛びの値(離散カテゴリ)にはならず、小数点以下までの数字もあり得ます。
そのため、例のような問題は回帰問題です。
回帰分析
回帰分析とは、ある変数xとそれに相関のある連続値yの値を数式で表し、予測・説明すること。
変数には色々なものが入ります。
例えば「身長と体重の関係」を知りたければ、「身長」「体重」が変数となりますね。
よく以下の画像のようなイメージで表されます。
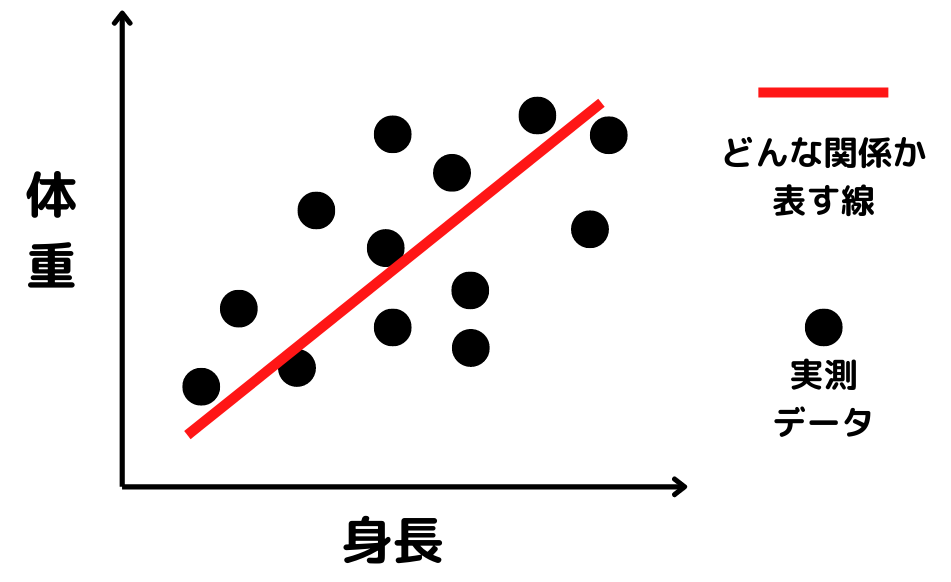
まず図の赤線の式を求めます。
式で書けると、「身長」「体重」にどんな関係があるのか説明できるようになるんですね。
さらに、未知のデータが来ても「身長」「体重」のどちらかが分かれば、もう片方は求められるという「予測」もできるようになります。
この一連の流れで、変数同士の関係や予測をする分析を回帰分析と呼びます。
単回帰分析
単回帰分析とは、一つの説明変数(特徴量)で回帰分析を行うこと。
上記の「身長と体重の関係」みたいな感じですね。
「身長」という一つの説明変数から「体重」を説明、予測しています。
重回帰分析
重回帰分析とは、2つ以上の説明変数(特徴量)で回帰分析を行うこと。
単回帰分析なんて現実問題ほぼ無くない?
と思った方は鋭いですね。
実際、学習モデルはほとんど重回帰分析です。
例えば「売上」を「立地」「商品数」「清潔さ」という説明変数で説明、予測するというような感じ。
難しそうな言葉ですが、例を挙げてみると分かりますね。
では次からは教師あり学習の「モデル表現」の種類を見ていきます。

線形回帰
線形回帰とは、説明変数と目的変数の間に線形の関係があると仮定した回帰分析。
ついさっき示した「身長と体重の関係」の例のようなものです。
線形の関係というのは一直線の線を引ける関係のこと。
曲がった線でしか関係を表せないときは、線形の関係とは言えません。
最小二乗法
最小二乗法とは、残差二乗和が最小になるような直線を探す方法。
簡単に言うと、全てのデータからの距離が一番近くなるような線を引こう!
ということです。
残差二乗和はイメージにするとこんな感じ。
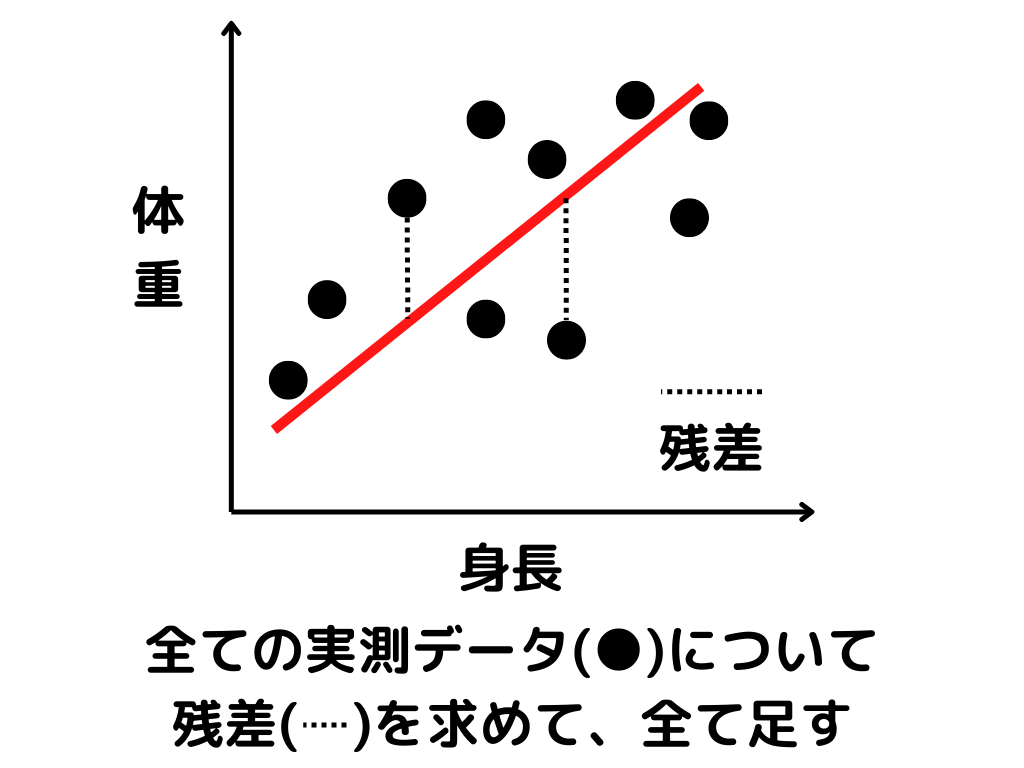
つまり、図で言うと
式は以下のような感じです。

決定木
決定木とは、データを分類する基準を定めた木のこと。
決定木を作り、どの特徴量・値を元にすれば上手く分けれるかを学習するモデル表現のことですね。
グラフを分けていくイメージで図示すると以下のような感じ。
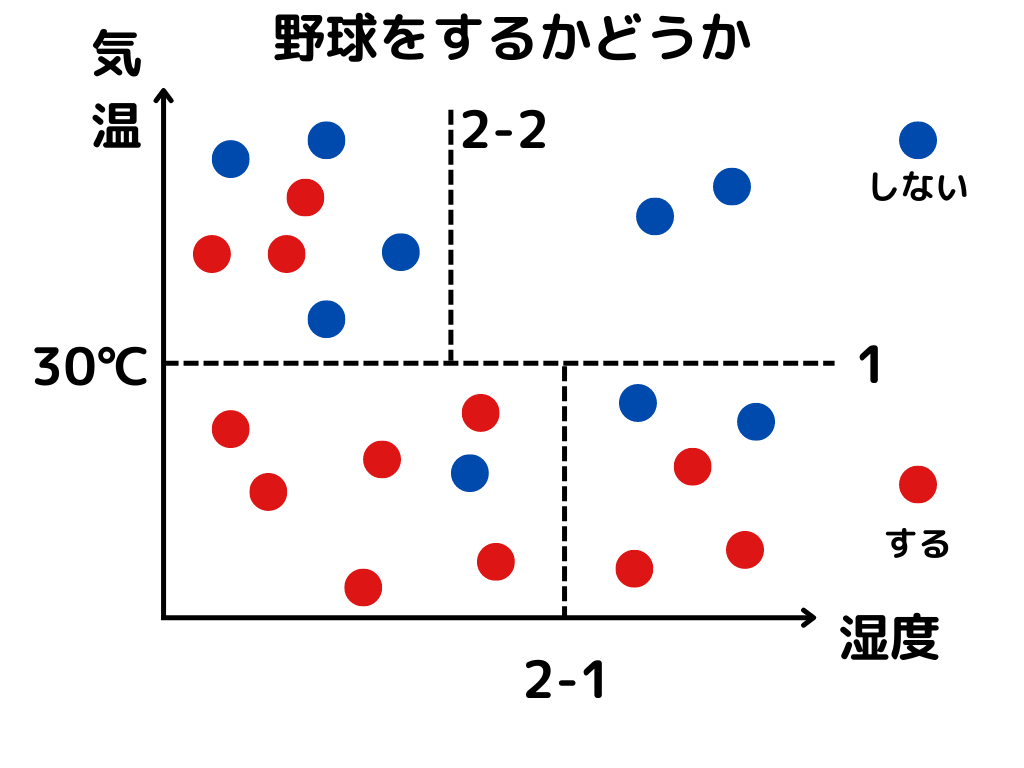
木のような図にすると以下のような感じ。
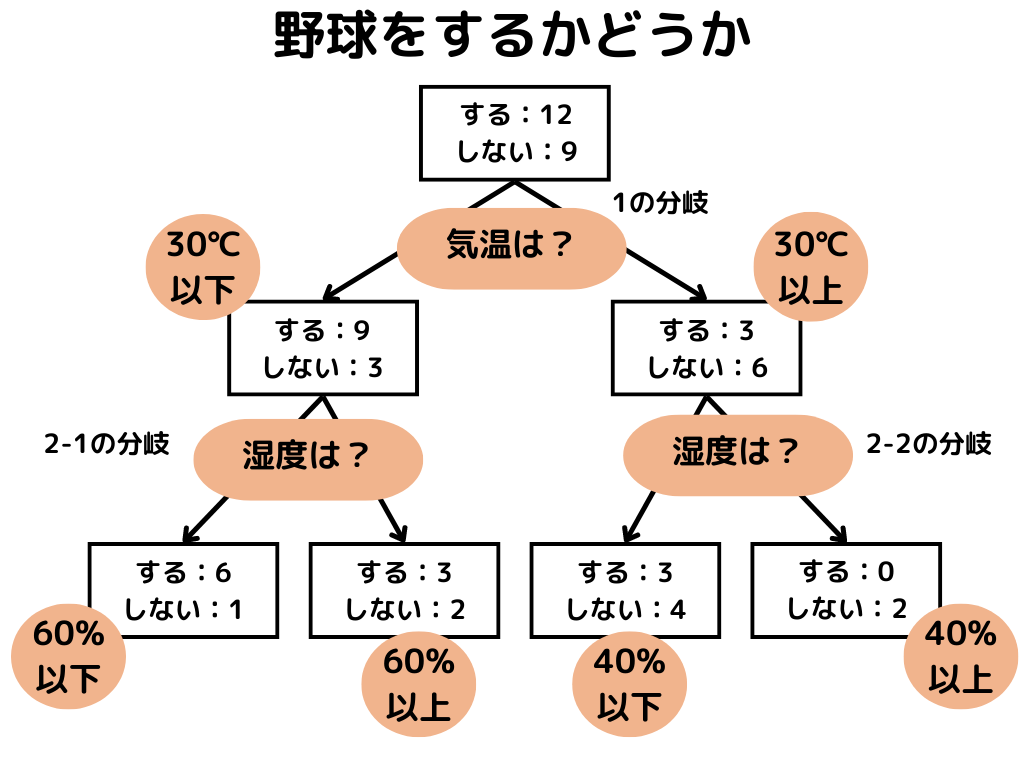
分類木
ところで、教師あり学習には問題の種類として「分類問題」と「回帰問題」の2つがあることを、前の章で述べました。
決定木は、そのどちらの問題に使うかによって、名前が変わります。
分類木とは、分類問題において用いられる決定木のこと。
回帰木
同じく「回帰問題」に対して使われる決定木にも名前があります。
説明が重複しますが、回帰木とは、回帰問題において用いられる決定木のこと。
ジニ係数
ジニ係数とは、決定木で区切った部屋の中の純度を測定する指標のこと。
教師あり学習の目的関数として用います。
ジニ係数は次の式で与えられます。
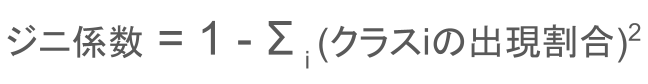
クラスiの出現確率というのは、区切った部屋の中で1つのクラス(区分け)が、出てくる割合のことです。
先ほどの図を例にすると、点線で区切られた小部屋の中で計算ができますね。

例えば左上の「野球をする人」のジニ係数は、1 – (3/7)**2 = 0.816。
右上の「野球をしない人」は 1 – 1 = 0 です。
つまり、ジニ係数は値が小さいと純度が高いという意味。
そのため、学習ではジニ係数を小さくするように進めていくようです。
メリット・デメリット
メリットとしては以下の二点が挙げられます。
・解釈可能性が高い
・連続値の正規化が不要
デメリットとしては以下。
・過学習を起こしやすい
専門用語が多くなってしまいましたね。
それぞれ軽く説明したいと思います。
解釈可能性
解釈可能性というのは「なんでそういう結論に達したか」を機械のアルゴリズムを見て判断しやすいかどうか、ということです。
ディープラーニングとかになってくると、複雑すぎて「精度が高い結論は出たけど、機械の中でどういう計算をやったかは分からない」という状況になることも。
ディープラーニングなどは「解釈可能性が低い」と言えそうです。
正規化
正規化というのは、たくさんあるデータを1つの基準に沿って変換し、スケールを合わせること。
例えば身長と体重であれば単位を考えないと、それぞれ数字のスケールが変わってきますよね。
身長であれば「1.2 ~ 2.0(m)」、体重であれば「40 ~ 100(kg)」と言ったところでしょうか。
数字の桁が違いすぎるので、直接比較がしにくいんですね。
もっと比較したい要素が増えればなおさら。
1つの基準は代表的なものだと「平均0、標準偏差1の正規分布にする」があります。
興味のある方は調べてみてください。
過学習
過学習とは、訓練用のデータを学習しすぎて、訓練用のデータの誤差が小さくなりすぎること。
訓練用データだけの話なら良いのですが、本当にやりたいことは未知データが来たときの予測です。
訓練用のデータに合わせすぎてしまうと、未知データの予測精度がむしろ落ちるんですね。
そのため、過学習がなるべく起こらない工夫が重要です。
使いどころ
実際にどのような場面に使うかと言えば、以下のような状況でしょうか。
・気軽に使える
・データ、重要な特徴量の理解
まとめ
今回は大項目「機械学習の具体的な手法」の中の一つ教師あり学習についての解説でした。
教師あり学習の流れは重要なので、もう一度見ておきましょう。

そして本記事の重要機ワードは以下。
・分類問題、回帰問題
・回帰分析
・線形回帰
・決定木
以上が大項目「機械学習の具体的な手法」の中の一つ教師あり学習の内容でした。
教師あり学習の手法は他にもあります。
なので、次回は他の教師あり学習の手法について解説させて頂きます。
覚える内容が多いですが、りけーこっとんも頑張ります!
ではまた~

続きは以下のページからどうぞ!










コメント