※本記事はアフィリエイト広告を含んでいます

どーも、りけーこっとんです。
「G検定取得してみたい!」「G検定の勉強始めた!」
このような、本格的にデータサイエンティストを目指そうとしている方はいないでしょうか?
また、こんな方はいませんか?
「なるべく費用をかけずにG検定取得したい」「G検定の内容について網羅的にまとまってるサイトが見たい」
今回はG検定の勉強をし始めた方、なるべく費用をかけたくない方にピッタリの内容。
りけーこっとんがG検定を勉強していく中で、新たに学んだ単語、内容をこの記事を通じてシェアしていこうと思います。
結構、文章量・知識量共に多くなっていくことが予想されます。
そこで、超重要項目と重要項目、覚えておきたい項目という形で表記の仕方を変えていきたいと思いますね。
早速G検定の中身について知りたいよ!という方は以下からどうぞ。

具体的にどうやって勉強したらいいの?
G検定ってどんな資格?
そんな方は以下の記事を参考にしてみてください。
なお、りけーこっとんは公式のシラバスを参考に勉強を進めています。
そこで主な勉強法としては
分からない単語出現 ⇒ web検索や参考書を通じて理解 ⇒ 暗記する
この流れです。
※この記事は合格を保証するものではありません
大項目「機械学習の具体的な手法」
G検定のシラバスを見てみると、試験内容が「大項目」「中項目」「学習項目」「詳細キーワード」と別れています。
本記事は「大項目」の「機械学習の具体的な手法」の内容。
その中でも「教師なし学習」というところに焦点を当ててキーワードを解説していきます。
G検定の大項目には以下の8つがあります。
・人工知能とは
・人工知能をめぐる動向
・人工知能分野の問題
・機械学習の具体的な手法
・ディープラーニングの概要
・ディープラーニングの手法
・ディープラーニングの社会実装に向けて
・数理統計
とくに太字にした「機械学習とディープラーニングの手法」が多めに出るようです。
本記事の範囲は、合格に向けては必須の基礎知識になります。
これから先の機械学習の理解を深めるために、そしてG検定合格するために、しっかり押さえておきましょう。
教師なし学習に関する内容が多くなってしまったので、記事を複数回に分割してお届けしようと思いますね。
教師なし学習の概要
教師なし学習とは、どういう特徴や傾向があるか分からないデータに傾向を見出したり、似たデータをまとめたりする機械学習の手法。
教師あり学習とは異なり、その名の通り「教師データ」がありません。
なので、教師なし学習で得られた結果を解釈することは、分析者などの人間が行います。
教師あり学習と教師なし学習の違いは以下の画像の通り。
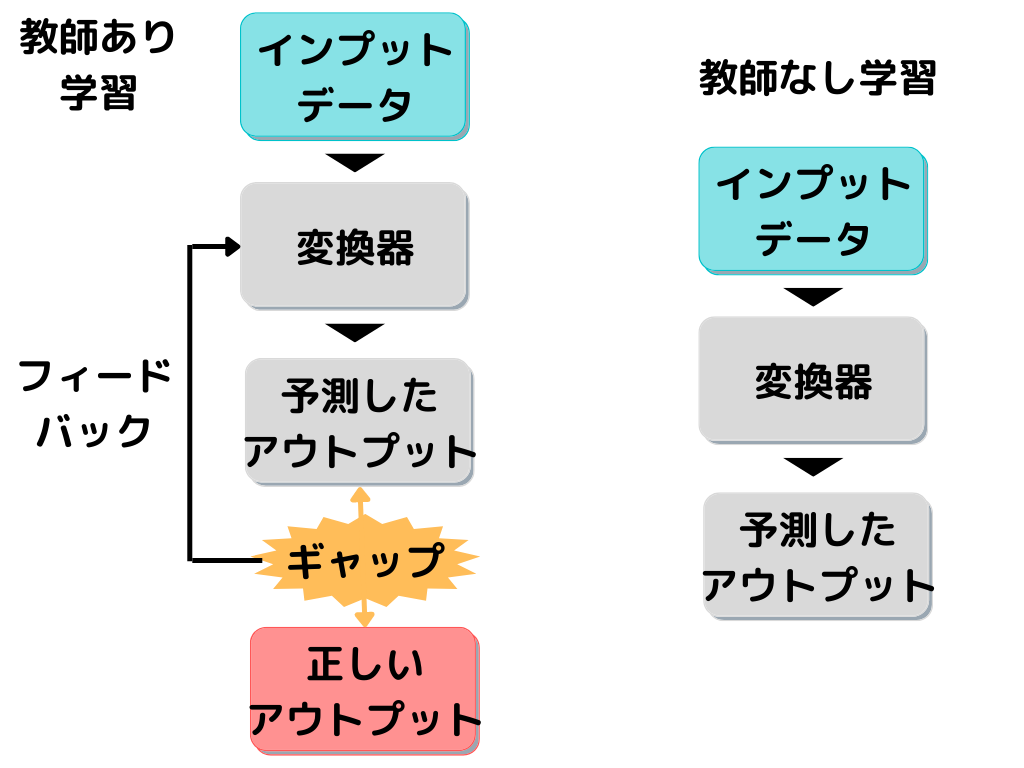
「正しいアウトプット」がないので、教師データがない、つまり「教師なし学習」というわけです。
さらに教師なし学習のイメージはこんな感じ。
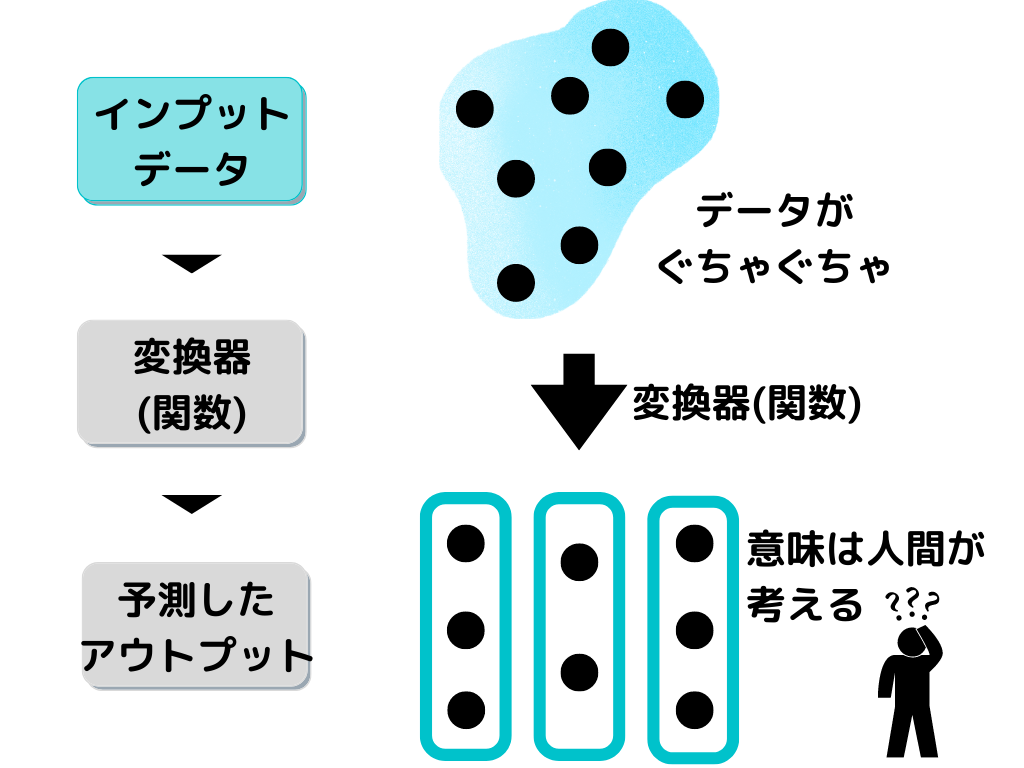
図のように、元々のデータには規則性がなく、ぐちゃぐちゃの状態です。
そのデータに「教師なし学習」を行うことで、どういう規則性があるのか、パターンを見出します。
「教師なし学習」が見つけるのは「パターン化に必要だった関数(変換器)」です。
元データから見出したパターンの解釈を、機械はできません。
規則的にデータをパターン化したら、そこから先は人間の仕事。
規則性から何が言えるのかを考察することで、ビジネスに活かすことができますよね。
今回は教師なし学習の得意とする「クラスタリング・クラスタ分析」「トピックモデル」「レコメンデーション」の分野に絞って解説していきたいと思います。
クラスタリング・クラスタ分析
クラスタリング・クラスタ分析とは、データを似たもの同士で分類すること。
データ同士の距離が近かったり、似た傾向があるものを1つにまとめるんです。
この1つにまとめた塊を「クラスタ」といいます。
注意したいのは、似たデータ同士をまとめるだけで、まとめたデータに意味を見出すのは人間ということ。
「教師なし学習」と言われるわけですね。
クラスタリングのやり方はいろいろあるのですが、大きくは2つ。
・階層的クラスタリング
・非階層的クラスタリング
まずは、非階層的クラスタリングの代表例から見ていきましょう。
k-means法
k-means法は以下のような手順で進みます。
1.k個のシードをおく(データを何個に分けるか自分で決める)
2.各サンプルを最も近いシードと同じクラスタに分ける
3.クラスタ毎に重心を求め、それを新たなシードとする
4.重心が移動しなくなるまで2.3を繰り返す
最初にk個のシード(クラスタ分けの基準となる点のこと)をおくことで、データを何分割にするか決めます。
この「最初にデータを何分割するか」を決めるのは分析者自身であり、非常に重要です。
k-means法は進める過程で、クラスタの数が変わりません。
なので「非階層的クラスタリング」に分類されますね。
メリットは
・計算が速い
・シンプルで実装しやすい
デメリットは
・事前にkを決める必要がある
・最初のシードの置き方で分類結果、計算時間が変わる
最初の置き方が重要なのに、その判断の仕方が分からないよ!
という方には、以下の2つの便利な手法があるんです。
・エルボー法(Elbow Method)
・シルエットプロット
これらを使うことで、最適なクラスタ数を求めることができます。
エルボー法(Elbow Method)
エルボー法(Elbow Method)とは、最適なクラスタ数を求める1つの手法。
具体的には以下の手順で進みます。
1.WCSS(Within Cluster Sum of Square)を求める
2.横軸/k(クラスタ数)、縦軸/WCSSのグラフを作る
3.WCSSがあまり下がらないkを求める
WCSSとは、重心から各データまでの距離の二乗の合計のこと。
線形回帰での残差二乗和みたいなものでしょうか。
この方法でグラフを作ると以下のような感じになります。
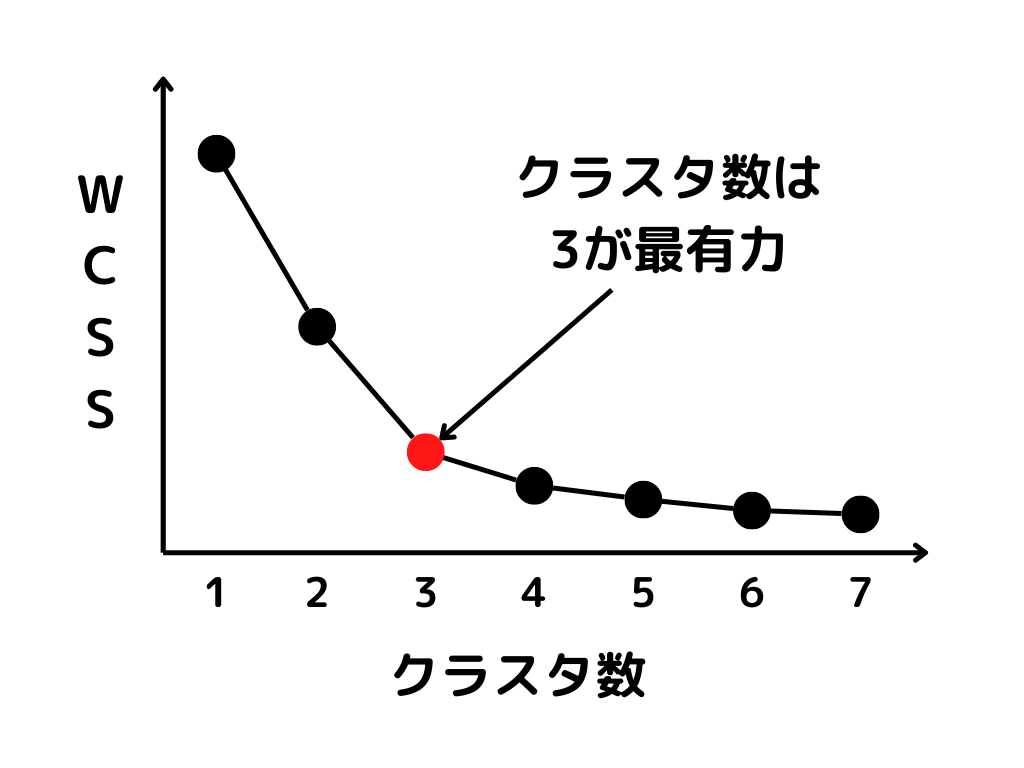
途中までは、各データまでの距離が減りやすいのですが、あるクラスタ数を超えるとあまり変化しなくなっていますよね。
あまり変化しなくなったクラスタ数を取ることで、ある程度最適なクラスタ数を求めることができます。
このグラフの形が「肘」のように見えることから、エルボー法と言われるようです。
シルエットプロット
シルエットプロットとは、最適なクラスタ数を求める1つの手法。
具体的には以下の手順で進みます。
1.以下の式より、全データのシルエットスコアを求める
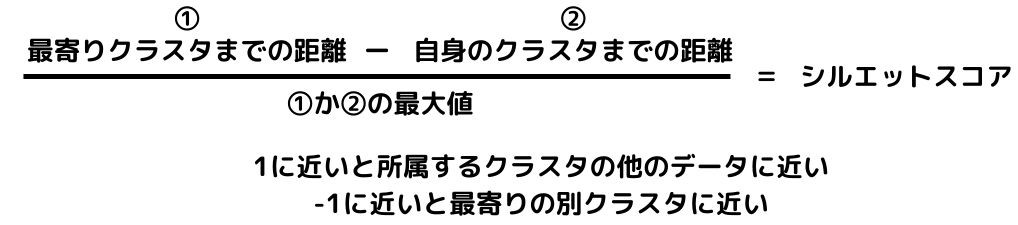
2.縦軸にクラスタ毎のデータ、横軸にシルエットスコアを取る(シルエットスコアが大きい順に上から並べる)
このグラフをシルエットプロットといいます。
クラスタ数が少なすぎるとこんな形。(左がシルエットプロット、右が元データ)

赤い点線が平均のシルエットスコアです。
黒いグラフの面積が多く、平均を超えていないデータしかないことが分かりますね。
これは、黒のクラスタが広がりすぎてしまっていることを示しています。
多すぎると以下の様な感じ。
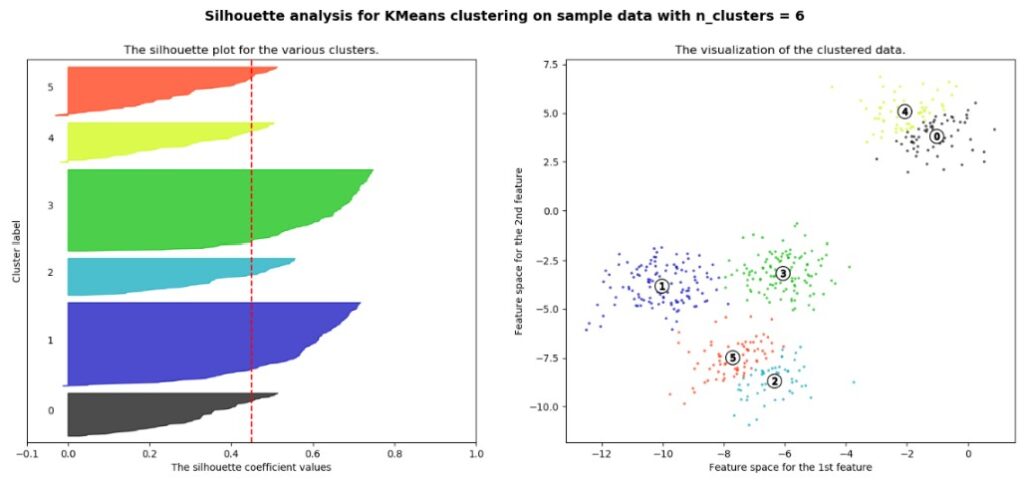
クラスタを分割しすぎると、三角形のグラフが目立ちますね。
この形が見えてきたら、クラスタ数は多すぎるということになります。
一番最適なクラスタ数になると、以下の様な感じになりますね。
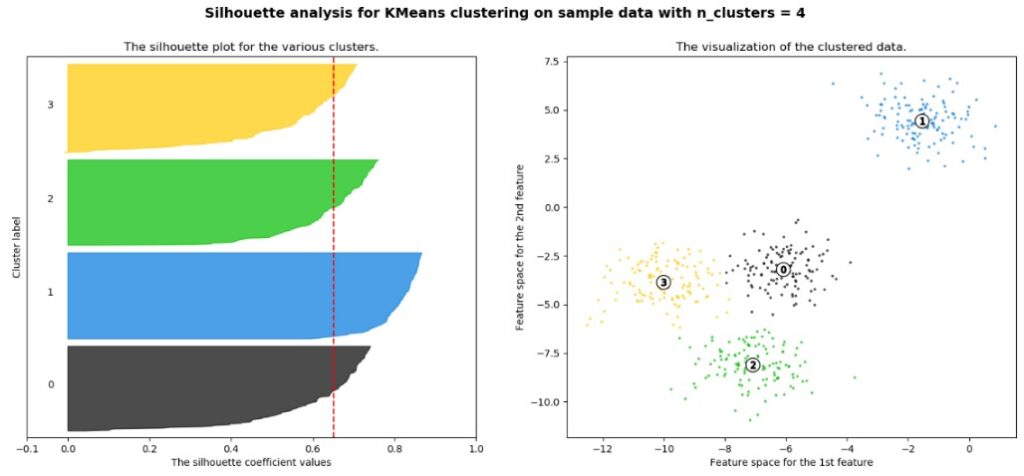
このようにシルエットプロットの形を見ることで、最適なクラスタ数を考える方法です。
階層的クラスタリング
階層的クラスタリングとは、段階的にクラスタリングを進める方法のこと。
先ほどまでのk-means法は、最初にクラスタ数を決めてしまいましたよね。
最初に決めてしまうのではなく、
最初は2つに分けてみる→3つに分けてみる…
といった形でクラスタリングを進めていきます。
事前にクラスタ数を決める必要が無いので、データが何分割されるか分からないときなどに有効です。
デンドログラム(樹形図)
デンドログラム(樹形図)とは、樹形図を書きながら段階的にクラスタリングを行う手法のこと。
実際に書いてみると以下のようになります。
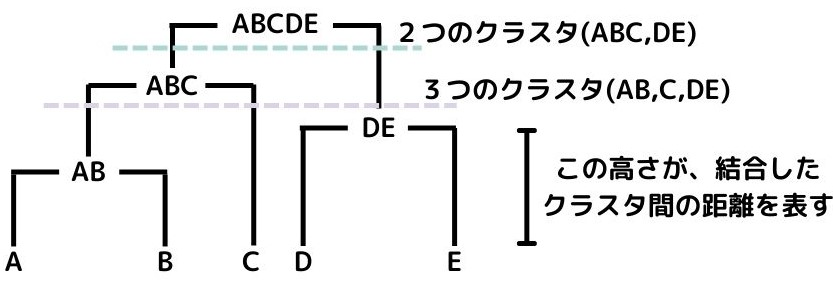
上から順に見ていくと、元データ(クラスタA~E)をまず、ABCとDEに分けています。
次の段階ではABCのクラスタをABとCに分けていますよね。
さらに「高さ」がクラスタの距離を示しているので、どれくらいクラスタ同士が近いのか、一目で分かります。
メリットとしては以下の通り。
・事前にクラスタ数を決める必要がない
・樹形図があるので可読性がある
デメリットは、以下の通り。
・計算量が多い
・ビッグデータは訳わかんなくなる
最短・長距離法
最短・長距離法とは、二つのクラスタで最も近い、または遠いデータ同士をクラスタ間の距離とする階層的クラスタリングの手法。
最短距離法のメリットとしては処理時間が短いことが挙げられます。
逆にデメリットとしては、分類感度が低いことです。
最長距離法のメリットとしては、処理時間が短い上に、分類感度が高いこと。
これは最短距離法よりも優れていそうな手法ですよね。
デメリットとしては、クラスタの規模が大きくなるとクラスタ同士が離れてしまう性質(拡散現象)を持つことです。
この拡散現象については、G検定では重要度は高くないと思います。
群平均法
群平均法とは、各クラスタ同士、全ての組み合わせのデータ間距離の平均をクラスタ間距離とする非階層的クラスタリングの手法。
分類感度が高く、拡散現象も起こしにくい手法です。
最短距離法・最長距離法の2つよりも優れていることから、よく使われるようです。
ウォード法
ウォード法とは、2クラスタを結合する前後での分散の増加量をクラスタ間距離とする非階層的クラスタリングの手法。
分散というのは、データのばらつき具合のことでした。
つまり、2つのクラスタを結合すると、データの量もばらつきも大きくなるので、分散が大きくなります。
結合した後に分散があまり増えなければ、その2つのクラスタの距離は近く、似ているということ。
ウォード法のメリットとしては、分類感度がすごく良いということです。
デメリットとしては最短・長距離や平均じゃなく分散を求めるので、計算量が多く、処理時間が長いことですね。

トピックモデル
トピックモデルとは、文書が複数の潜在的トピックから確率的に生成されると仮定し、トピックを見出すモデルのこと。
トピック毎に単語の出現頻度分布を想定することで、トピック間の類似性や意味を理解できる様になります。
これは、よく使われる手法である「潜在的ディリクレ配分法」を思い出すと、理解できると思います。
簡単に言ってしまえば「たくさんある文書(記事など)は、それぞれどういうトピックに分類できるのかな?」を考えられるモデルです。
レコメンデーション
レコメンデーションとは顧客の訪問履歴や購入履歴を元に、顧客に自動的に商品を勧めること。
Amazonや楽天にも「この商品を買った人はこんな商品も買っています」的な機能を見たことある人も多いのではないでしょうか。
この機能のもう少し詳細な部分(手法)が、G検定のシラバスに載っていたため、解説します。
手法としては大きく2つ。
・協調フィルタリング
・コンテンツベースフィルタリング
それぞれ見ていきましょう。
協調フィルタリング
協調フィルタリングとは、対象者がチェック・購入したデータから、パーソナライズされた商品を提示できるレコメンデーションの1手法。
一番想像しやすい手法ではないでしょうか。
対象者がチェック・購入したデータを「行動履歴」といったりもしますね。
対象者とそれ以外の購入・チェックデータを相関分析し、行動履歴を関連づけることで行えます。
コールドスタート問題
コールドスタート問題とは、協調フィルタリングの問題の一つ。
以下の様な問題が挙げられます。
・新規顧客はデータ数が乏しく、適切な推薦ができない
・商品の変化が激しいと十分なデータが得られる前に新商品が出て、意味が無くなってしまう。
つまり、元となる「行動履歴」のデータが少なすぎて、上手くオススメできないと言う問題のことですね。
コンテンツベースフィルタリング
コンテンツベースフィルタリングとは、商品の特徴ベクトルで類似度ソートしてレコメンドする方法。
つまりは、似た商品の特徴を持つ商品をオススメするということです。
行動履歴を元にはせず、あくまで商品の内容に注目して似た商品を勧めます。
例としては「新宿・和食」で検索すると関連するお店が出てくるイメージ。
このように、「レコメンド・レコメンデーション」といっても、複数の手法があることが分かりました。
まとめ
今回は大項目「機械学習の具体的な手法」の中の一つ教師なし学習についての解説、第二弾でした。
本記事の重要キーワードは以下。
・クラスタリング
・k-means法
・デンドログラム
・協調フィルタリング
・ウォード法
・トピックモデル
・コールドスタート問題
・コンテンツベースフィルタリング
以上が大項目「機械学習の具体的な手法」の中の一つ教師なし学習の内容でした。
これで「教師なし学習」は終了です。
次回からは「半教師あり学習」「強化学習」にはいっていきたいと思います
覚える内容が多いですが、りけーこっとんも頑張ります!
ではまた~

続きは以下のページからどうぞ!










コメント