※本記事はアフィリエイト広告を含んでいます

どーも、学生生活も残り半年を切って物思いにふけることが多くなっているりけーこっとんです。
皆さんは日々積み重ねていること、地道な努力を頑張っていることはありますか?
りけーこっとんは入社前に統計学の基礎だけでも固めておこうかな、と思ってます。
そこで今回は「データ分析のための統計学入門」のまとめの第二弾!
第二章の内容を分かりやすくまとめてみたいと思います。
前回からの続きですね。
第一弾はこちら。
「データ分析のための統計学入門」 とはアメリカのデータサイエンティストの方々が統計について、統計をどう実際の分析や現場に利用していくかを執筆したもの。
「アメリカの人が書いたって事は、英語…?読める気がしない…」
という方も日本語訳があるので大丈夫!(日本語無料版には、練習問題の解説が付いていません)
これから統計を学ぶ人たち、データサイエンティストを目指す人たちは、読んでおいて損はないと思います。
日本統計協会も「大学で初めて統計学を学ぶ学生、ビジネスでデータ分析をしている社会人のために
書かれた豊富で実践的な練習問題を含む最適な統計学入門書」というお墨付き。
何よりも魅力的なのは、無料公開という点!
統計学についてド素人な自分にとって、どの書籍を買ったら良いか分からなかったので、すごくありがたいです。
下のURLから、無料公開されているページに飛べます。
http://www.kunitomo-lab.sakura.ne.jp/2021-3-3Open(S).pdf
今回の記事は「読む前にさらっと概要を知りたい」という人向け。
より厳密な内容、詳しい内容は原文を読んで貰いたいと思うので、ここでは概略を絵を使ってさらっていきたいと思います。
では早速始めていきましょう。
第二章の概略
第二章は「統計データの記述」という題目。
文字通りデータの統計的分析について述べられています。
まずは結論からいきましょう。
ここでりけーこっとんが学んだ内容は以下の三つ。
・データの表し方(グラフの仕方)について
・カテゴリカルデータの表し方(グラフの仕方)について
・実際の現場で統計学がどう使われているのか
主にこの章では集めたデータをどう表すのか、ということに焦点を当てていました。
それぞれ詳しく見ていきましょう!
データの表し方(グラフの仕方)について
第一章では統計学が実際の現場でどのように使われているのかを見ていました。
第一章は既に記事にしてあるので、気になる方は以下の画像から。
第一章を端的にまとめるとこんな感じ。
・統計学の概要と応用例
・データの集め方
・実験のやり方
この第一章を踏まえて第二章ではデータを集めた後の話をしています。
りけーこっとんが印象に残ったのは、データの表し方の種類。
こんなにたくさんあるのかと思いましたね。
データの表し方としてあるのは以下のようなもの。
・散布図
・ドットプロット
・ヒストグラム
・箱ひげ図
・強度地図
それぞれがどのようなものか詳しく見ていきましょう!
散布図
散布図とは縦軸と横軸にそれぞれ、相関を見たい変数を入れ、一つ一つのデータを点で打っていくグラフの表し方です。
イメージとしてはこんな感じ。
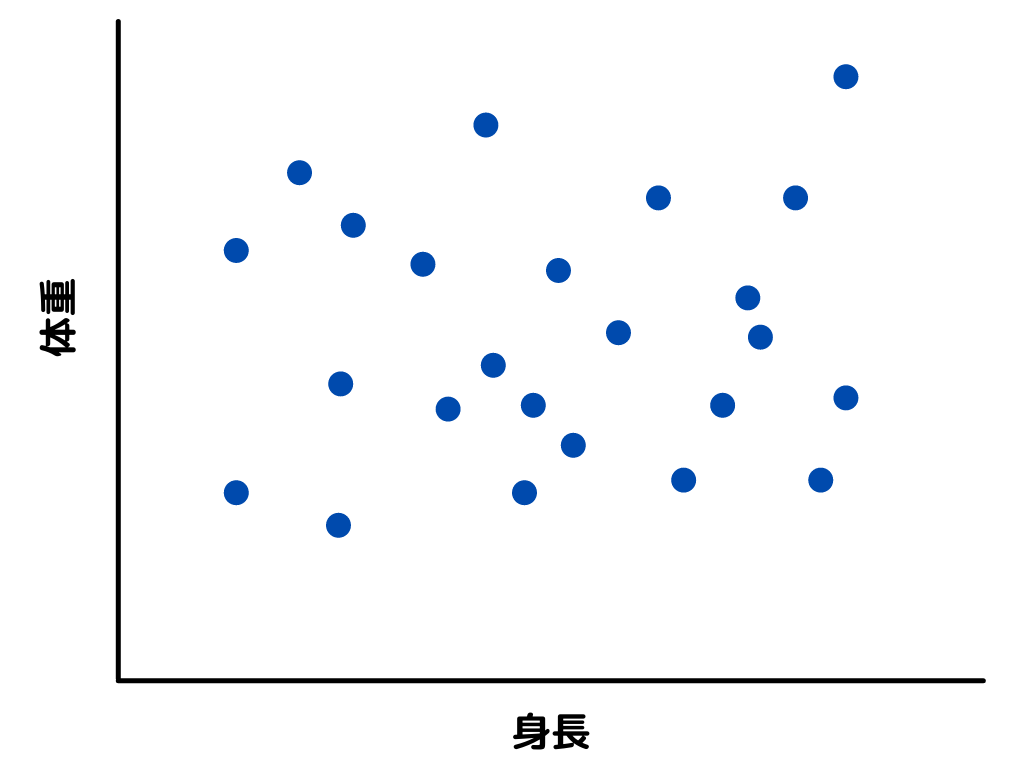
点の数を増やすと…
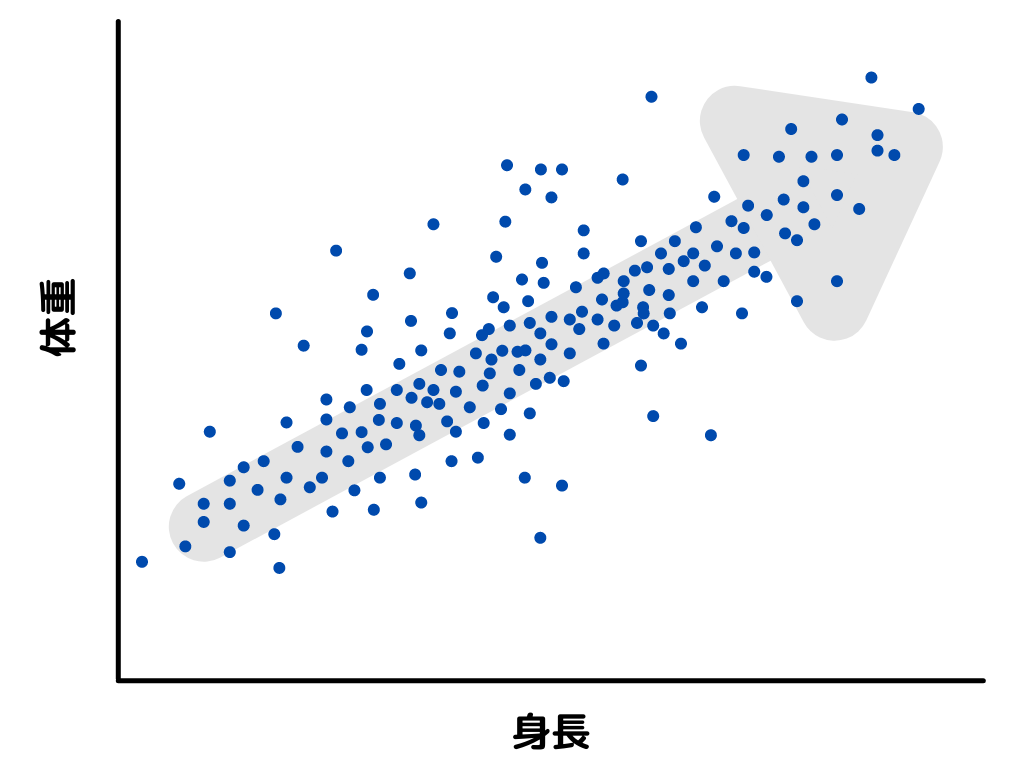
散布図はデータが、二つの軸に示した変数の中で、どのくらいの位置にいるのかを分かりやすくしてくれますね。
さらに二つの軸に示した変数に正の相関(片方の変数が大きくなればもう片方も大きくなる)があるのか、負の相関(片方の変数が小さくなればもう片方も小さくなる)があるのか、そのどちらでもないのかも示してくれます。
このグラフは見たことがあるという方も多いのではないでしょうか。
ドットプロット
ドットプロットとは一直線の上に、一つ一つのデータを点で打っていくデータの表し方です。
散布図が二変数のグラフだったのに対し、ドットプロットは一変数のグラフという感じですね。
イメージとしてはこんな感じ。
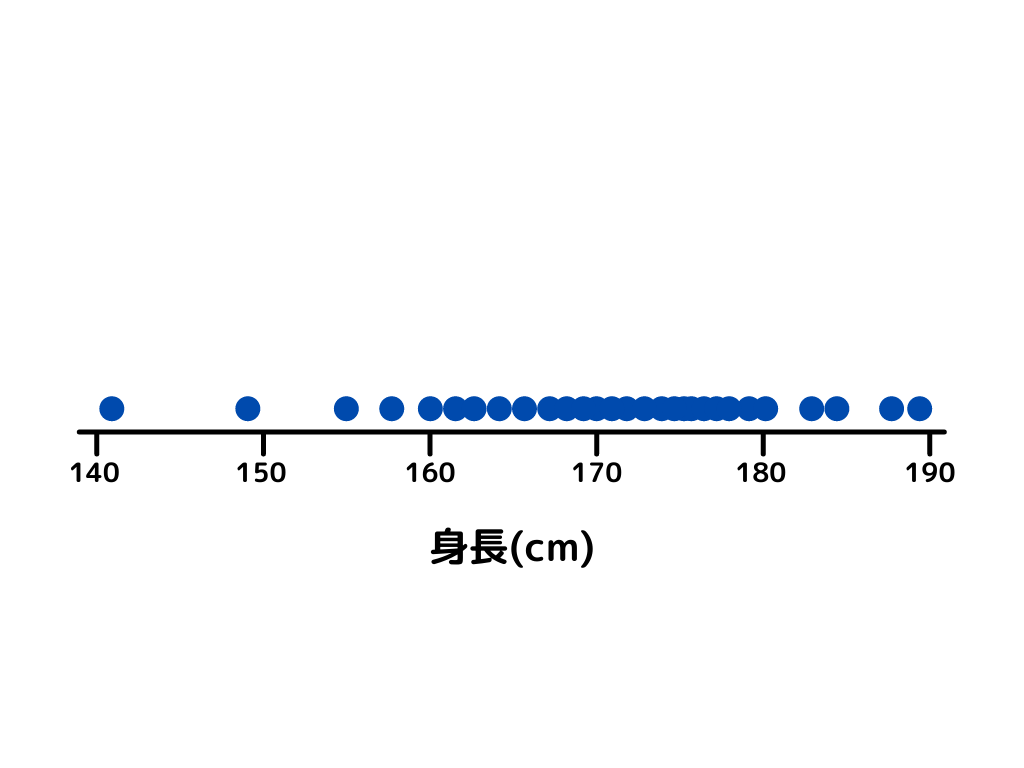
データ数が少なければ、この表し方が簡単そうですが、多くなるに連れて点が重なりすぎて分かりにくくなりそうですね。
そこで次のようなグラフがあります。
ヒストグラム
ヒストグラムとは片方の変数データの範囲を固定化して、その範囲に収まるデータ数を数えるというもの。
イメージとしてはこんな感じです。
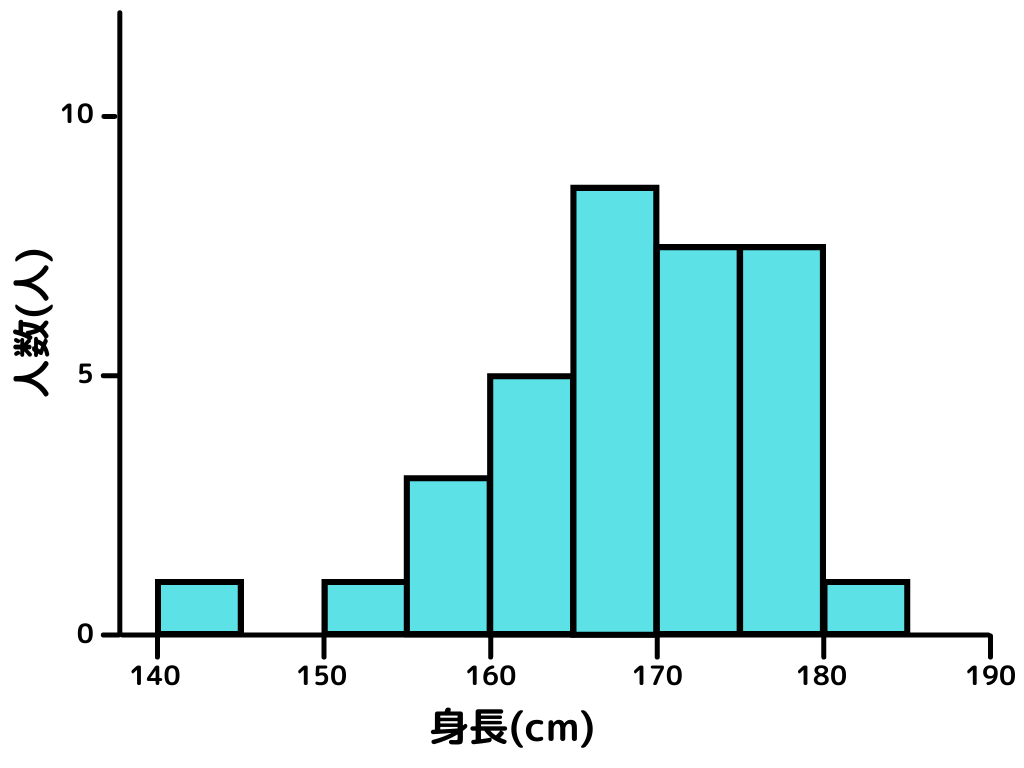
このグラフだと165~170 cmが一番多く、180 cm以上の人や150 cm以下の人は少ないということが分かりますよね。
このようにデータがどこに多いか、どのようなデータ分布になっているかを知ることができます。
データ分布の裾がどちらに伸びているかで、右(左)に歪んでいる、という表現も。
裾が右(左)に伸びていれば、グラフが右(左)裾が長い、右(左)に歪んでいる、といった言い方をするようです。
箱ひげ図
箱ひげ図とはデータ全体を”箱”と”ひげ”を使うことで、一つにまとめて表すことが出来るもの。
イメージとしてはこんな感じ。
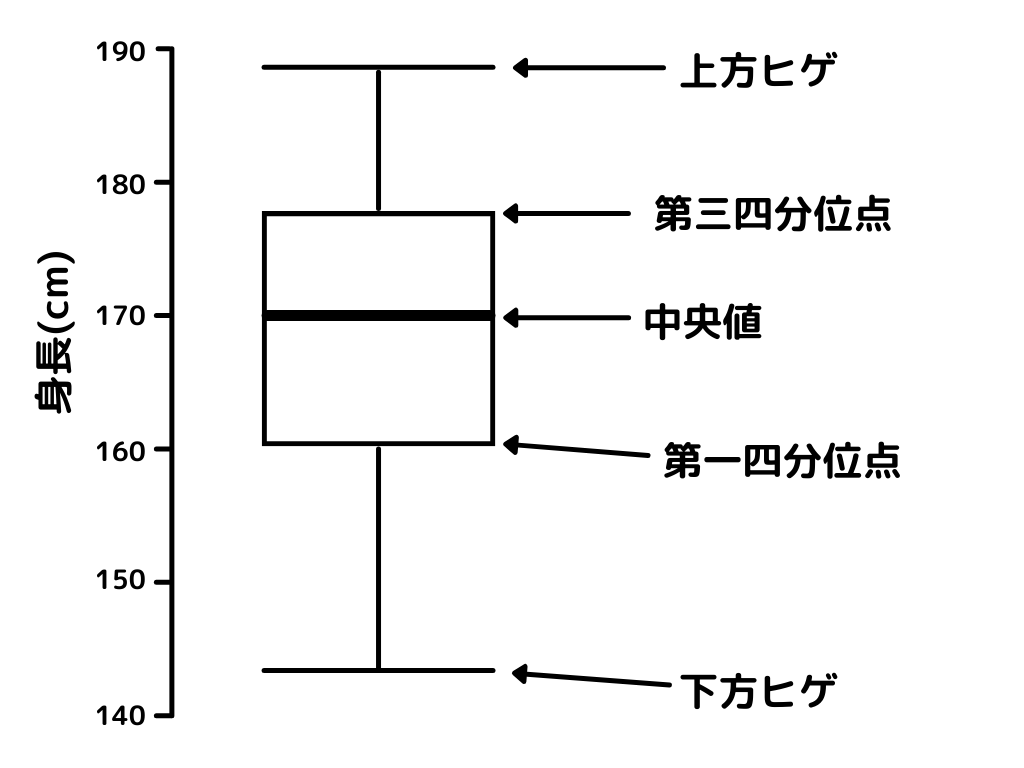
中央値とはデータの数を大きい方からも小さい方からも数えたときに、ちょうど真ん中に来るデータのこと。(ex データが10個あれば大きい方から(小さい方から)5個目と6個目のデータ値の平均、9個であれば5個目のデータ値)
第一四分位点とは、最小値と中央値のちょうど真ん中に来るデータ値のことです。
第三四分位点とは、最大値と中央値のちょうど真ん中に来るデータ値のこと。
上記三つはデータの個数を数えたときに真ん中の値であって、平均とは異なります。
このように大量のデータを一つの”箱”と”ひげ”で表せます。
強度地図
強度地図とは実際の地図に、色を利用してデータの数を表していくもの。
イメージとしてはこんな感じです。

このように、どの色になる程、データ値が高い(低い)ということが分かります。
これは地域毎のデータを表したいときによく使うようです。

カテゴリカルデータの表し方(グラフの仕方)について
次に学んだことがカテゴリカルデータの表し方についてです。
カテゴリカルデータを復習すると、数字で表さない(表せない)、名称などで分類される変数のことです。(第一章まとめ参照:ex 都道府県、国、人名など)
先ほどまでの表し方は、カテゴリカルデータを表せる種類もあるものの、基本的には数字データの変数を扱いやすいものになっています。
カテゴリカルデータを表しやすいやり方としては、以下のようなものがあります。
・分割表
・棒グラフ
・モザイクプロット
それぞれ見ていきましょう!
分割表
分割表とは、行と列それぞれにカテゴリカルデータを持つ変数を入れ、表にすることです。
イメージとしてはこんな感じ。(数値は目安として入れているもので、正しいものではありません)
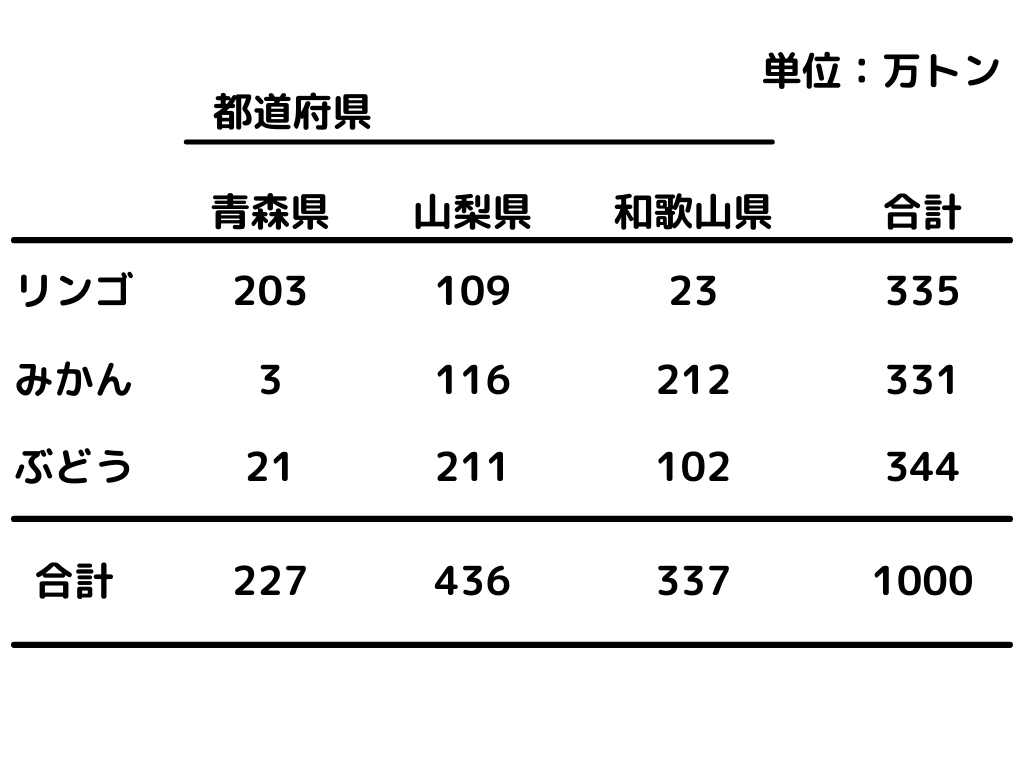
一般的に見る表ですね。
これを分割表と言うのは知りませんでしたw
この表し方は2変数同士の組み合わせ方で、どれだけのデータがあるかを知ることができます。
棒グラフ
棒グラフとは1つのカテゴリカル変数のデータ値を、それぞれ棒の高さで表現する表し方です。
これにも馴染みのある方は、多いのではないでしょうか。
イメージとしてはこんな感じ。
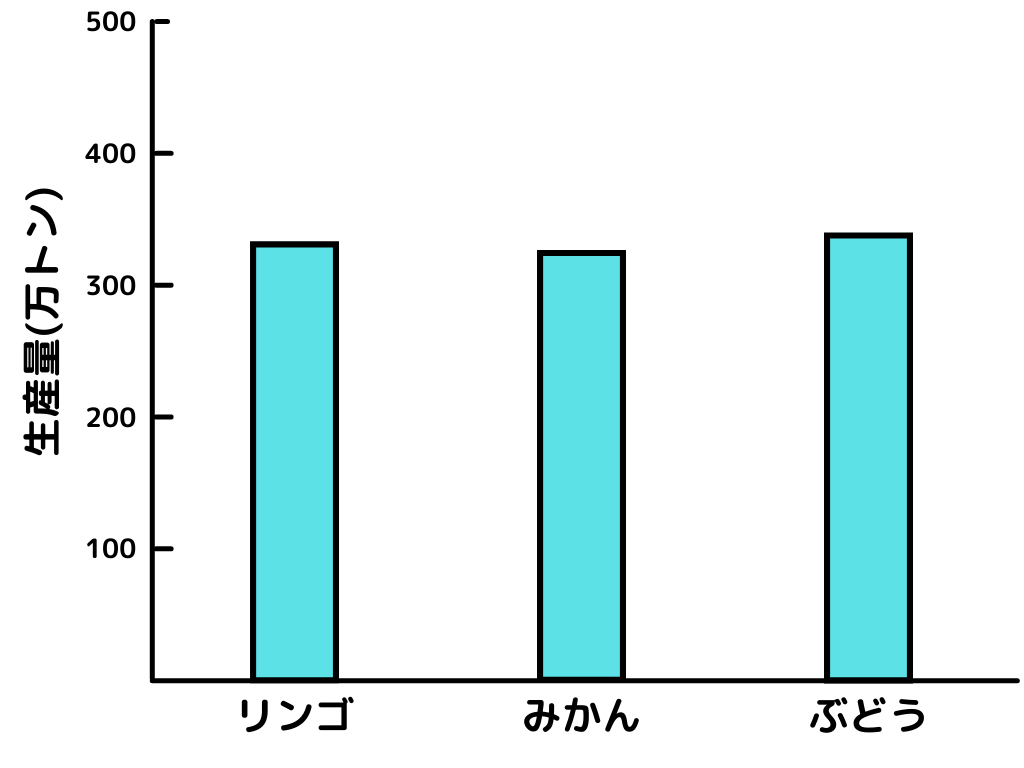
このように、どのカテゴリが多いか少ないか、変わらないのかを判断できます。
また、棒グラフには数種類あるのでそれもご紹介。
●積み重ね棒グラフ
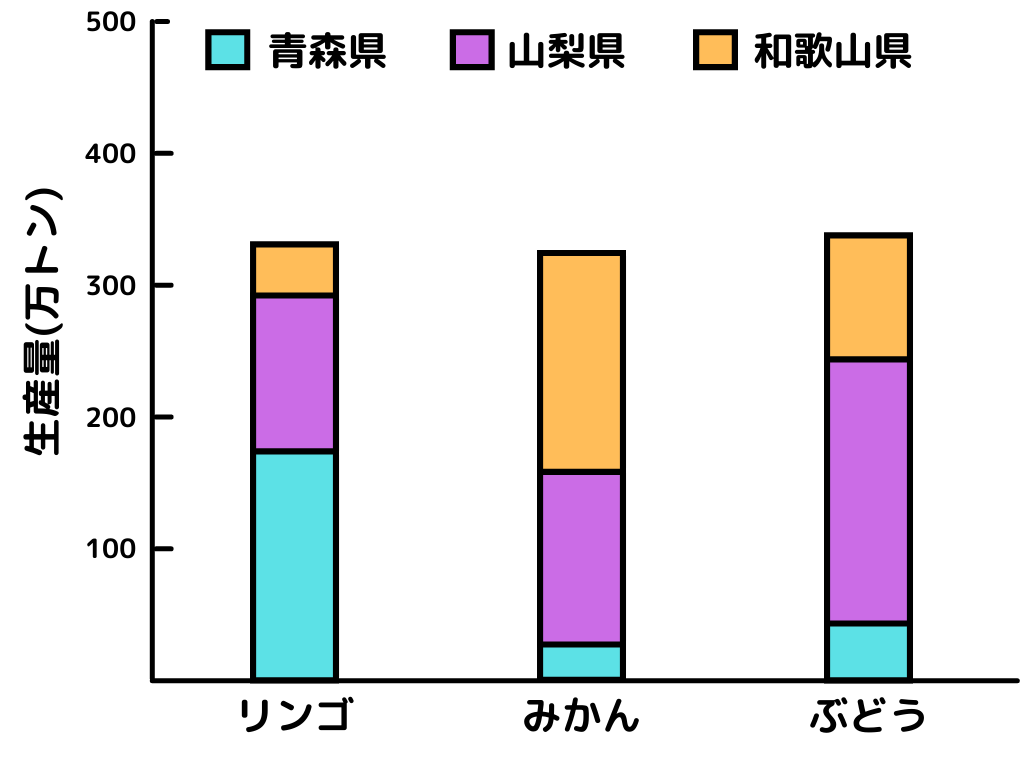
●平行棒グラフ
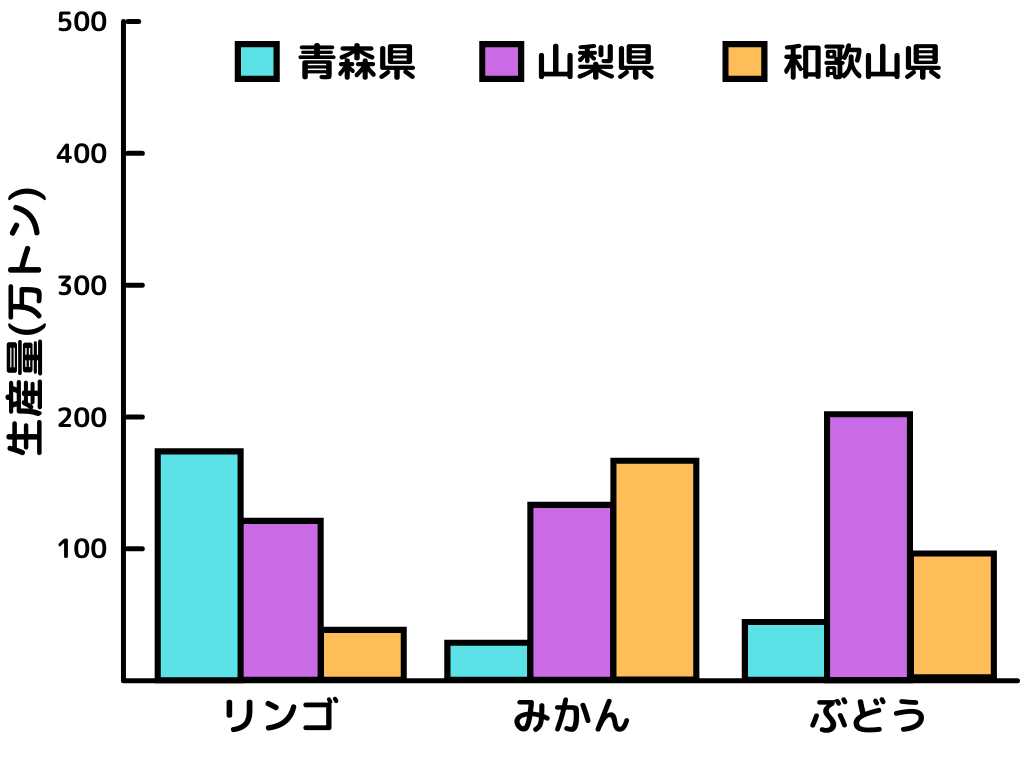
●標準化された棒グラフ
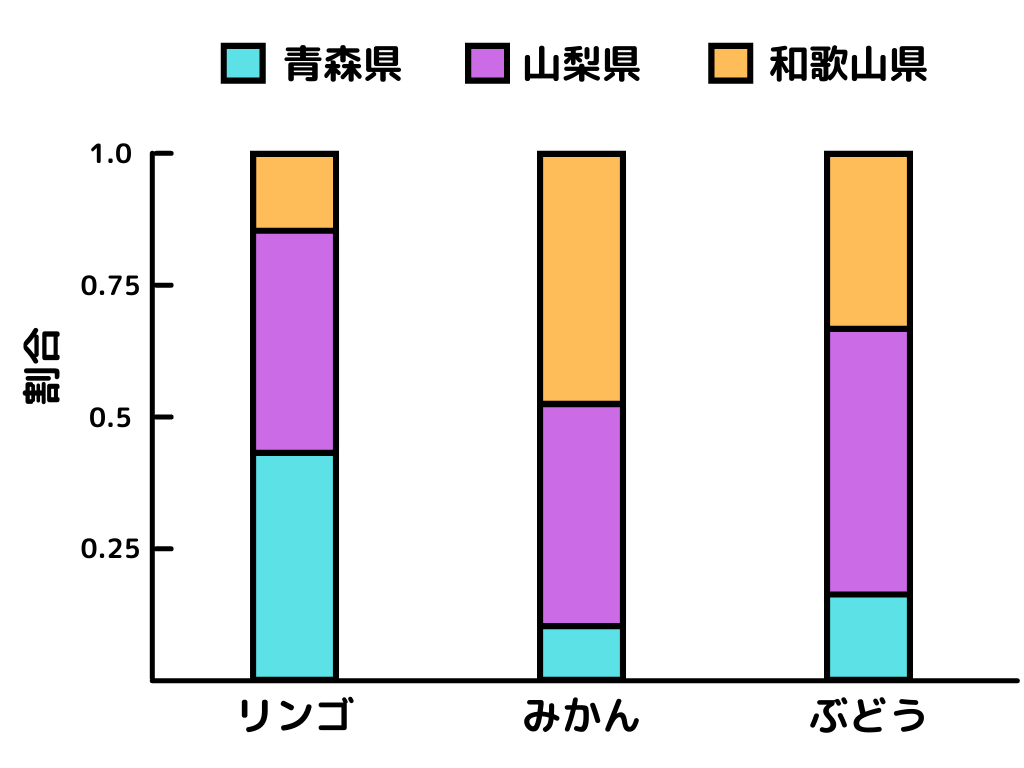
モザイクプロット
モザイクプロットとは、正方形をデータの大きさで区切った表し方。
イメージとしてはこんな感じ。
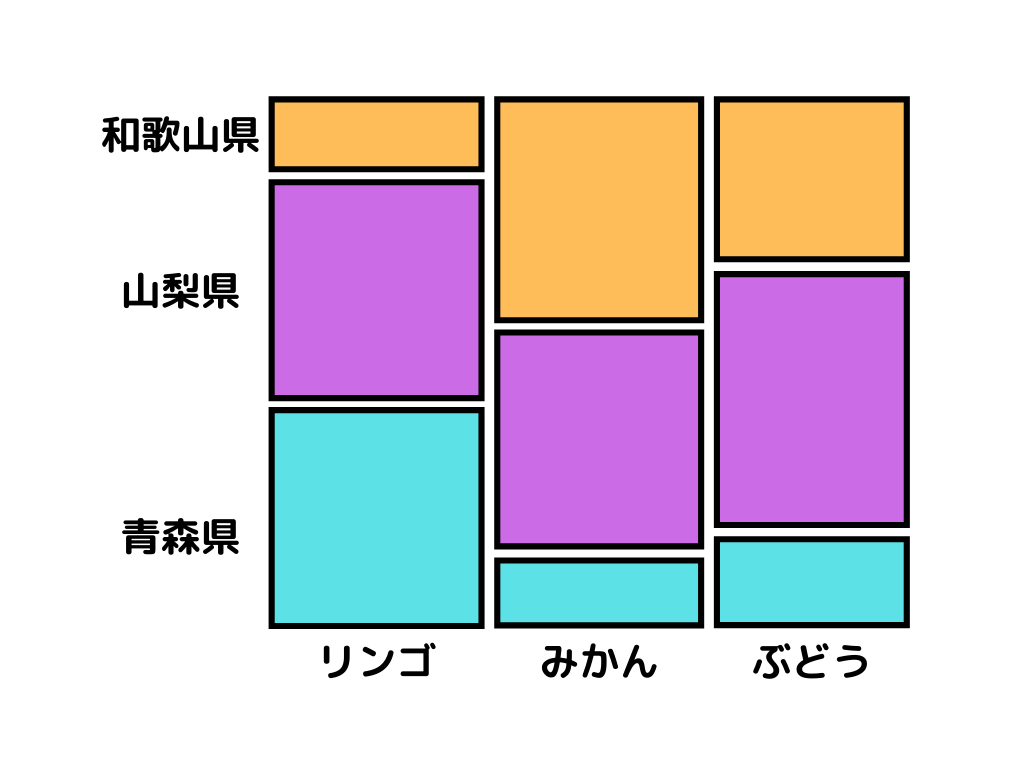
このように四角の大きさが大きいほど、データが大きいことが分かります。
ただ、他のデータと比べて多い・少ないという相対的な話になりがちと言うことだけ注意が必要ですね。
実際の現場で統計学がどう使われているのか
最後に学んだのは、統計学が実際の現場でどのように使われているのかです。
今回例として挙げられていたのはマラリアワクチンの有効性について。
効果があるとされている薬と偽薬(プラセボ)を投与し、その後マラリアに罹患させて感染したかどうかを見た実験です。
そこで得られた結果は、マラリアワクチンを接種した方が感染しないというもの。
しかし、ここで一つの疑問が浮かび上がります。
それは「この実験結果は本当に効果があると示しているのか、それとも誤差の範囲内なのか」ということ。
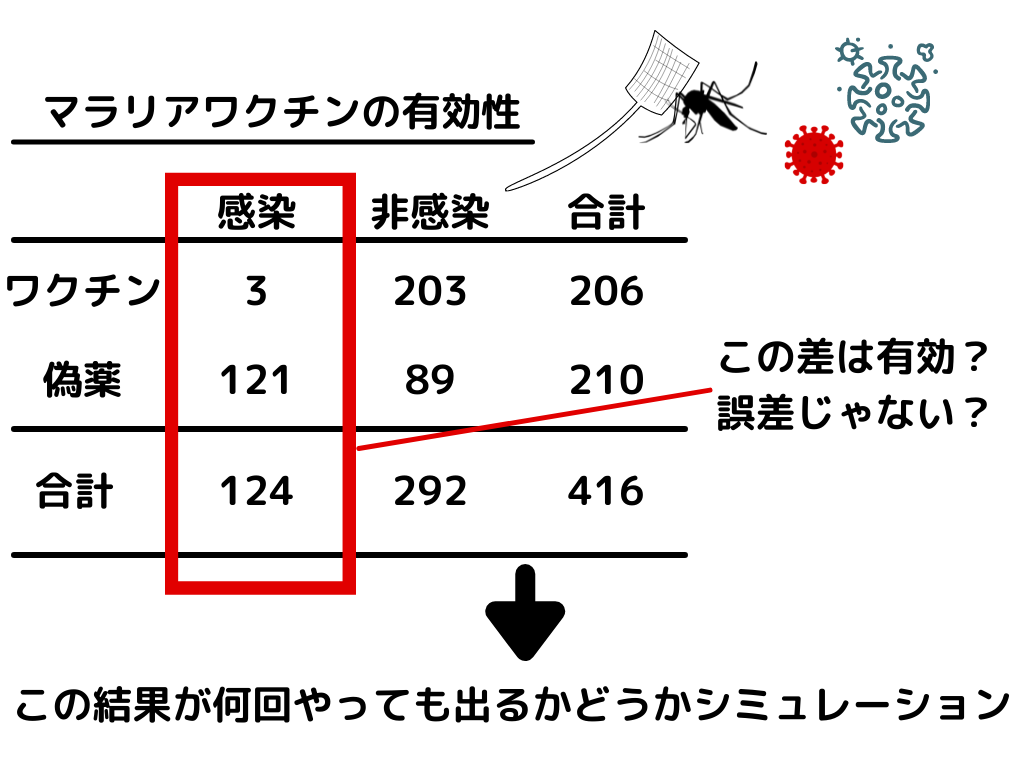
これを確かめるためにシミュレーション研究を行うようです。
シミュレーション研究とは実際に観察された結果がよく見られるのか、そうでないかを知るための研究のこと。
ここでのシミュレーション研究の状況想定は以下のようなもの。
1.ワクチンと偽薬摂取の被験者人数は固定
2.それぞれの被験者に決められた枚数の”感染”または”非感染”と書かれた紙(感染:11枚、非感染:9枚)をランダムに渡す
3.1と2を十分な回数繰り返す
これには主にプログラミングを用いることが多いようですね。
このように統計学は実際に実験を行った結果に対して、その結果は有意な差と言えるのか、誤差の範囲内なのかを知ることに使われるようです。
まとめ
今回の内容をまとめると以下の通りです。
・データの表し方には多数の種類があり、表したい変数の数・状況によって使い分ける
・統計学は得られた実験結果が有意な差と言えるのか、そうでないのかを判断するために用いられることがある
本記事は「データ分析のための統計学入門」のまとめの第二弾でした。
データサイエンティストになる身としては、統計の基礎中の基礎が「データ分析のための統計学入門」を読むことで、理解できている気がしますね。
統計学を全く学んでこなかったりけーこっとんでも、図が多用されながら分かりやすく解説されています。
初心者からデータサイエンティストになるよ!という方は「データ分析のための統計学入門」から勉強を開始することをオススメしますよ。
より良いキャリア形成のために、これからも学習を進めていきます!
それではまた~

続きの第三章は以下のページからどうぞ!








コメント