※本記事はアフィリエイト広告を含んでいます
明けましておめでとうございます。りけーこっとんです。
皆さんは日々積み重ねていること、地道な努力を頑張っていることはありますか?
りけーこっとんは入社前に統計学の基礎だけでも固めておこうかな、と思ってます。
そこで今回は「データ分析のための統計学入門」のまとめの第三弾!
第三章の内容を分かりやすくまとめてみたいと思います。
前回からの続きですね。
第一弾はこちら。
それに引き続き、第二弾はこちら
「データ分析のための統計学入門」 とはアメリカのデータサイエンティストの方々が統計について、統計をどう実際の分析や現場に利用していくかを執筆したもの。
「アメリカの人が書いたって事は、英語…?読める気がしない…」
という方も日本語訳があるので大丈夫!(日本語無料版には、練習問題の解説が付いていません)
これから統計を学ぶ人たち、データサイエンティストを目指す人たちは、読んでおいて損はないと思います。
日本統計協会も「大学で初めて統計学を学ぶ学生、ビジネスでデータ分析をしている社会人のために
書かれた豊富で実践的な練習問題を含む最適な統計学入門書」というお墨付き。
何よりも魅力的なのは、無料公開という点!
統計学についてド素人な自分にとって、どの書籍を買ったら良いか分からなかったので、すごくありがたいです。
下のURLから、無料公開されているページに飛べます。
http://www.kunitomo-lab.sakura.ne.jp/2021-3-3Open(S).pdf
今回の記事は「読む前にさらっと概要を知りたい」という人向け。
より厳密な内容、詳しい内容は原文を読んで貰いたいと思うので、ここでは概略を絵を使ってさらっていきたいと思います。
では早速始めていきましょう。
第三章の概略
第三章は「確率」という題目。
ここでは確率の基本的なところを記述しているようです。
りけーこっとんは高校では理系だったので、高校数学くらいの基本は完全に覚えていなくても「そんなことあったなぁ」くらいには覚えていました。
確率の考え方は統計学の基礎であるらしく、これを理解することは重要っぽそうですね。
りけーこっとんが、この章で学んだことは主に以下の三つ!
・確率とは何か
・条件付き確率とは何か
・確率変数とは何か
自戒の意味も込めて、この基本を押さえておくことは大事です。
統計学は確率を基礎にしているため、統計学を学ぶならば、確率については抑えておきたいところ。
高校でやったきりのりけーこっとんは、忘れている部分も多かったので、一緒に復習も含めて見ていきましょう。
確率とは何か
りけーこっとんが、この章で学んだことの一つ目は「確率とは何か」について。
確率って「正確な定義は?」と聞かれると答えられないですよね。
確率というのは明確に定義すると「実際にどの事象が起こるか分からない(ランダム過程)中で、それぞれの事象が起きる割合」のことです。
難しいですね…
でも、正確に定義するとこうなるようです。
具体例を挙げて説明すると
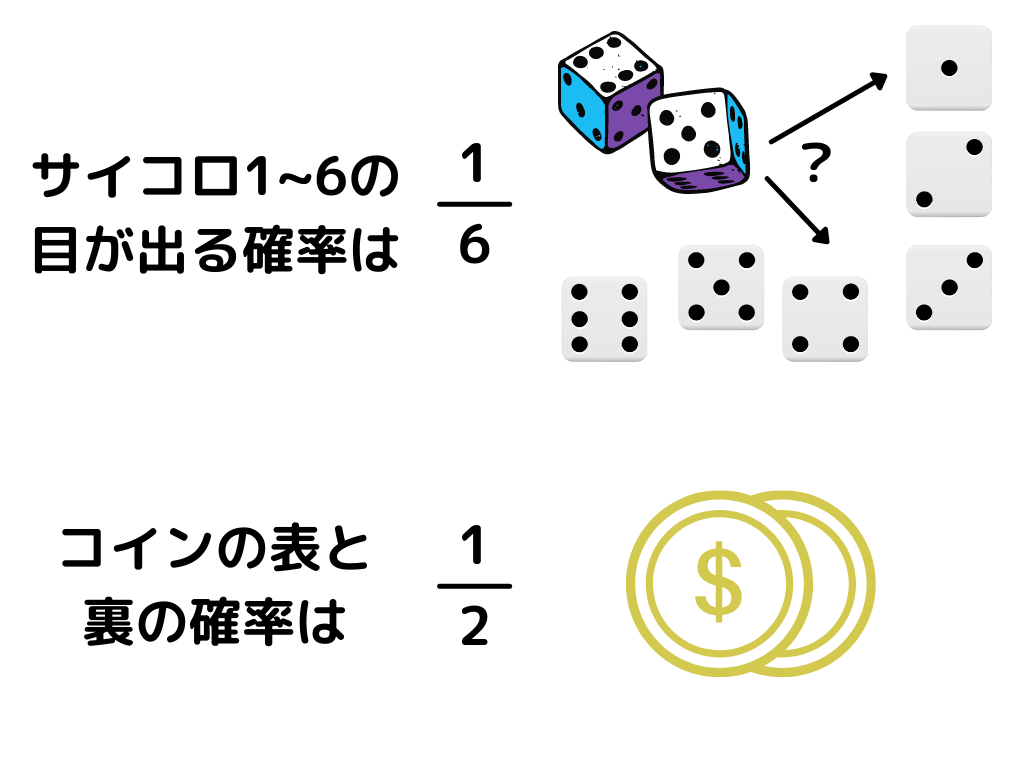
このように言われると、感覚的には分かりやすいのではないでしょうか。
コインの場合、実際に振ってみないと表裏どっちが出るかは分からないけど、表が出るのは50%、裏が出るのも50%ということになります。
これが「実際にどの事象が起こるか分からない(表裏のどっちが出るか分からない)中で、それぞれの事象(表・裏それぞれが出る)が起きる割合(50%)」と言う意味になります。
確率には他にも以下のような特徴があります。
1.試行回数(ex.コインを投げる回数)が多いほど、計算した確率に収束する
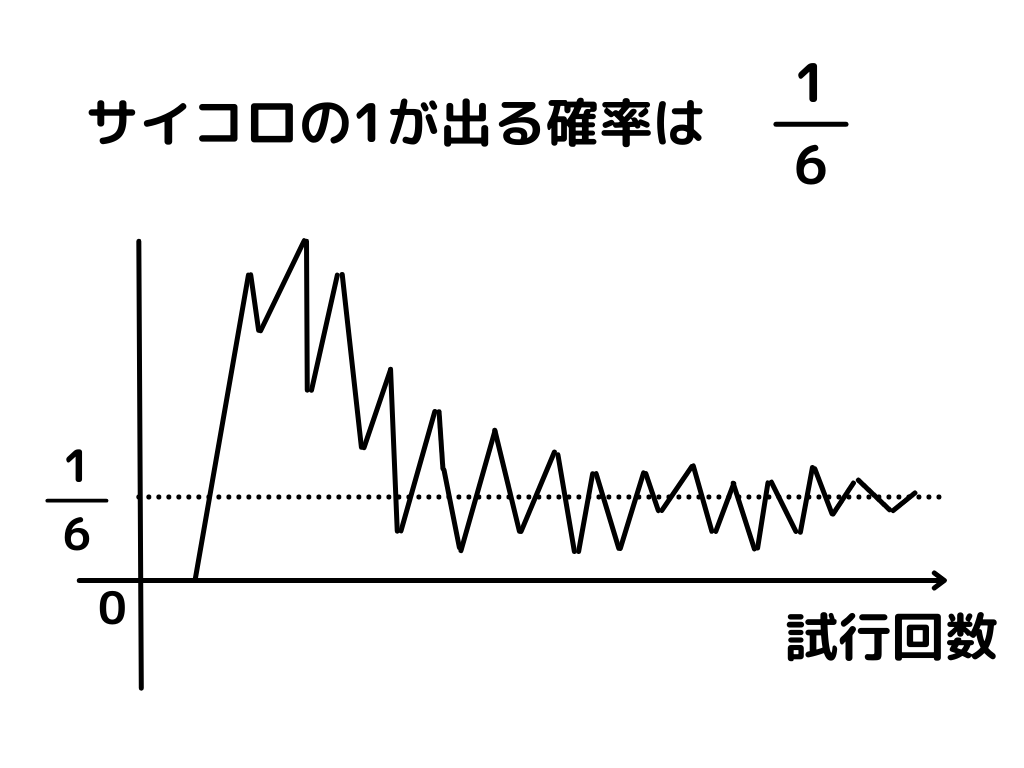
2.確率は、足したり掛けたりできることがある


3.確率は分布を持つことがある
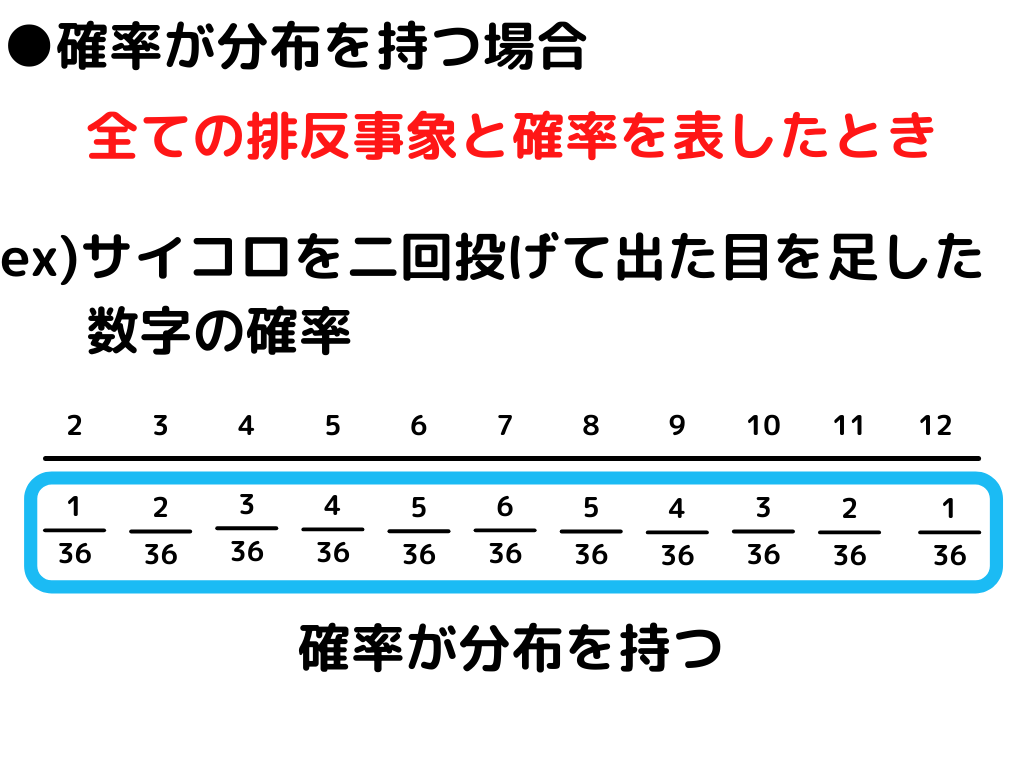
これくらい確率の基礎の基礎から解説してくれているあたり、高校数学を忘れていたりけーこっとんとしては、再確認の意味でもありがたかったですね。
これなら統計学初心者でも、高校数学を習っていない方でも、少しずつ理解を深めていけるのではないでしょうか。

条件付き確率とは何か
りけーこっとんが、この章で学んだ二つ目のことは「条件付き確率とは何か」ということ。
「高校の授業で習った気がするけど…?」
くらいの気持ちでした。
条件付き確率とは、ある条件の下での事象が起こる確率のこと。
例えば以下の画像のようなデータがある場合は、
“女性”という条件下で、その女性が平均以上の身長である確率は●●です。
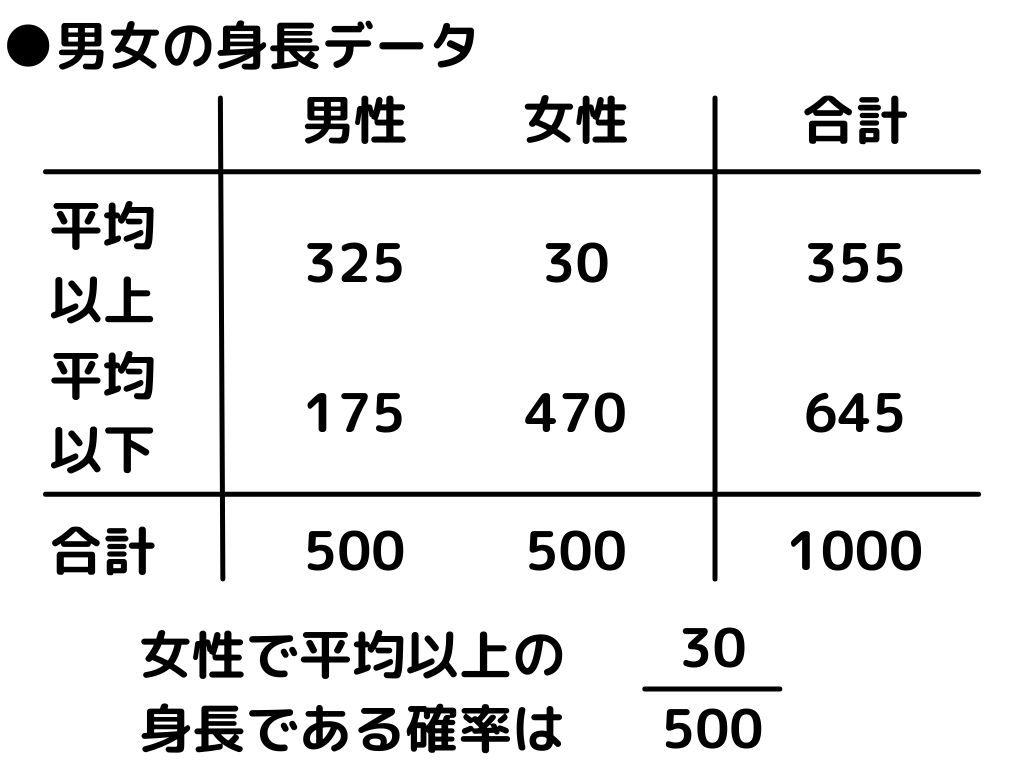
このように条件B(女性)の下で事象A(平均身長以上である)が起こる確率(P(A|B))は次の式で表せます。
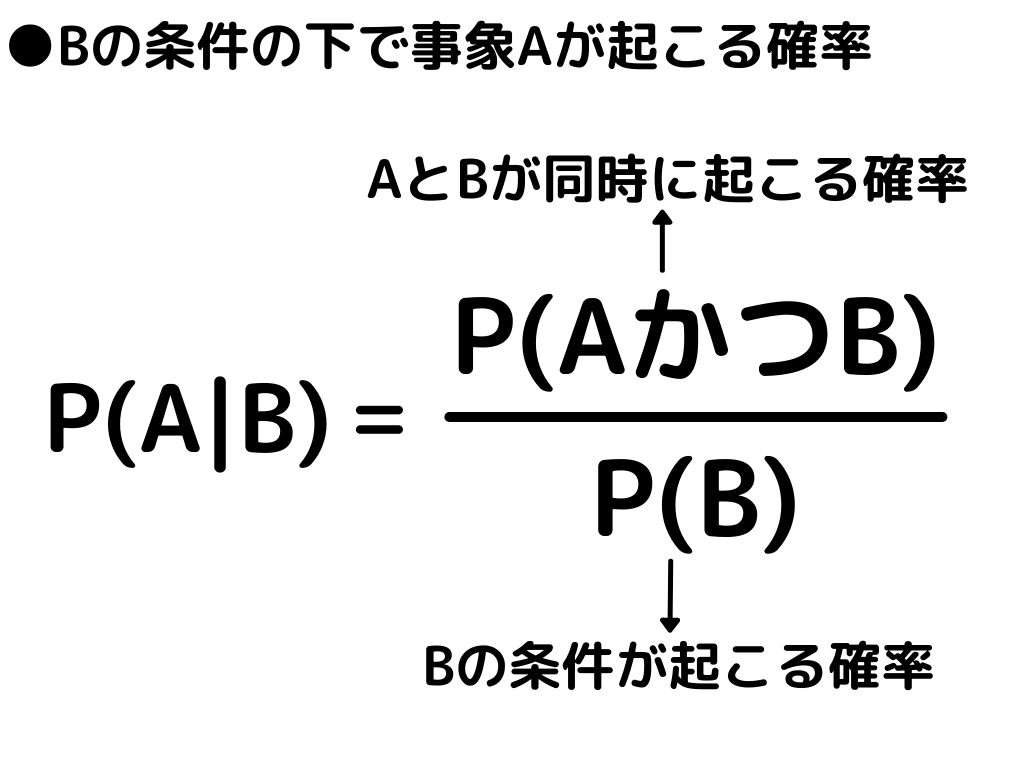
原著では「ボストン天然痘事件」の例を挙げながら、条件付き確率について理解を深める具体的な計算も行っていました。
このように例を用いながら、具体的な計算を解説してくれるのは、より理解が深まりますよね。
また、条件付き確率の発展型として「ベイズの定理」というものがあります。
これはP(A|B)(Bの条件の下でAが起こる確率)が分かっているときに、この反対の条件の確率はどうなるのか、という事を知りたい時に使う定理のこと。
ベイズの定理は「ベイズ統計学」という一つの学問になっているくらい難しいものなので、ここでは公式を書いておくに留めますね。

おそらくデータサイエンティストとして働く上で、ベイズ統計学を学ぶ事は重要だとは思いますが、りけーこっとんが解説するのは早すぎます…
勉強を進めていく中で、理解できたら皆さんに共有したいと思います!
確率変数とは何か
確率変数に関しては、「聞いたことがあるような、無いような…?」という感じでした。
確率変数とは以下のような特徴を持つ変数のこと。
・確率で起こる結果が数値である
・確率で起こる結果が変動する
変数については以下の記事で詳しく触れています。
サイコロの例でたとえると、確率はサイコロの目で1が出る確率は1/6という割合のこと。
この場合、 1~6の間で確率は全部1/6ですよね。
しかし1~6の目は、変化します。
この1~6の出目の数を確率変数といいます。
もう少し複雑な例を見てみましょう。
サイコロを2つ振った時にその合計値が2~12のどれになるかという変動する割合。
この場合、合計値が2~12の間で1/36~1/6まで変動します。
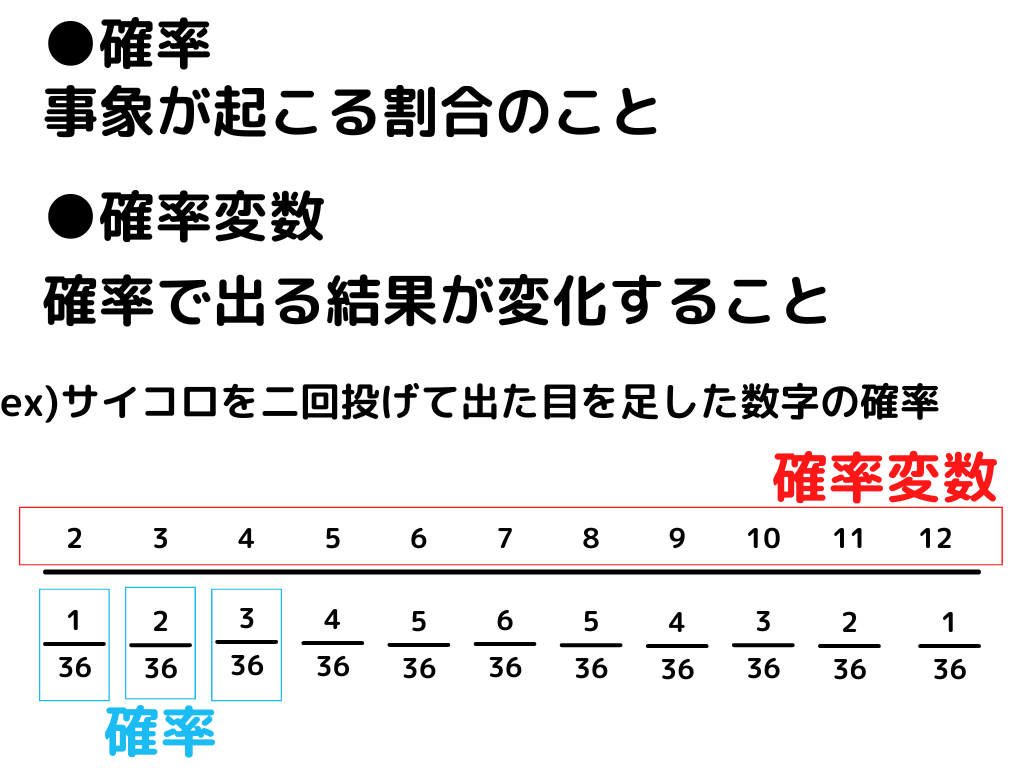
また、結果の事象が数値じゃなくても確率変数とは言えません。
具体的な例は以下の通り。

一つ注意したいのは確率変数でなくても、扱い方によっては確率変数にできるということ。
結果を(裏,表)としてしまえば、確率変数とは言えません。
しかし(裏,表)=(0,1)とすれば数値にできるので、確率変数として扱えます。
他にも確率変数については期待値・分散・標準偏差・線形和など多数扱ってましたが、初心者向けの記事なので、既に書いた基礎の基礎をさらって終わりにしたいと思います。
詳しくは、本書をお読みください。
まとめ
今回の記事をまとめると以下のようになります。

第三章では、統計学の基礎である「確率」を基礎から解説していましたね。
これで初心者の方でも、高校数学を忘れてしまっている人も分かりやすいのかなと思います。
高校時代理系だった、りけーこっとん的には、確率の定義から解説し直してくれている辺りがありがたかったです。
正直、高校数学なんてここ5,6年触れてませんでしたから…
統計学の基礎の、今回は理論的なことを中心にやってきました。
確率自体は、日々の生活で使う場面もあるかと思います。
その際に活かしていただければ幸いですし、りけーこっとんと一緒にデータサイエンスの道へ進む人は、共に頑張りましょう!
ではまた~
続きの第四章は以下のページからどうぞ!









コメント