※本記事はアフィリエイト広告を含んでいます
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/214d380e.96fa3830.214d380f.9c4125c0/?me_id=1213310&item_id=20632239&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F8326%2F9784297128326_1_2.jpg%3F_ex%3D240x240&s=240x240&t=picttext "[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]")
どーも、りけーこっとんです。
DS検定の勉強をしよう！と思ったは良いものの、こんな悩みはありませんか？
DS検定ってどうやって勉強すればいいの？
DS検定の勉強の仕方が分からない…
本で勉強するのは分かるけど、高いなぁ…
無料で単語解説されているサイトとかないかな？
DS検定は、始まったばかりの試験だから、対策法とか分からないよね。
じゃあ、このサイトで出題範囲の内容を押さえていこう～
DS検定の解説をすぐ見たいよ！という方は、以下から最初の解説に飛べます。
今回はスキルチェックリスト
「DS１１３：分析対象を定める段階でバイアスが生じることを理解している」から
「DS１１８：実験計画法の基本的な３原則を説明できる」を解説していくよ～
本サイトでは超重要項目、重要項目、覚えておきたい項目と表記を分けますので、勉強時の参考にしてみてください。
DS検定って、そもそもどんな資格？という方は以下の記事をご覧くださいね。
試験範囲は以下の二つから出題されます。
・スキルチェックリスト
・数理、データサイエンス、AI（リテラシーレベル）モデルカリキュラム
本内容は以下の書籍を参考に作成しております。
なお、本サイトはDS検定の合格を保証するわけではありませんので、ご了承ください。
では早速、内容に入っていきましょう！
※「DS○○：」項目の文章は独自に短縮して表現しております
DS１１３：分析対象を定める段階でバイアスが生じることを理解している
分析を行うに当たって、母集団を全て調べることはできませんよね。
そこで分析する対象を定めるわけですが、決める時点でバイアス（データの偏り）が生じてしまいます。
決める時点で生じてしまうバイアスのことを選択バイアスといいます。
対象を定める時点で注意したいバイアスを以下で見ていきましょう。
脱落バイアス
脱落バイアス
長期的な調査の場合に、途中で対象者が離脱することで生じるバイアス
長期的な調査になると、その途中で脱落者が出てきてしまうことがあります。
例えば地域Aにある世帯の３年間の年収を追跡したい場合を考えましょう。
地域Aにある世帯が３年間変わることなく、常に同じ世帯のみであれば問題はありません。
しかし、転居・転入などにより世帯も世帯数も変わってきます。
このように転居、同意撤回、体調不良など様々な理由で分析対象から外れてしまうバイアスがあります。
自己選択バイアス
自己選択バイアス
分析対象を選ぶ際に、参加者の意志が入り込むことで生じるバイアス
分析対象者を募集する際に生じるバイアスです。
例えば学校の新しい授業で、生徒の成績が向上するかを知りたい場合を考えましょう。
ただし、新しい授業を受けるかどうかは生徒自身が決めます。
この場合そもそも新しい授業を受けようとするのは、真剣に取り組んでいる生徒だけですよね。
真剣な生徒しか集まらないので、新しい授業を受けた生徒の成績は良いことが予想できてしまいます。
このように分析対象者の意志が入り込まないようにすることも大切です。
欠測データバイアス
欠測データバイアス
データの一部に欠損があることによって、データ入手時点で偏りが生じてしまうバイアスのこと。
アンケートなどで集計した際に、答えた人と答えない人の間でバイアスが生じてしまうことですね。
例えば、日本人の年収をインターネットアンケートで調べたいとしましょう。
もし回答してくれる人に学生や無職の人たちが多ければ、年収は低いものになりますね。
この時、サラリーマンなどのデータが欠損しています。
逆に経営者等が多ければ、高く出てしまうかもしれません。
上記以外にも様々なバイアスがあるので、分析対象を定める時点から注意することが大切です。
DS１１７：標本誤差、サンプリングバイアスを説明できる
この項目は「標本誤差」「サンプリングバイアス」を理解しているかどうか、という項目。
この二つの違いとしては、「母集団の特徴を反映できているかどうか」でしょう。
以下で詳しく見ていきます。
標本誤差
標本誤差
母集団を特徴づける値（母数）において、標本から得られる母数と母集団から得られる母数との差のこと。
例えば母集団の平均値が50だとしても、母集団からサンプリングした標本も平均値50になるとは限りません。
標本の平均値が52だとしたら、標本誤差は2になります。
実際には取り出す標本ごとに母数が変わってしまうので、正確に標本誤差を出すことはできません。
そこで言葉は似ていますが、標準誤差という指標を使って確率的に判断できます。
標準誤差が小さいほど、標本ごとの標本誤差のばらつきは小さいという判断が可能です。
標本誤差のばらつきが小さければ、標本での平均や分散が母集団の母数（平均・分散など）に近いと分かります。
サンプリングバイアス
サンプリングバイアス
不適切なサンプリング方法で、母集団特徴を上手く反映できないこと。選択バイアスの一種。
選択バイアスとは、「DS１１３：分析対象を定める段階でバイアスが生じることを理解している」でも触れたものです。
分析する対象を定めた時点で生じてしまうデータの偏りのことでしたね。
その中でも「サンプリング方法」に問題がある場合のことを指します。
例えば、日本の世帯年収を知りたいとしましょう。
ここで東京都内の世帯をランダムサンプリングしたらどうなるでしょうか。
「日本全体」の世帯年収を知りたいのに、東京だけのデータになってしまいますね。
一般的にサンプル数が多ければ多いほど、標準誤差は小さくなります。
しかし東京だけのデータでは、どれだけサンプル数を増やそうが東京のデータしか入らないので、母集団の特徴を反映できないでしょう。
さらに地域の話だけでなく、職種や企業規模、年齢などにも影響されるかもしれません。
そうすると、年齢・地域・職種・企業規模などから均一にサンプリングできる「層化抽出法」などが適しています。
このようにサンプリング方法を間違えてしまうと、母集団の特徴を上手く反映できないので注意しましょう。
DS１１８：実験計画法の基本的な３原則を説明できる
実際の実験では「結果に与えた要因は何か」を調べる時などに、複数の要因に何個かの水準を設けて実験を行います。
例えば、コンビニでアイスの売り上げが伸びたとしましょう。
この時「なぜ売り上げが伸びたか」の要因が分かれば、さらに売り上げを伸ばせるかもしれません。
今回は、要因と考えられるものは「気温」「立地」「配置」とします。
この要因に水準を考えます。（今回はそれぞれ2水準で考えたいと思います）
・気温→「25℃以上」「25℃以下」
・立地→「駅前」「幹線道路沿い」
・配置→「入り口付近」「レジ付近」
すると、要因全ての組み合わせを実験するのに\(\displaystyle 2^3=8\)回実験を行わなければなりません。
もしこれが7水準になったら\(\displaystyle 2^7=128\)回の実験が必要に…
全ての実験を行おうとしたら時間も費用もかかってしまいますね。
そこで、実験回数を削減するのに便利な方法が「実験計画法」です。
実験計画法
実験計画法
効率的にデータを取得して、費用・時間を短縮して解析できる手法のこと。「結果に与えた要因は何か」を検証する際に用いられる統計的手法。
実験計画法はイギリスの統計学者R.A.フィッシャーによって開発された手法です。
基本的には分散分析という手法がとられ、母平均に差があるかどうかを検定します。
しかし、上記でも述べたように「要因」「水準」が増えてくると、全ての組み合わせの実験を行うことは不可能になりますね。
このような場合に「直交表」を用いて実験回数を削減します。
例えば3因子、2水準の場合以下のような直交表が使用可能。
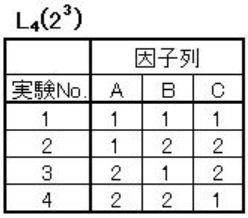
本来は\(\displaystyle 2^3=8\)回の実験が必要なところが4回に抑えられます。
さらに7因子、2水準の場合は以下の直交表になります。
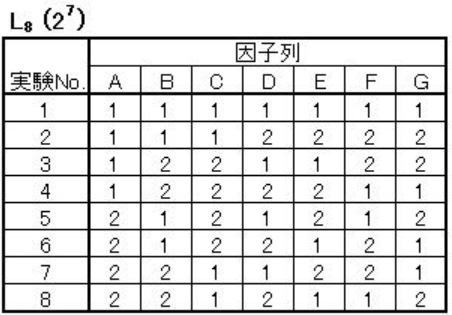
この場合、全ての組み合わせの実験をするには\(\displaystyle 2^7=128\)回の実験が必要に。
しかし8回の実験で確かめられるというのですから、便利な表です。
実験計画法の３原則
実験計画法の３原則
以下の三つがある。（この章の始めで述べた例を用います）
・反復
いくつかの処理や水準に対して実験を繰り返す
例）
アイスの配置を「入り口付近」と「レジ付近」にした場合の売上データをそれぞれ数日ずつ取る
・局所管理
実験の場所や時間などの、結果に影響を与えると思われる条件を局所的に管理する
例）
気温が「25℃以上」のみの店舗でデータを取得する。そして、アイスの配置を「入り口付近」と「レジ付近」にした場合で実験する
・無作為化
実験の場所や時間などの、結果に影響を与えると思われる条件をランダムに入れ替える
例）
複数回の実験の中で、アイスの配置が無作為になるように入れ替える
「反復」を行う理由としては1回の実験だけで差が出たと言っても、たまたま生じた誤差の可能性があるからです。
そのため複数回データを取ることで、「本当の誤差」なのか「偶然出た誤差」なのか分かりますね。
「局所管理」する理由としては、影響を与えると思われる要因（上記の例の場合「立地」など）を排除したいことが挙げられます。
そうすることで比較したい要因の影響だけが分かるようになります。
上記の例で複数回データを取る店舗（反復）を「立地が駅前」に絞ったとしましょう。
すると立地は同じ条件なので「気温」や「アイスの配置」の影響が正確に分かる、といった感じですね。
「無作為化」する理由としては、思わぬ要因の影響を受けないようにするためです。
例えば上記の例でデータを3日間、取りたいとしましょう。
この時、同じ店舗で3日間ともアイスの配置を「入り口付近」にしていたら、データが偏ってしまいますよね。
そのため、この3日間では同じ店舗でも「入り口付近」と「レジ付近」でランダムに変える必要があります。
まとめ
今回は「バイアス・実験計画法」などを解説してきました。
以下の項目を説明できるようになっているでしょうか？
・脱落バイアス
・自己選択バイアス
・欠測データバイアス
・標本誤差
・サンプリングバイアス
・実験計画法
・実験計画法の三原則
DS検定は覚える内容が多いです。
一つ一つを細部まで見るというよりは、広く浅く見ていくことが重要かと思います。
DS検定を取得して、データサイエンティストやAI関連の仕事への道を開きましょう！
次回は「ダミー変数・正規化」などについて解説していきます。
ではまた～
DS検定の続きの解説は以下のページからどうぞ！
コメント