※本記事はアフィリエイト広告を含んでいます

どーも、りけーこっとんです。
「G検定取得してみたい!」「G検定の勉強始めた!」
このような、本格的にデータサイエンティストを目指そうとしている方はいないでしょうか?
また、こんな方はいませんか?
「なるべく費用をかけずにG検定取得したい」「G検定の内容について網羅的にまとまってるサイトが見たい」
今回はG検定の勉強をし始めた方、なるべく費用をかけたくない方にピッタリの内容。
りけーこっとんがG検定を勉強していく中で、新たに学んだ単語、内容をこの記事を通じてシェアしていこうと思います。
結構、文章量・知識量共に多くなっていくことが予想されます。
そこで、超重要項目と重要項目、覚えておきたい項目という形で表記の仕方を変えていきたいと思いますね。
早速G検定の中身について知りたいよ!という方は以下からどうぞ。

具体的にどうやって勉強したらいいの?
G検定ってどんな資格?
そんな方は以下の記事を参考にしてみてください。
なお、りけーこっとんは公式のシラバスを参考に勉強を進めています。
そこで主な勉強法としては
分からない単語出現 ⇒ web検索や参考書を通じて理解 ⇒ 暗記する
この流れです。
試験日は2022年7月2日。(記事の更新は間に合いませんでした)
残り一か月強で、知識0から合格できるかはわかりませんが、頑張りたいと思います。
皆さんも一緒に頑張りましょう!
※この記事は合格を保証するものではありません
大項目「数理・統計」
G検定のシラバスを見てみると、試験内容が「大項目」「中項目」「学習項目」「詳細キーワード」と別れています。
本記事は「大項目」の「ディープラーニングの社会実装に向けて」の内容。
その中でも「数理・統計」というところに焦点を当ててキーワードを解説していきます。
G検定の大項目には以下の8つがあります。
・人工知能とは
・人工知能をめぐる動向
・人工知能分野の問題
・機械学習の具体的な手法
・ディープラーニングの概要
・ディープラーニングの手法
・ディープラーニングの社会実装に向けて
・数理統計
とくに太字にした「機械学習とディープラーニングの手法」が多めに出るようです。
さて、いよいよ最終章の「数理・統計」。
基本的には確率・統計学の分野が出題されます。
やったことない、覚えてないという人でも大丈夫!
基礎的な用語は暗記、計算問題は基本を押さえれば解けます。
シラバスの内容から、統計検定三級の基本的な用語の一部を押さえていきたいと思います。
データの種類
まず「データの種類」について見ていきましょう。
ここで触れるのは「変数」と「尺度」の種類です。
データ(変数)の種類は「量的変数」「質的変数」の二種類。
量的変数:数値として意味があり、+-×÷などの計算ができます
ex)身長、体重、温度、西暦 etc…
質的変数:数値に数としての意味はなく、種類を区別するために用いられる数字です
ex)5段階満足度調査、学校の成績、男性に0女性に1を割り振る etc…
さらに、それぞれの変数は二種類ずつの尺度に分けることができます。
分かりやすく示したのが、以下の図。
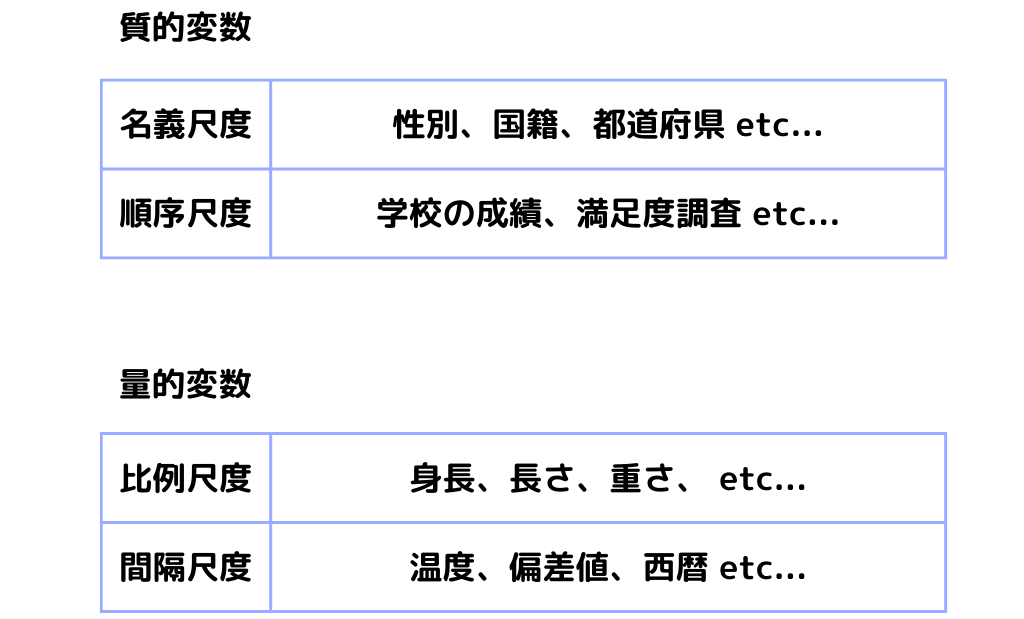
変数と尺度の具体例
名義尺度:物事を区別するためだけに割り当てられた変数です。女性が男性よりも1大きいって意味が分かりませんよね。
順序尺度:大小関係だけ意味を持つ変数です。学校の成績は5が高く、1が低いですよね。しかし5の成績はみんな同じ学力かと言われればそんなことはありません。
比例尺度:一番数字らしい変数でしょう。身長・体重・長さなど+-×÷の計算や平均値を求めることに意味がある変数です。
間隔尺度:絶対的な0を持たず、比に意味がない変数です。摂氏温度が10から20℃になれば10℃上がったとは言えます。しかし2倍の暑さにはなりませんよね。
この中では、間隔尺度が一番イメージしにくいかもしれません。
その変数の0を考えたときに、変数がなくなるかどうかを考えるといいでしょう。
長さなどは0になれば「長さは無い」ということになりますよね。
一方、摂氏温度は0になっても「温度が無い」ということにはなりません。
※絶対温度は0になると「温度が無い」ので、比例尺度です
具体例として温度(摂氏)、西暦、偏差値あたりを覚えておけば問題ないかと思います。
統計学
統計学といっても、一般的に三種類あります。
・記述統計学
・推測統計学
・ベイズ統計学
以下でそれぞれについて見ていきましょう。
記述統計学
手元にあるデータの分析を行うための学問。データの特徴を代表値で表したり、散らばり具合を調べたりします。
キーワード:平均値、最頻値、標準偏差、最大値、散布図、箱ひげ図、相関係数 etc…
推測統計学
手元のデータがどんな分布になっているか推測する学問。確率・確率分布・推定・検定などを扱います。
キーワード:独立、排反、条件付確率、正規分布、二項分布
ベイズ統計学
ベイズの定理を使って、物事が起こる確率を予測する学問。手元にデータが無くても、新しく得たデータを考慮しながら確率を予測します。
キーワード:ベイズの定理、ベイズ推定
それぞれの分野が独立で使われることはあまりなく、目的に応じて使い分けることが重要です

標本調査
では統計学を用いたデータ分析を行いたいとしましょう。
データ分析をするには、まずデータを集めなければいけませんね。
このデータ収集に関するキーワードを本章では見ていきましょう。
母集団
データ分析したい対象全体のこと。
ex)
A高校の平均身長を知りたい ⇒ A高校に通う高校生全員
B県の標準的な朝食を知りたい ⇒ B県に住む人全員
母集団を調べられれば、最も正確なデータ分析を行うことができます。
全数調査
母集団の全データを調べること。具体例は「国勢調査」。
しかし母集団すべてのデータを集めるというのは、時間的にもコスト的にも現実的ではありません。
そこで、標本を抽出します。
標本
母集団から一部を抽出したデータ群のこと。
ex)
A高校の平均身長を知りたい ⇒ 全クラスから5人ずつ調べる
B県の標準的な朝食を知りたい ⇒ 街頭アンケートで100人に答えてもらう
ここで問題になるのが、標本の取り出し方。
抽出方法には以下のようなものがあります。
単純無作為抽出法
くじ引きのように、完全にランダムな方法で標本抽出する
層別標本抽出法
条件の似たグループに分け、それぞれのグループから標本抽出する
集落抽出法
母集団をいくつかのグループに分け、グループをランダムに選ぶ。選んだグループを全数調査。
多段抽出法
母集団をいくつかのグループに分け、グループをランダムに選ぶ。選んだグループからランダム抽出。
以下の記事では図を使って分かりやすくまとめていますので、ぜひご覧ください。
統計グラフ・表
集めたデータは、グラフや表にして可視化することで見やすくなります。
G検定で重要なグラフは、ヒストグラム・散布図・箱ひげ図、あたりでしょうか。
表には度数分布表・クロス集計表があります。
まずはどんなグラフかのイメージをつかみましょう
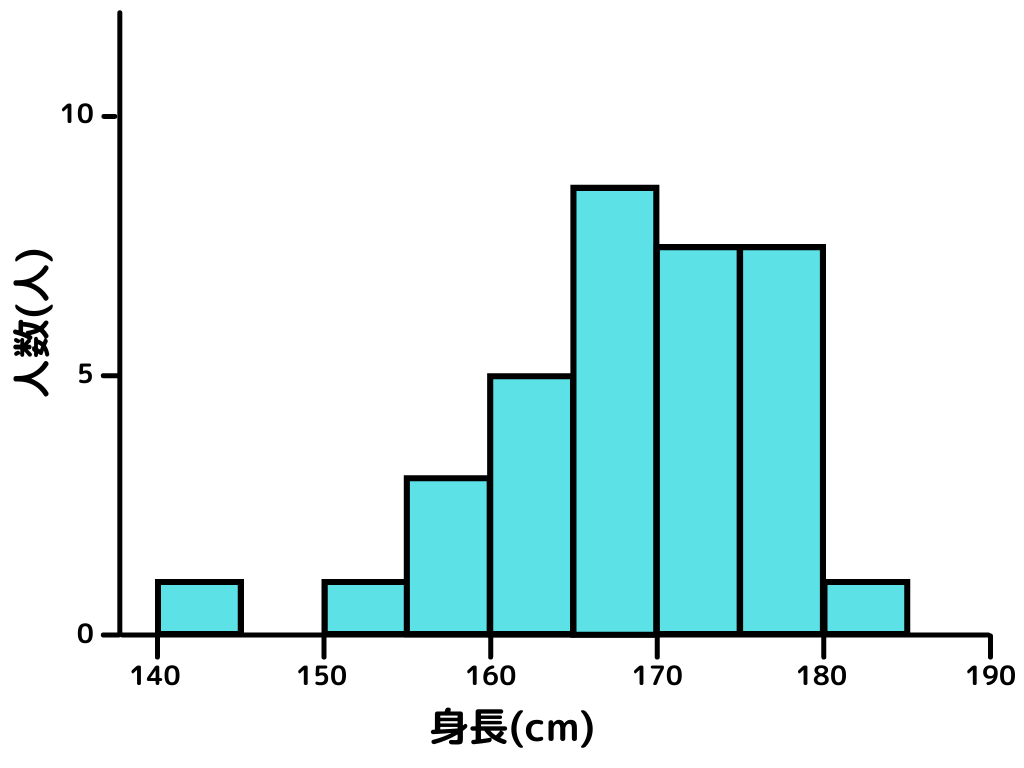
ヒストグラム
データを一定の範囲に区切って、その間にあるデータ数を数えたグラフ。
詳しくは「データの集計」の章で解説します。
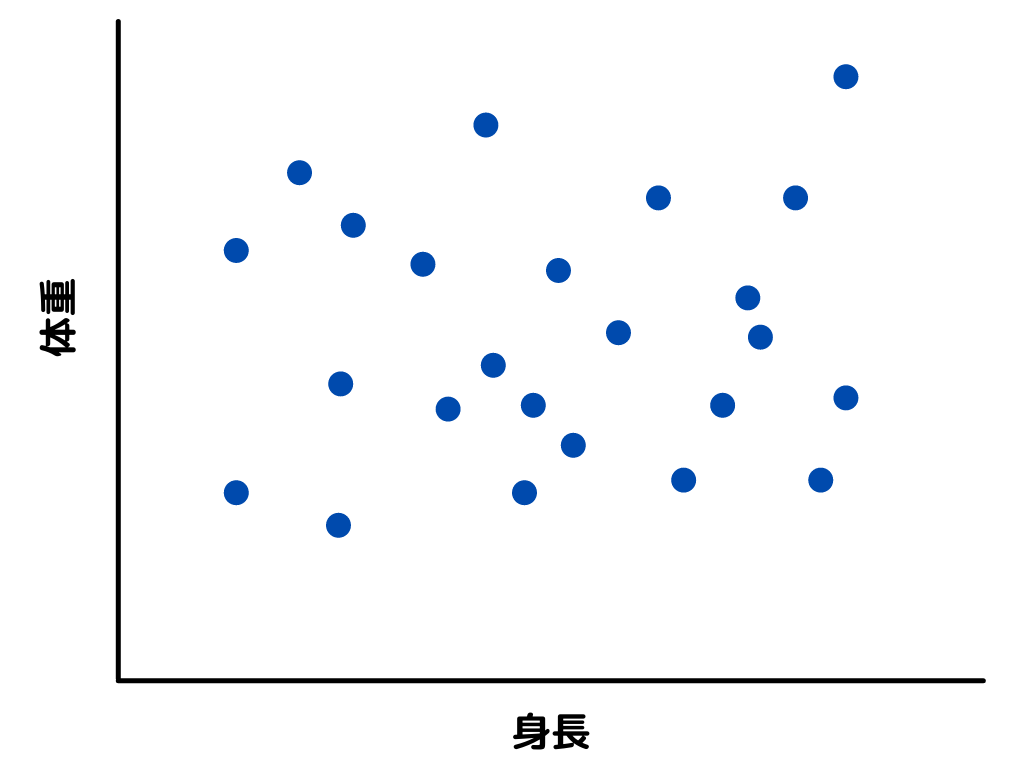
散布図
データを一つ一つの点で打っていったグラフのこと。
詳しくは「データの散らばり」の章で解説します。
箱ひげ図
箱とひげを使って、データ全体の特徴を表すグラフのこと。
詳しくは「データの散らばり」の章で解説します。
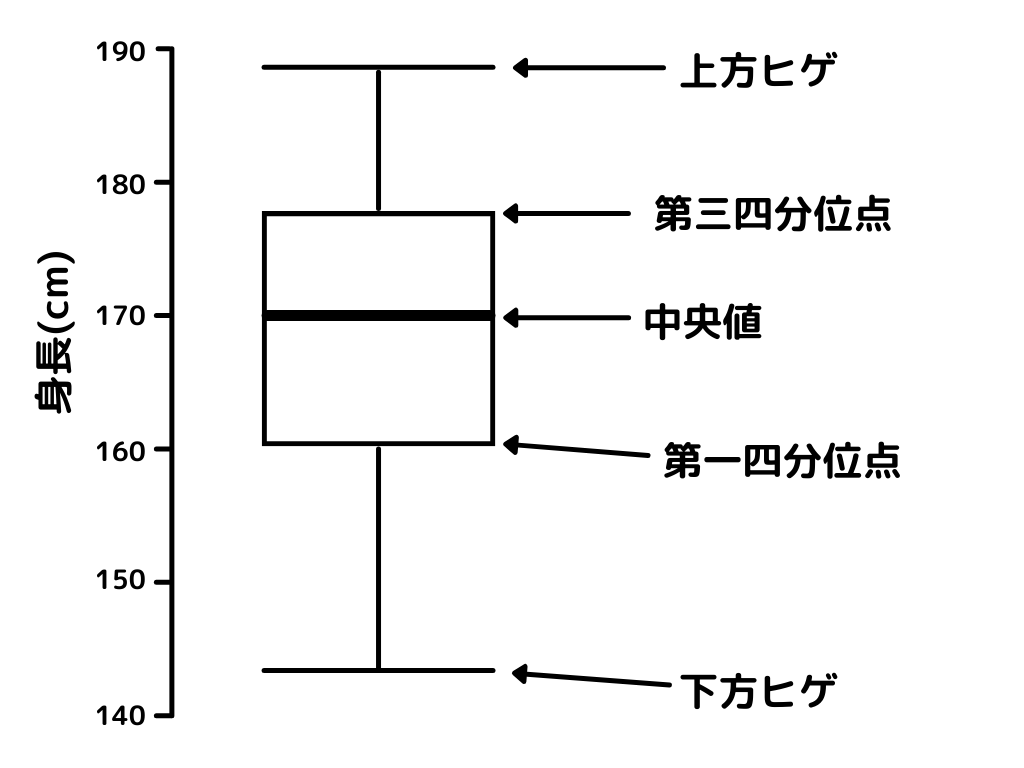
上方ヒゲが「最大値」、下方ヒゲが「最小値」。
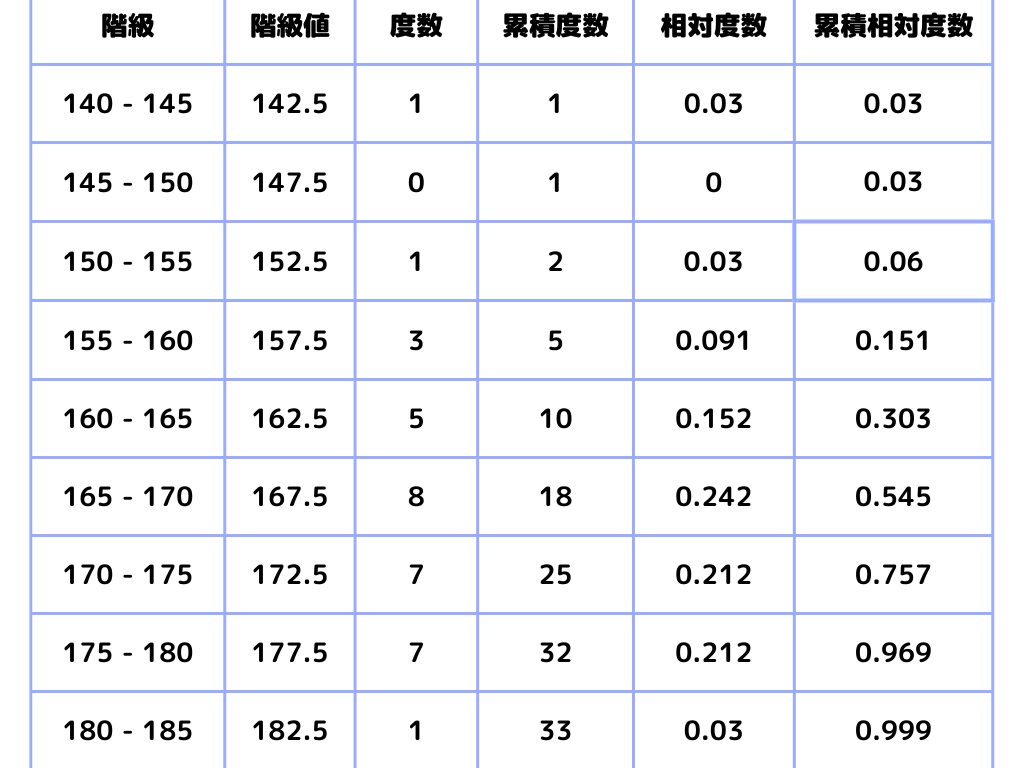
度数分布表
データを一定の範囲に区切って、その間にあるデータ数を数えた表。この表をグラフにすると、ヒストグラムになります。
詳しくは「データの集計」の章で解説します。
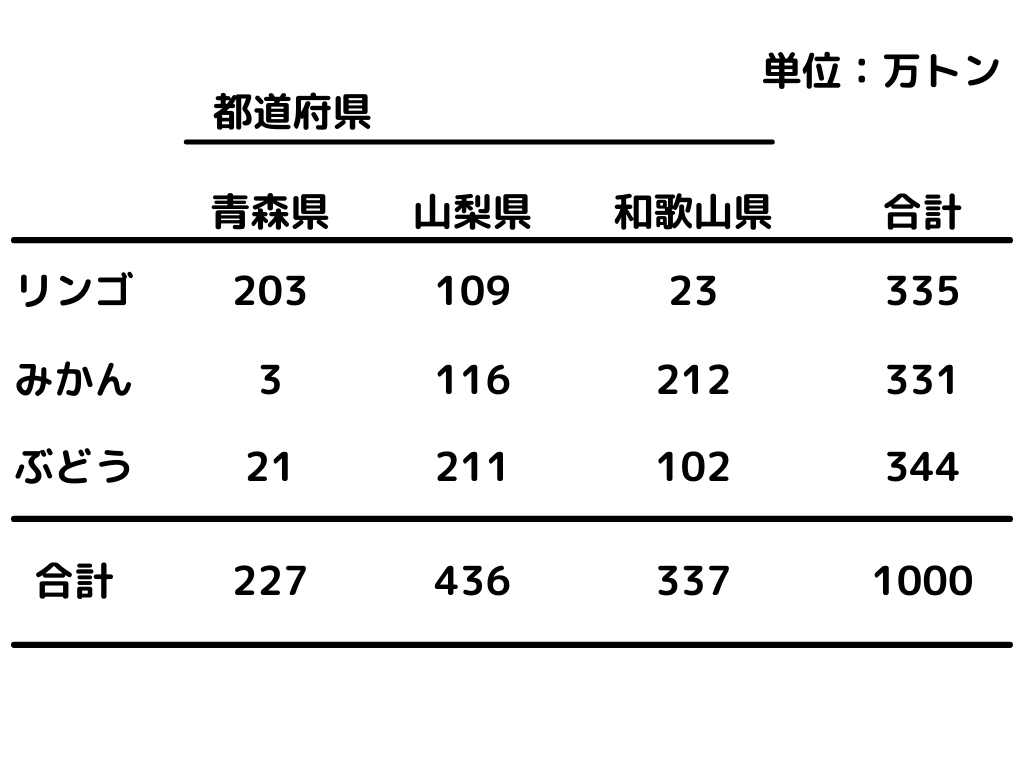
クロス集計表
表の縦と横に「質的変数」を入れて、縦と横がクロスする部分に該当する値を記入する表。

データの集計
先ほど出てきたヒストグラム、度数分布表について詳しく見ていきましょう。
「標本調査」で集められたデータも、そのままの状態では使いにくいし、何も見えてきません。
そこで「集計」を行って、どんなデータがあるのか分かりやすくします。
分かりやすいのが、表にするという方法ですね。
そこで「度数分布表」や「クロス集計表」を作成すると役に立ちます。
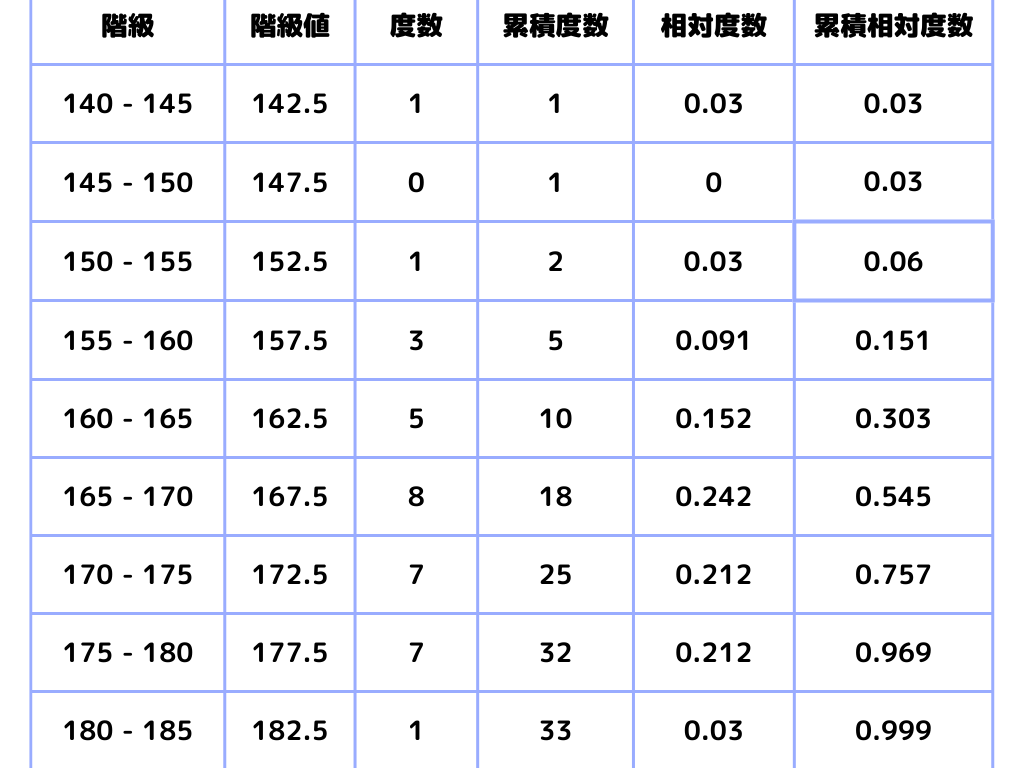

こうすると「165~170 cmが一番多いんだな」とか「青森県はリンゴを203万トン生産したのか」ということが分かりますね。
ここで「度数分布表」の用語について解説します。
階級
1変数(今回は身長)を一定間隔で区切った際の、間隔のこと。
階級値
階級を代表する値。階級の真ん中の値が階級値。
度数
今回のグラフでは「人数」。階級の間にあるデータの個数のこと。
累積度数
その階級までの度数の和。
相対度数
それぞれの階級の度数が全体に占める割合のこと。
※表のデータは四捨五入の関係で全て足しても1から若干ズレます
\(\displaystyle \frac{各階級の度数}{全度数}\)
累積相対度数
その階級までの相対度数の和。
※本当は最終的に1になりますが、四捨五入の関係でズレがあります
そして「度数分布表」からは「ヒストグラム」を作成できます。

縦軸は分かりやすく「人数」と書いていますが、要は「度数」のこと。
「身長」という1変数を横軸にとって、縦軸は「度数」を表したグラフがヒストグラムです。
データの散らばり
次に「箱ひげ図」「散布図」を見ていきましょう。
「身長」データの箱ひげ図は、以下のように表記します。

この図の見方を解説していきます。
最小値・最大値
データの一番小さい値と大きい値。最小値が下方ヒゲ、最大値が上方ヒゲにあたる。
範囲
データ全体の範囲のこと。\(最大値 – 最小値\)
中央値
データを小さい順に並べたときに、データ数で真ん中にある値。
四分位数
データを小さい順に並べたときに、四等分にした時の区切り点。
ex) 1, 2, 4, 7, 9, 19, 30の場合
第一四分位点:2、第二四分位点(中央値):7、第三四分位点:19
四分位範囲
四分位数の範囲のこと。\(第三四分位点 – 第一四分位点\)
次に「身長」に加えて「体重」も測ったとしましょう。
すると以下のデータが得られたとします。
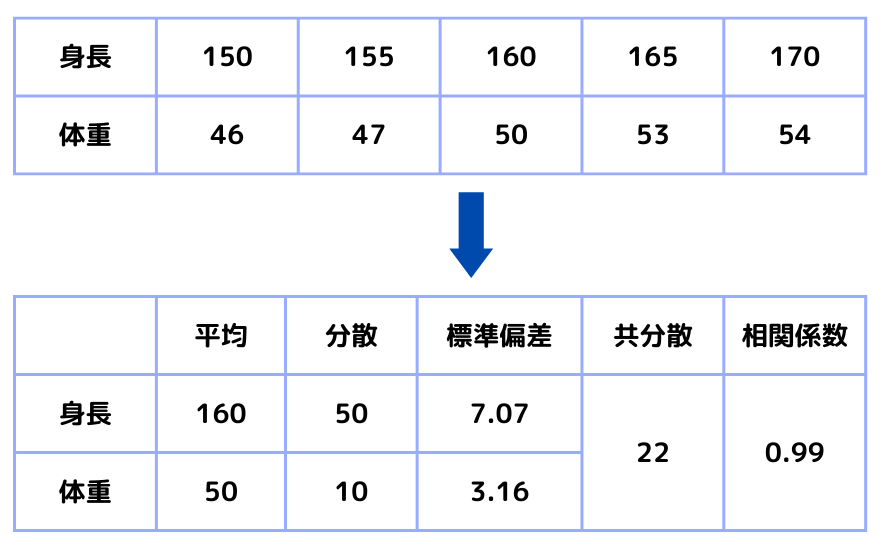
この時、以下の指標を計算することでデータの散らばりが分かります。
分散\(\sigma^2\)
平均(\(\bar{x}\))との差の二乗を全データで足したもの。\(x_k\)はそれぞれのデータ。
\(\displaystyle \sigma^2 = \frac{1}{n}\times\sum_{k=1}^{n}(x_k – \bar{x})^2\)
標準偏差\(\sigma\)
分散にルートを取ったもの。単位が元データと同じになるので、扱いやすい。
共分散\(\sigma_{xy}\)
2データの平均(\(\bar{x}, \bar{y}\))からの差同士を掛けて、全て足したもの。\(x_k\)、\(y_k\)はそれぞれの変数のデータ。
\(\displaystyle \sigma_{xy} = \frac{1}{n}\times\sum_{k=1}^{n}(x_k – \bar{x})(y_k – \bar{y})\)
相関係数\(r\)
2データに直線の関係があるかどうか(相関)分かる値。
\(\displaystyle r = \frac{\sigma_{xy}}{\sigma_x \times \sigma_y}\)
ちなみに学力でよく使う「偏差値」は以下のような式で表されます。
偏差値
\(\displaystyle 偏差値 = \frac{x – \bar{x}}{\sigma} \times 10 + 50\)
さらにデータを取っていって、以下の散布図が得られたとしましょう。
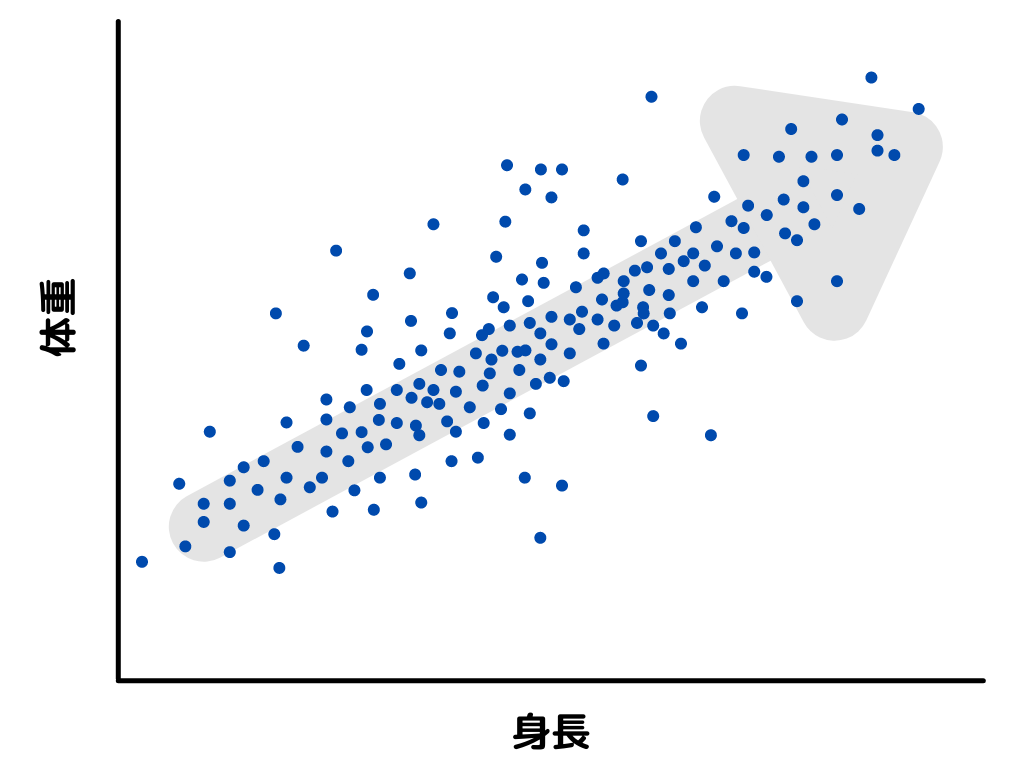
散布図は2変数間にどれだけ相関があるかや、データの散らばり具合が分かります。
データは均一に散らばっていそうですね。
また、身長が伸びれば体重が増えていきそうです。
このように右上に伸びる直線にデータが分布しているので、「正の相関がある」と言います。
相関を定量的に表したものが「相関係数」ですね。
確率分布
この章は「推測統計」のお話です。
確率変数
確率で、起こる結果が変わる数値のこと。
ex) さいころの出目
確率変数については以下の記事で詳しく触れています。
気になった方は、ぜひご覧ください。
確率分布
確率変数と確率の関係を表した分布のこと。横軸に変数、縦軸に確率を取ります。
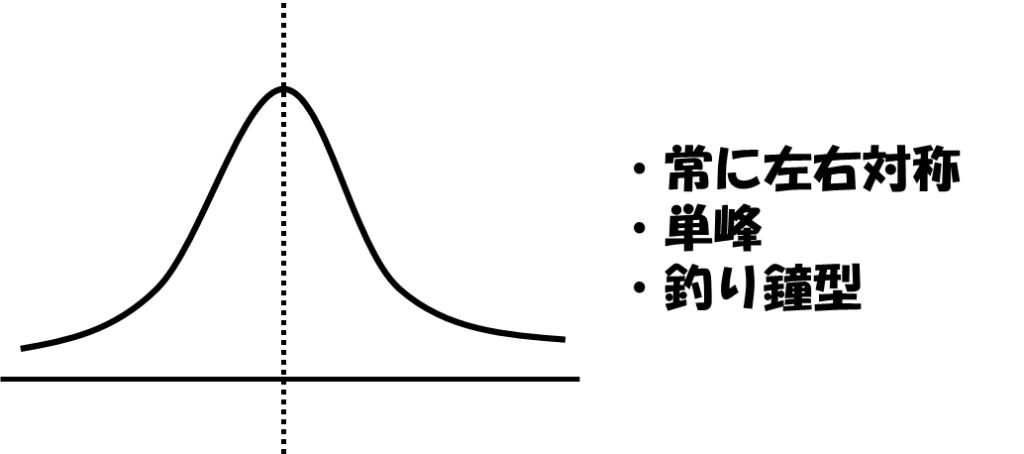
正規分布
最も一般的な確率分布。平均と分散(標準偏差)で、以下の山の形が決まる。
平均が点線部分、分散は山の横の広がりを表す。
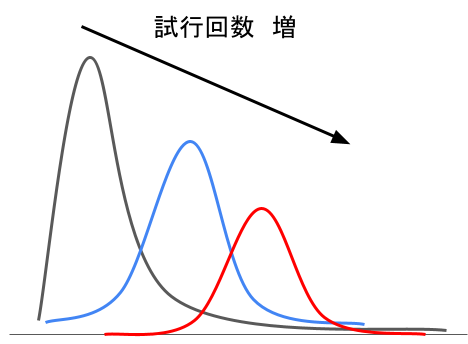
二項分布
正規分布の次に一般的な確率分布。試行回数を増やしていくと正規分布に近づく。
確率分布・正規分布・二項分布については、以下の記事で詳しく解説しています。
興味があれば、見てみてください。
ベイズ統計学
この章は「ベイズ統計」のお話です。
といっても、ベイズ統計で抑えるべきポイントは以下の二つかなと。
ベイズの定理
以下の定義式で表される。ベイズ統計学の最も基本部分。
\(\displaystyle P(A|B) = \frac{P(B|A)P(A)}{P(B)}\)
P(A|B):事後確率(Bであることが分かった場合にAになる確率)
P(B):事前確率(Bが起こる確率)
P(B|A):尤度(Aであることが分かった場合にBになる確率)
P(A):正規化定数(Aが起こる確率)
ベイズ推定
ベイズの定理に基づき、ある事象を推定すること。
新しく得られた情報を、推定に加えて更新する。
ベイズの定理の式だけではわからないと思うので、例題を一つ解きましょう。
あなたはお菓子をX・Y・Z社から仕入れて販売しています。それぞれの会社からの仕入れ量の割合は20・30・50%です。また、それぞれの会社は不良品を6・5・4%の確率で出してしまいます。
ある日、あなたは不良品を見つけました。この不良品がY社の不良品である確率は何%でしょうか。
求めたいのは「不良品がY社のお菓子である確率」なので、これをP(A|B)とします。
P(A|B)の理解の仕方としては、
「B:不良品が発生する」ということが分かった場合、「A:Y社のお菓子である」確率ですね。
なのでP(B)、P(B|A)、P(A)はそれぞれ
P(B):不良品が発生する確率(全社に渡って)
P(B|A):Y社のお菓子であった場合に、不良品になる確率
P(A):Y社のお菓子である確率
となります。
それぞれの確率を求めていきましょう。
P(A)はY社のお菓子である確率なので、30%(0.3)ですね。
P(B|A)は、Y社のお菓子の時に不良品になる確率なので、掛け算になります。
\(\displaystyle P(B|A) = 0.3 \times 0.05 = 0.015\)
P(B)は不良品の発生する確率ですね。これはX・Y・Z社全ての不良品確率を足さなければいけません。
Y社の不良品確率を求めた方法で、X・Z社も求めます。
以上3つの確率を求めたことで、ベイズの定理が使えます。
\(\displaystyle P(B|A) = \frac{0.015\times0.3}{0.047} = 0.0957… \neq 0.096\)まとめ
今回は大項目「数理・統計」についての解説でした。
本記事をまとめると以下の通り。
・量的変数、質的変数
・名義尺度、順序尺度、比例尺度、間隔尺度
・記述統計学、推測統計学、ベイズ統計学
・母集団、標本
・全数調査
・単純無作為抽出法、層別抽出法、集落抽出法、多段抽出法
・ヒストグラム、散布図、箱ひげ図、クロス集計表
・階級、度数、相対度数
・範囲、四分位数、四分位範囲
・分散、標準偏差、共分散、相関係数
・確率変数、確率分布、正規分布、二項分布
・ベイズの定理、ベイズ推定
これらの単語、説明できるようになりましたか?(多すぎましたかね…)
G検定では「機械学習」「ディープラーニング」で覚える内容が多いので、どうしてもそちらに注力します。
正直、「数理・統計」は基本的な内容も多数。
理系大学の方であれば、G検定の「数理・統計」程度であればやったことある人も多いのではないでしょうか。
もちろんやっていなかった方にも、知っている内容はあったと思います。
出題数が多いわけではないので、最低限の重要キーワードだけでも覚えておくことが重要でしょう。
さて、今回でG検定の勉強シリーズは終了!
お疲れさまでした!
一人でも「この記事を見てG検定合格した!」という方がいれば、超うれしいです。
ご報告いただけたら、泣いて喜びます。
次も資格勉強関係の記事を更新していきたいと思いますね。
次は何の資格にしようかな?
ではまた~












コメント