※本記事はアフィリエイト広告を含んでいます

どーも、りけーこっとんです。
「G検定取得してみたい!」「G検定の勉強始めた!」
このような、本格的にデータサイエンティストを目指そうとしている方はいないでしょうか?
また、こんな方はいませんか?
「なるべく費用をかけずにG検定取得したい」「G検定の内容について網羅的にまとまってるサイトが見たい」
今回はG検定の勉強をし始めた方、なるべく費用をかけたくない方にピッタリの内容。
りけーこっとんがG検定を勉強していく中で、新たに学んだ単語、内容をこの記事を通じてシェアしていこうと思います。
結構、文章量・知識量共に多くなっていくことが予想されます。
そこで、超重要項目と重要項目、覚えておきたい項目という形で表記の仕方を変えていきたいと思いますね。
早速G検定の中身について知りたいよ!という方は以下からどうぞ。

具体的にどうやって勉強したらいいの?
G検定ってどんな資格?
そんな方は以下の記事を参考にしてみてください。
なお、りけーこっとんは公式のシラバスを参考に勉強を進めています。
そこで主な勉強法としては
分からない単語出現 ⇒ web検索や参考書を通じて理解 ⇒ 暗記する
この流れです。
※この記事は合格を保証するものではありません
大項目「ディープラーニングの概要」
G検定のシラバスを見てみると、試験内容が「大項目」「中項目」「学習項目」「詳細キーワード」と別れています。
本記事は「大項目」の「ディープラーニングの概要」の内容。
その中でも「学習の最適化」というところに焦点を当ててキーワードを解説していきます。
G検定の大項目には以下の8つがあります。
・人工知能とは
・人工知能をめぐる動向
・人工知能分野の問題
・機械学習の具体的な手法
・ディープラーニングの概要
・ディープラーニングの手法
・ディープラーニングの社会実装に向けて
・数理統計
とくに太字にした「機械学習とディープラーニングの手法」が多めに出るようです。
今回はディープラーニングの概要ということもあって、ディープラーニングの基礎的な内容。
ここを理解していないと、ディープラーニングがどういうものかを理解できません。
ここから先の学習の理解を深めるために、そしてG検定合格するために、しっかり押さえておきましょう。
学習の最適化に関する用語をまとめていきたいと思います。
主にディープラーニングのパラメータの更新の仕方について述べています。
勾配降下法
勾配降下法とは、ディープラーニングの隠れ層のパラメータを更新する手法。
パラメータを更新する目的は何だったか覚えてるでしょうか。
ディープラーニングの基本は「教師あり学習」だったので、予測値と教師データの誤差(関数)を最小にすることが目的でしたね。
つまり、誤差関数を最小値にできるパラメータを求めたいのです。
なんで勾配降下法が使われるかというと、勾配が0になる部分が最小値という事実があるからです。
勾配は関数の傾きで、習った方ならば分かると思いますが、微分を行います。
(具体的なやり方は最急降下法での章で示します)
微分はG検定合格にむけて、以下の式を覚えておけば問題ないかと。

下の式に付いた「’」は「f(x)という式を微分するよ」という意味です。
つまり、微分をするとxの累乗の数をそのまま掛け算して、xの累乗は1減らすという式になっていますね。
微分を行うことで勾配が求められて、最小値が分かるといった流れになっています。
今回は似たようなアルファベットの手法がたくさん出てきます。
しかし、そのすべての基本は勾配降下法です。
最急降下法(GD)
最急降下法(GD)とは勾配降下法の一つで、最も基本的な方法。
全てのデータを使って、勾配降下法を行います。
具体的な手順は以下の通り。
1.モデルの「パラメータ(重み)」を誤差関数に入力
2.「パラメータ」に対する誤差関数の勾配を計算

3.勾配が「+」なら重みが小さくなるように、勾配が「-」なら重みが大きくなるように変化させる
(今のパラメータ) = (前のパラメータ) – (学習率) × (勾配)
※学習率に関しては後の章で触れます

4.2と3を繰り返すことで重みを少しずつ変化させ、勾配がなるべく小さくなる重みを見つける

図のイメージだと、関数の線上にボールを置いたことを考えると分かりやすいですね。
ボールは坂を転がって最終的には坂がないところ、つまり勾配がないところに行きつくというのは想像できるのではないでしょうか。

確率的勾配降下法(SGD)
確率的勾配降下法(SGD)とは、最急降下法よりも効率的に計算を行おうとした勾配降下法のこと。
最急降下法はすべてのデータを使用するので、データが大量になってくると時間がかかってしまいます。(特に最近は)
この問題を解消するために開発されたのが、確率的勾配降下法。
一部のランダムにサンプリングしたデータで、勾配降下法を適用する方法です。
データ量が最急降下法に比べ少なくなるので、より効率的に計算が行え、ビッグデータにも対応しやすいようです。
モーメンタム
モーメンタムとは、確率的勾配降下法(SGD)に慣性的な性質を持たせた手法のこと。
確率的勾配降下法では、最適なパラメータに辿り着く前に、曲がりくねりながら到達します。
SGDに比べ、主な特徴は以下の二つ。
・最小値に付くまでの経路に、無駄がなくなる
・停滞しやすい領域においても、学習が上手くいきやすくなる
最急降下法のところで、ボールが坂を下っていくようなイメージを話しましたよね。
このイメージの通りに、局面に摩擦があることを考えたイメージで式があるのが、モーメンタムです。
以下より、その手法が登場した年代順に書いていきますね。
AdaGrad(2011)
AdaGradとはパラメータ最適化手法の一つで、確率的勾配降下法の改良手法。
モーメンタムとAdaGradでは、どちらも「効率的に最小値に達する」ことを目的としていました。
2つの違いとしては効率化の仕方。
モーメンタムは、曲面に摩擦があることを考慮した式が追加される形で、効率化していましたね。
そして学習率は一定かつ、ハイパーパラメータだったので、分析者の腕による部分もありました。
しかしAdaGradではパラメータ毎の学習率を、勾配を用いて自動的に更新します。
学習が進むほど学習率を小さくすることで「いつまでも学習が終わらない」という事態を避けることができます。
RMSprop(2012)
RMSpropとはパラメータ最適化手法の一つで、AdaGradの改良版。
学習率を調整して「いつまでも学習が終わらない」事態を避けます。
AdaGradと似てはいるのですが、「直近の勾配ほど強く影響する」ようにしたのが、RMSpropですね。
AdaDelta(2012)
AdaDeltaとは、AdaGrad・モーメンタムと別の確率的勾配降下法の改良手法。
最急降下法の章でも出てきた以下の式、覚えているでしょうか?
(前のパラメータ) = (今のパラメータ) – (学習率) × (勾配)
これはパラメータの更新式でした。
実は、この式では単位が揃っていないんです。
「勾配」は、元の関数を微分したものと説明しました。
微分すると、単位が変化してしまいます。
(例えば”m(長さ)”を微分すると”m/s(速さ)”に変わってしまいますが、G検定合格には「そんなもんなのね」くらいがちょうど良いと思います)
「パラメータ」というのは、元の関数に値を代入したものなので、単位は元の関数と同じ。
「学習率」等の”●●率”は単位がありません。
すると上式は、例えば「長さ」ー「速度」という謎の形になっていることが分かりますよね。
そこで、単位を揃えるように調整した手法がAdaDeltaです。
学習率を持たない事が特徴ですね。
Adam(2014)
Adamも確率的勾配降下法を基本とした、ディープラーニングのパラメータ最適化手法の1つ。
モーメンタムとRMSpropの説明を見て、目的が同じということは分かりましたね。
「目的が同じなら、2つを組み合わせれば性能良くなるじゃん」で考えられたのがAdamです。
なので特徴としては、以下の2つ。
・モーメンタムとRMSpropを組み合わせている
・最初は学習率が大きく、段々と小さくしていく
詳しく説明し出すと難しくなってしまいますので、強調した部分を覚えれば良いと思います。
AdaBound(2019)
AdaBoundは、AdamとSGDのいいとこ取りをした手法のこと。
Adamの特徴としては最初は学習率が大きくて、だんだん小さくしていくというものでしたね。
AdaBoundは、序盤はAdamの早い収束性を、終盤はSGDの高い汎用性を再現したものになります。
最初はAdamを使って早く収束させるようにして、終盤はSGDを使って高い汎用性を再現するようにしています。
AMSBound(2019)
AMSBoundとは、AMSGradとSGDのいいとこ取りをした手法のこと。
AMSGradとは、重要な情報がAdamですぐ消えてしまわないようにAdamを改良したもの。
あまりAMSGradとAdamで、明確な性能の差が出たわけではないらしいです。
最初はAdamを使って早く収束させるようにして、終盤はSGDを使って高い汎用性を再現するようにしています。
AdaBoundとAMSBoundは似ているので、注意が必要です。
学習率
学習率とは、一回の機械学習の最適化において、どのくらい値を動かすかのパラメータのこと。
一番最初の「最急降下法」の式で出てきたものです。
式をもう一度見てみると
(今のパラメータ) = (前のパラメータ) – (学習率) × (勾配)
勾配を何倍するかを決めるのが、学習率ですね。
つまり「(学習率) × (勾配)で前のパラメータからどれくらい移動させて、今のパラメータとするか」という式の意味になります。
上式は、一回のパラメータ更新に関する式です。
なので学習率の値が大きいと、一回の更新で次のパラメータは移動が大きくなるということ。
学習率が小さければ、一回の更新でパラメータはそんなに移動しません。
つまり、最適なパラメータを見つけるまでに時間がかかりすぎてしまいます。
では、大きければ大きいほど良いのでしょうか?
答えは「大きすぎるとパラメータが発散し、いつまでも学習が終わらない」です。
なので大きすぎず小さすぎず、最適な学習率を定めるために、今まで紹介してきた様々な方法があったわけですね。
誤差関数
誤差関数とは、損失関数と同義です。
損失関数が何だったか覚えていますか?
以下の図を見れば思い出す人も多いかと。
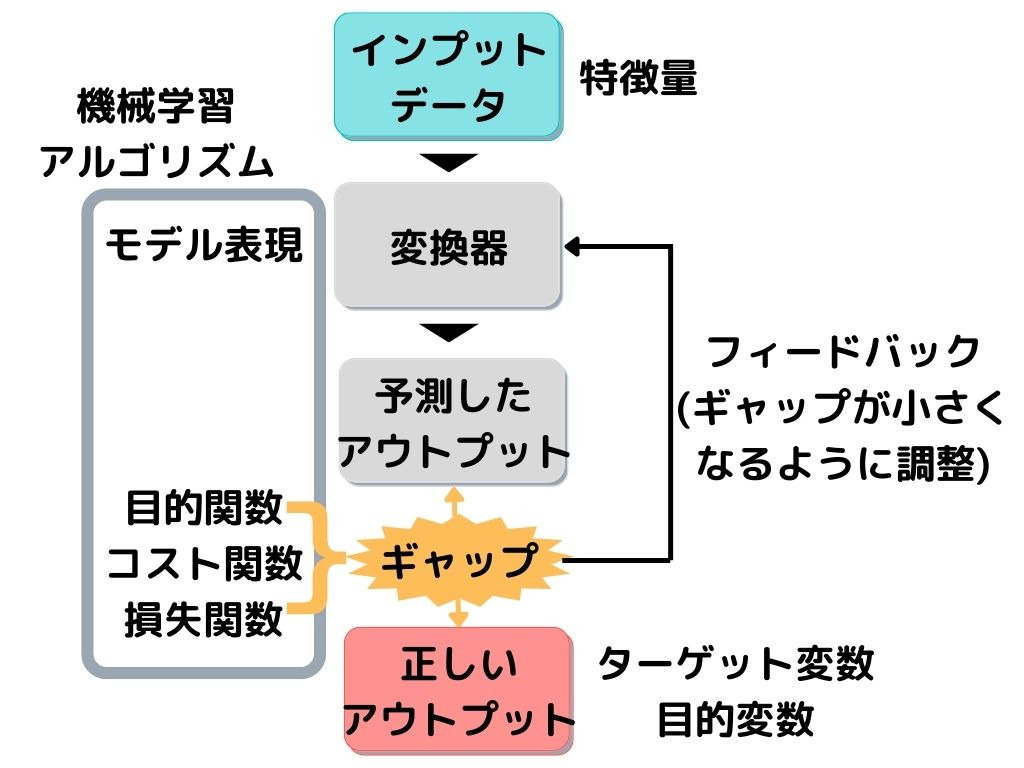
この図は、教師あり学習の一連の流れを示したものでした。
教師データ(目的変数)と予測値の差(ギャップ)が損失関数でしたね。
こう考えると、ギャップの言い方には色々な言い方があるようです。
交差エントロピー誤差関数
交差エントロピー誤差関数とは、誤差関数の一種。
具体的な式は難しいので割愛します。
重要なのは、分類問題の回帰分析で用いられる誤差関数であるということ。
分類問題?回帰問題?と思った方は以下の記事をご覧ください。
イテレーション
イテレーションとは、ニューラルネットワークのパラメータの更新回数のこと。
ディープラーニングでは最急降下法で見たように、何回もパラメータ更新を繰り返します。
この回数をイテレーションというわけですね。
エポック
エポックとは、トレーニングデータ(訓練データ)を何回繰り返し学習させるかの回数。
パラメータ数が多いので、一回トレーニングデータを学習させたところで、精度はあまり良くないんですね。
これはイテレーション数だけを増やしても、です。
なので「イテレーション数で最適化」→「エポック数を増やして、学習」を繰り返すということをやるようです。
まとめ
今回は大項目「ディープラーニングの概要」の中の一つ「学習の最適化」についての解説でした。
本記事の重要キーワードは以下の通り。
・最急降下法
・確率的勾配降下法
・モーメンタム
・AdaGrad
・RMSprop
・AdaDelta
・Adam
・AdaBound
・AMSBound
・学習率
・交差エントロピー誤差関数
・イテレーション
・エポック
以上が大項目「ディープラーニングの概要」の中の一つ「学習の最適化」の内容でした。
ディープラーニングに関しても、細かく学習しようとするとキリがありませんし、専門的過ぎて難しくなってきます。
そこで、強化学習と同じように「そこそこ」で理解し、あとは「そういうのもあるのね」くらいで理解するのがいいでしょう。
そこで以下のようなことが重要になってくるのではないかと。
・ディープラーニングの特徴(それぞれの手法はどんな特徴があるのか)
・それぞれの手法のアルゴリズム(数式を覚えるのではなく、何が行われているか)
・何に使用されているのか(有名なもののみ)
ディープラーニングは様々な手法があるので、この三つだけでも非常に大変です。
しかし、学習を進めていると有名なものは、何度も出てくるので覚えられるようになります。
後は、新しい技術を知っているかどうかになりますが、シラバスに載っているものを押さえておけば問題ないかと。
次回は「ディープラーニングの概要」の「学習の最適化」第二弾です。
覚える内容が多いですが、りけーこっとんも頑張ります!
ではまた~

続きは以下のページからどうぞ!











コメント